-
题目描述 :
- 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
- 请必须使用时间复杂度为
O(log n)的算法。

-
思路分析:
- 这段代码的解题思想是利用二分查找的方法在一个有序数组中寻找目标元素的索引或者确定目标元素应该插入的位置。二分查找的核心思想是通过比较目标元素与数组中间位置的元素的大小关系,从而缩小查找范围。在每一步中,根据中间元素与目标元素的大小关系,确定目标元素可能存在的区间,然后不断缩小这个区间范围,直到找到目标元素或确定插入位置为止。
- 通过不断将查找区间一分为二,每次比较都能将待查找元素所在的区间范围减半,从而快速定位目标元素的位置。这种分治的思想使得二分查找算法的时间复杂度为O(log n),相比线性查找具有更高的效率,特别是在大规模数据集中。因此,二分查找是一种高效的查找算法,适用于有序数组这样的情况。
-
解题步骤:
-
1.初始化左右指针:
-
初始化
left为0,表示数组的起始位置,right为数组的最后一个位置。
-
-
2.循环查找:
-
在 while 循环中,只要
left小于等于right,就继续查找。
-
-
3.计算中间位置:
-
计算中间位置
mid,通过(left + right) / 2获得。
-
-
4.比较目标值:
- 如果
nums[mid]等于目标值target,则找到目标元素,直接返回mid。 - 如果
nums[mid]小于目标值target,说明目标值在右侧,更新left = mid + 1。 - 如果
nums[mid]大于目标值target,说明目标值在左侧,更新right = mid - 1。
- 如果
-
5.返回插入位置:
-
当循环结束时,如果没有找到目标元素,则返回
left,表示应该插入的位置。
-
- 以下是完整代码:
-
class Solution {public int searchInsert(int[] nums, int target) {int left = 0;int right = nums.length - 1;while (left <= right) {int mid = left + (right - left) / 2;if (nums[mid] == target) {return mid;} else if (nums[mid] < target) {left = mid + 1;} else {right = mid - 1;}}return left;} } -
这一期的代码还是比较简单的, 但是可以注意一下小细节, 可以进一步优化代码
-
在这个二分查找算法中,当循环结束时,`left`指向的位置就是目标元素应该插入的位置。这是因为在循环中,`left`始终指向小于等于目标元素的位置,而`right`始终指向大于等于目标元素的位置。
当循环结束时,如果数组中存在目标元素,则会在某个位置`mid`找到它,返回该位置。如果数组中不存在目标元素,`left`将指向第一个大于目标元素的位置,也就是目标元素应该插入的位置。因此,直接返回`left`即可得到正确的插入位置。
这样的设计确保了无论目标元素是否存在于数组中,都能正确返回目标元素应该插入的位置,以保持数组的有序性。
-
-
-
搜索插入位置-java
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.hqwc.cn/news/573141.html
如若内容造成侵权/违法违规/事实不符,请联系编程知识网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
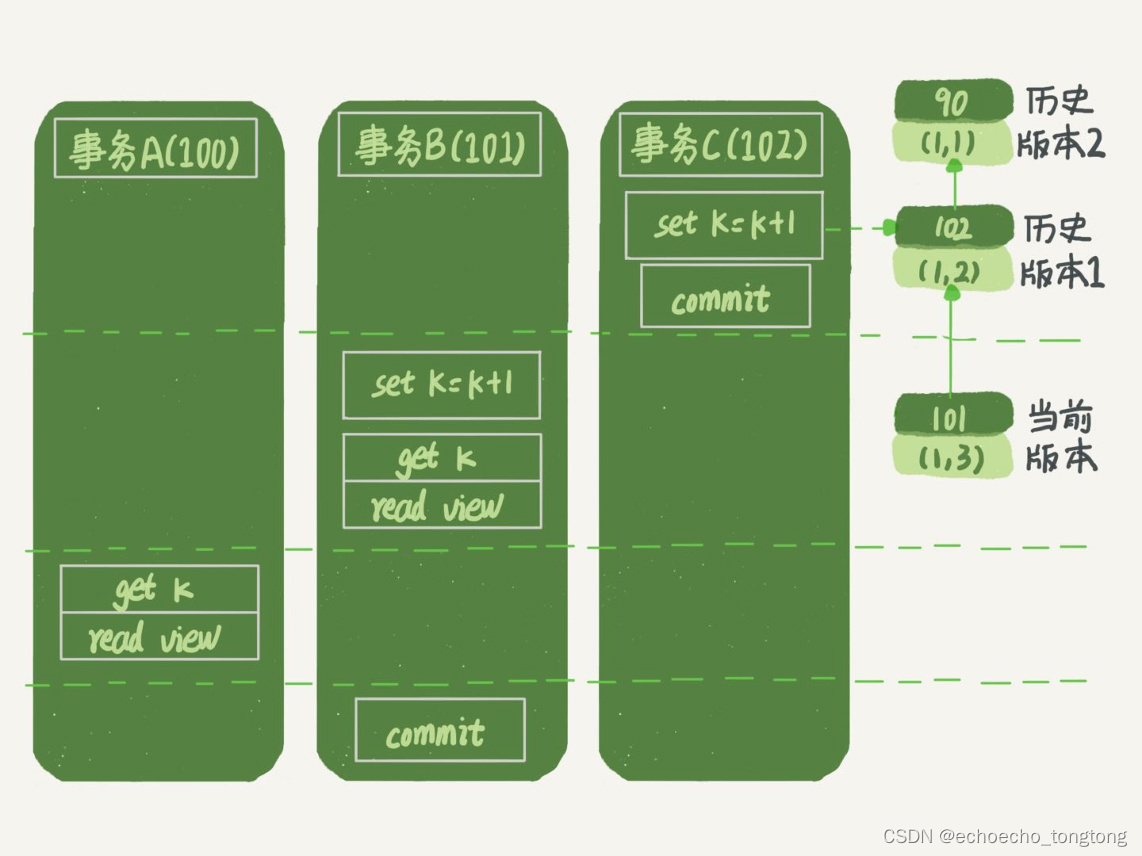
MySql实战--事务到底是隔离的还是不隔离的
第3篇文章和你讲事务隔离级别的时候提到过,如果是可重复读隔离级别,事务T启动的时候会创建一个视图read-view,之后事务T执行期间,即使有其他事务修改了数据,事务T看到的仍然跟在启动时看到的一样。也就是说,…
深入探讨分布式ID生成方案
🎈🎈作者主页: 喔的嘛呀🎈🎈 🎈🎈所属专栏:python爬虫学习🎈🎈 ✨✨谢谢大家捧场,祝屏幕前的小伙伴们每天都有好运相伴左右,一定要天天…
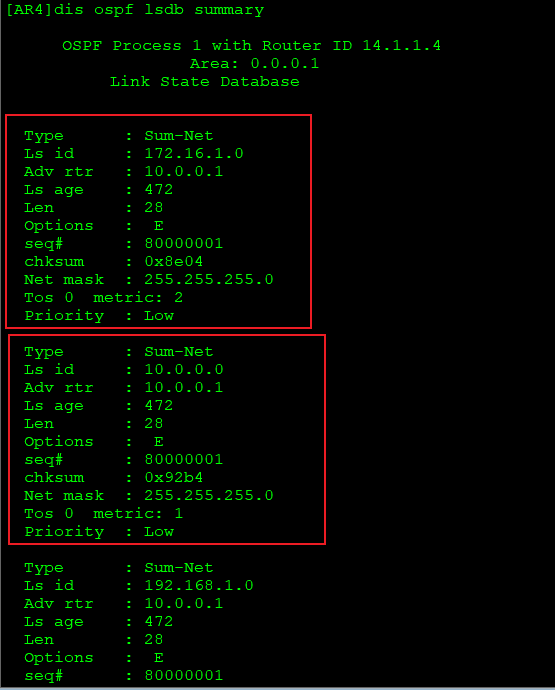
OSPF-区域间路由计算
一、概述 前面学习了我们学习了Router-LSA和Network-LSA,它们都只能在区域内进行泛洪,而且我们之前一直主要是单区域学习。OSPF的核心是骨干区域Area 0,其它都为非骨干区域。但是在大型网络中,单区域OSPF会存在一定的问题…
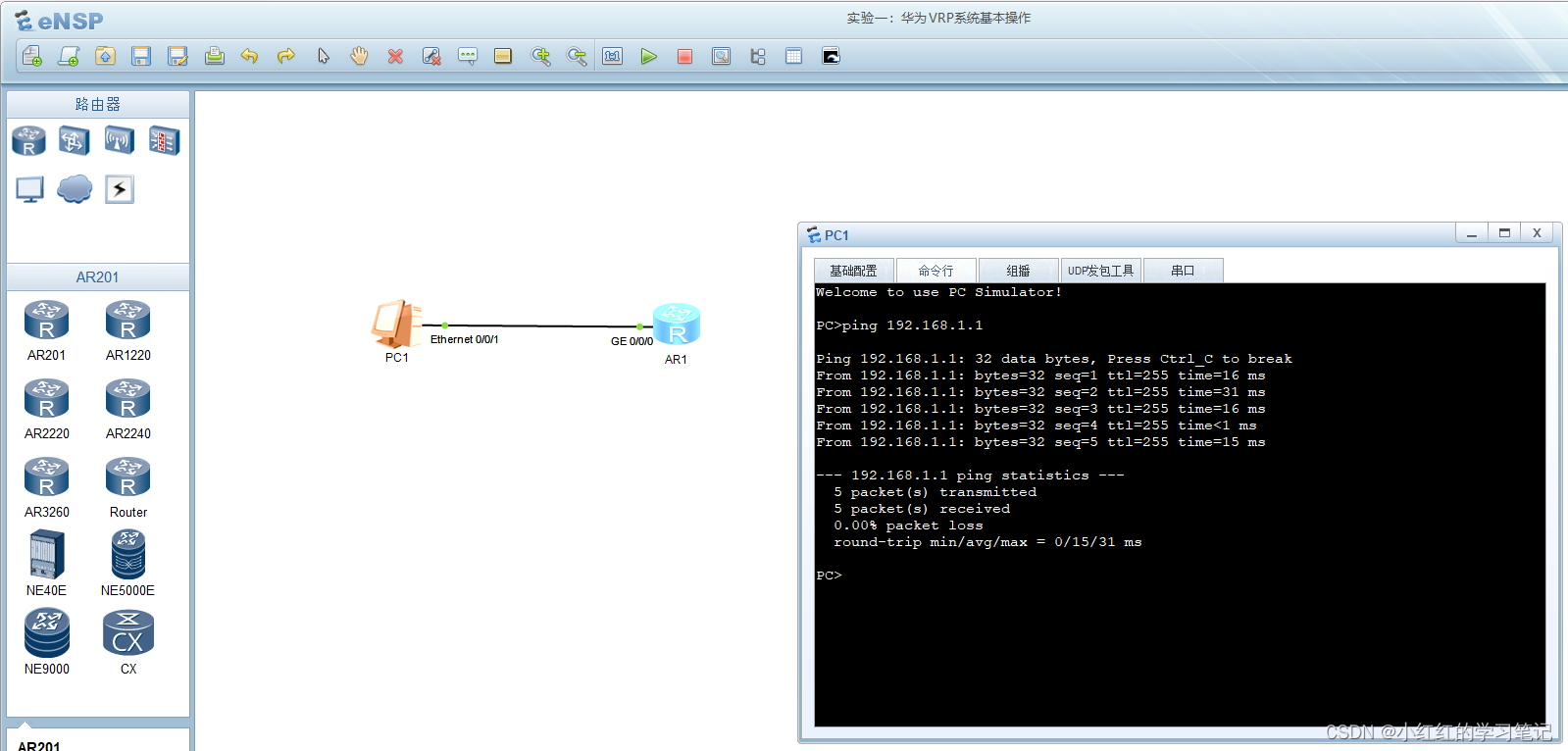
HCIA-Datacom实验_03_实验一:华为VRP系统基本操作
1.运行eNSP,设置-界面设置-自定义界面-设备标签,“总显示接口标签” 打钩。 2.按照实验拓扑添加设备 注:如果是真实环境,需要接两条线:
(1)串口线:电脑USB口到网络设备Console口&am…
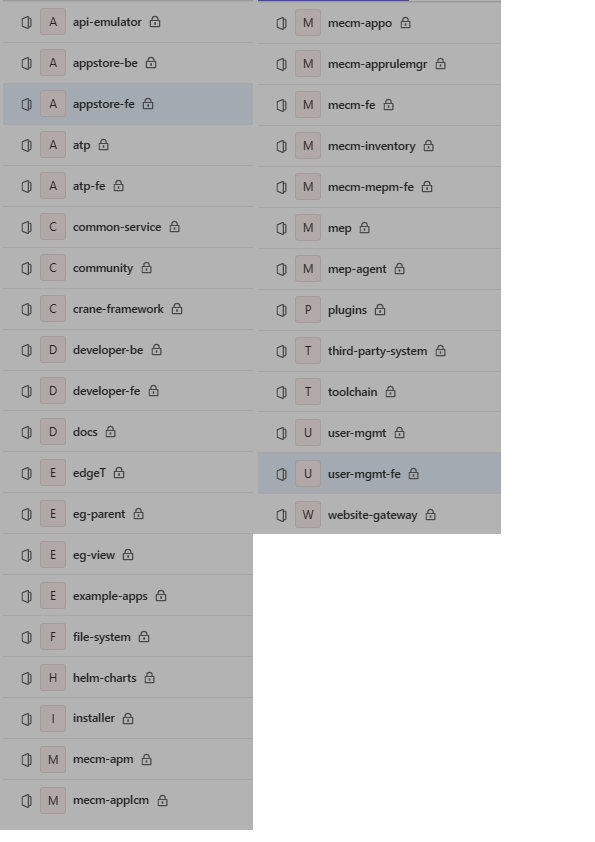
EdgeGallery开发指南
API接口
简介
EdgeGallery支持第三方业务系统通过北向接口网关调用EdgeGallery的业务接口。调用流程如下图所示(融合前端edgegallery-fe包含融合前端界面以及北向接口网关功能,通过浏览器访问时打开的是融合前端的界面,通过IP:Port/urlPref…
免费SSL证书和付费SSL证书的区别点
背景:
在了解免费SSL证书和付费SSL证书的区别之前,先带大家了解一下SSL证书的概念和作用。 SSL证书的概念:
SSL证书就是基于http超文本传输协议的延伸,在http访问的基础上增加了一个文本传输加密的协议,由于http是明…
第十篇【传奇开心果系列】Python自动化办公库技术点案例示例:深度解读Python自动化操作Excel
传奇开心果博文系列 系列博文目录Python自动化办公库技术点案例示例系列博文目录 前言一、重要作用解说二、Python操作Excel的常用库介绍三、数据处理和分析示例代码四、自动化报表生成示例代码五、数据导入和导出示例代码六、数据可视化示例代码八、数据校验和清洗示例代码九、…
【Java程序设计】【C00386】基于(JavaWeb)Springboot的校运会管理系统(有论文)
基于(JavaWeb)Springboot的校运会管理系统(有论文) 项目简介项目获取开发环境项目技术运行截图 博主介绍:java高级开发,从事互联网行业六年,已经做了六年的毕业设计程序开发,开发过上…
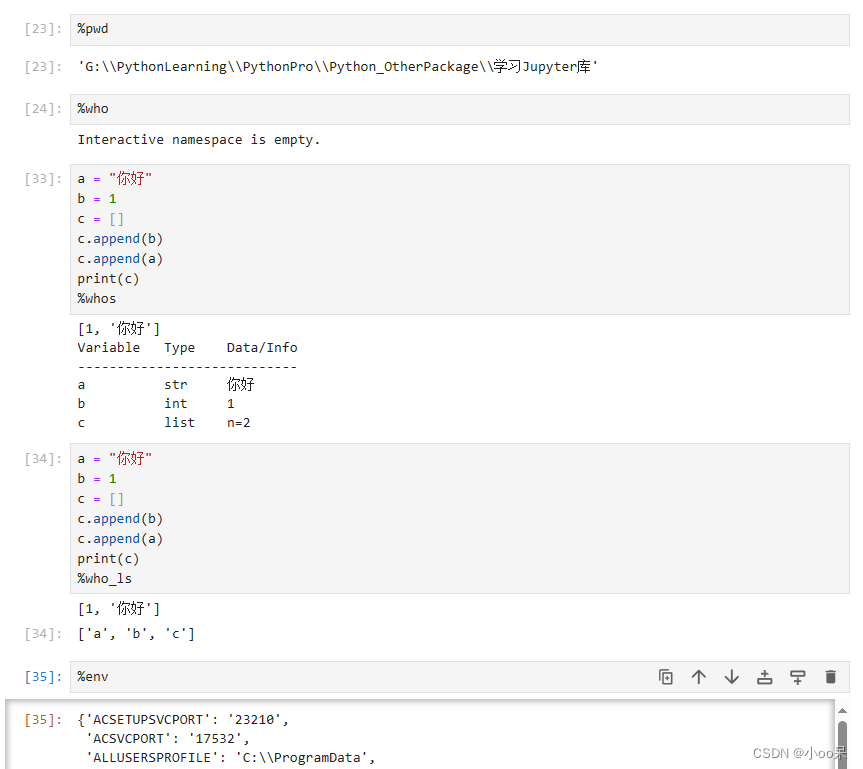
【学习心得】Jupyter常用操作与魔法方法
一、安装与打开
Jupyter是什么我就不啰嗦了,直接安装:
pip install jupyter 安装完后,在你想要打开的项目路径下,唤出CMD执行下面命令就可以使用jupyter notebook了
jupyter notebook 也可以用更加好用的jupyter lab࿰…
LabVIEW无人机大气数据智能测试系统
LabVIEW无人机大气数据智能测试系统
随着无人机技术的迅速发展,大气数据计算机作为重要的机载设备,在确保飞行安全性方面发挥着重要作用。设计了一套基于LabVIEW的无人机大气数据智能测试系统,通过高效、稳定的性能测试,及时发现…
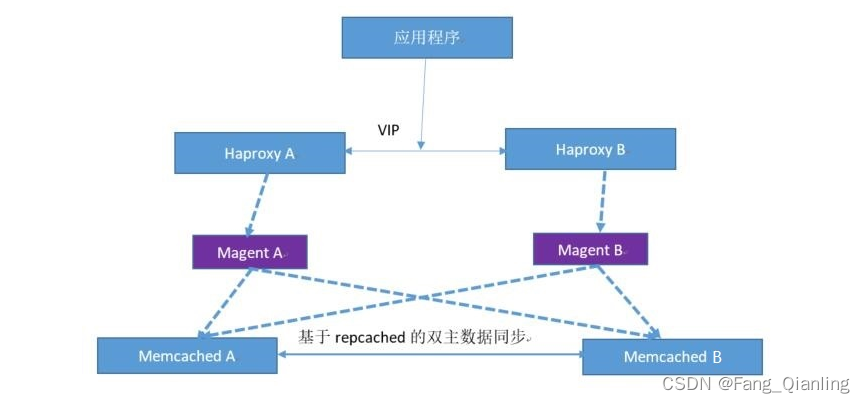
Memcached非关系型数据库介绍
使用背景
Memcached 不是一个数据库,而是一个高性能的分布式内存对象缓存系统。它主要用于减轻数据库负载,提高动态Web应用的速度、可扩展性和性能。Memcached 的工作原理是将数据存储在内存中,以提供快速的数据访问。当应用程序需要访问数据…
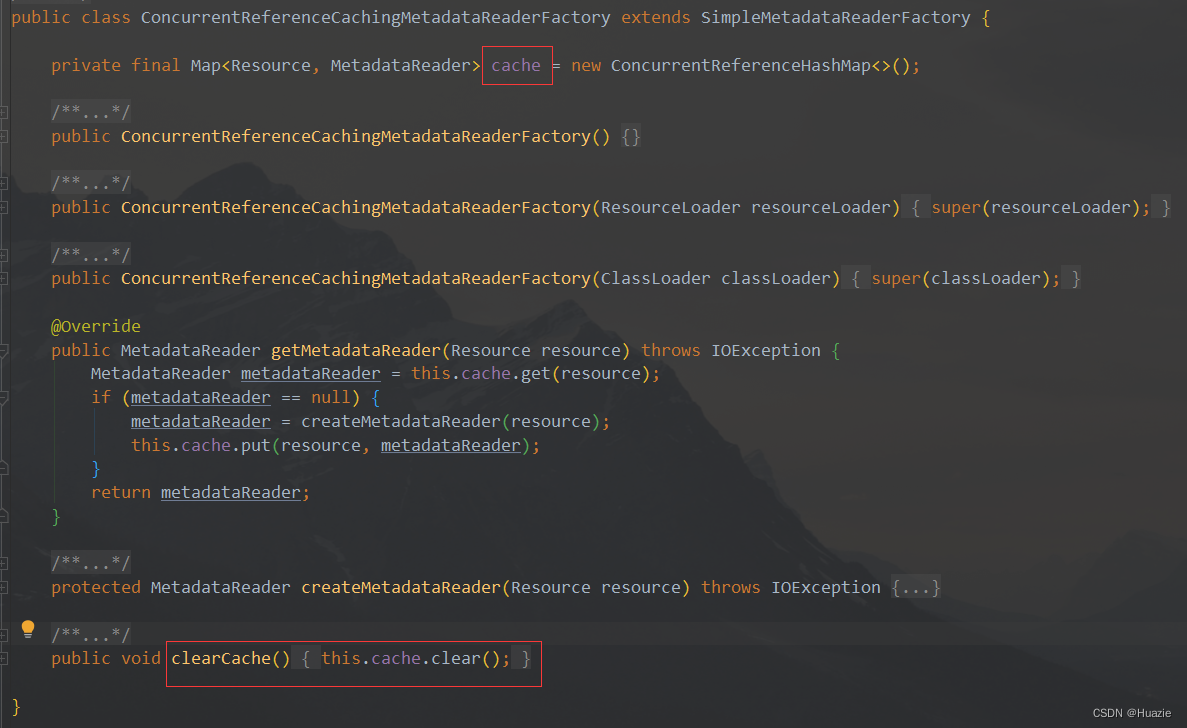
【Spring Boot 源码学习】共享 MetadataReaderFactory 上下文初始化器
《Spring Boot 源码学习系列》 共享 MetadataReaderFactory 上下文初始化器 一、引言二、往期内容三、主要内容3.1 源码初识3.2 CachingMetadataReaderFactoryPostProcessor3.2.1 register 方法3.2.1 configureConfigurationClassPostProcessor 方法 3.3 ConfigurationClassPos…