案例一:
请分析IEEE 754双精度浮点数规格化数的表示范围。
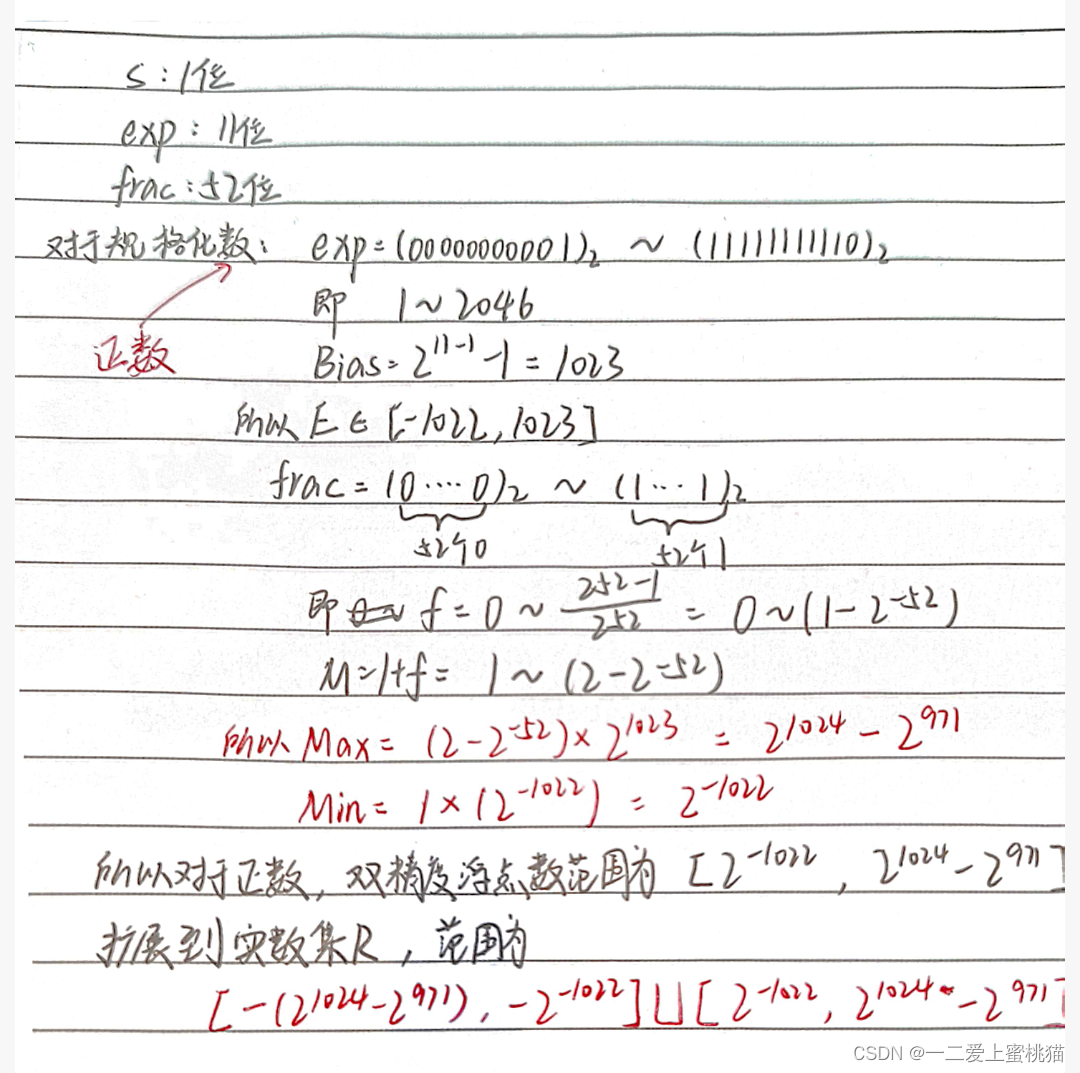
案例二:
规格化浮点数的Bias为什么采用2k-1-1而不是2k-1?非规范数的指数E=1-Bias而不是0-Bias?
(1)
① bias = 127时
E = e - 127 = (0000 0001,1111 1110)- 127=[-126,127]
这种情况下非规格化的 E = 1- bias = -126
②如果 bias = 128,则最终E = [-127, 126],非规格化E = 1- 128 = -127
③再或者 bias = 129、130等更大的数值,此时的最大值虽然很大,但是此时能表示的最小小数却很有限;或者 bias = 126、125等更小的数值,此时的最小值虽然很小,但是此时能表示的最大数也很有限。而bias = 12或者bias = 128时,确保了阶码能够对称地表示正指数和负指数。这使得阶码的范围在正负之间保持平衡,从而使浮点数的表示范围更优。
而且,比较bias等于127和128两种情况,我们可以发现,bias = 128比bias = 127多了一个2^(-127),但少了一个2^127,根据2^x函数和导函数图像来看,导数在x为正数时更大,且一阶导函数也是单调递增的,少一个2^(-127)似乎对数字表示影响并不大,但多了一个2^127却能使数字表示范围大了一倍,所以综上所述,bias=127更优,所以规格化浮点数的Bias采用2^(k-1)-1,而不是2^(k-1)。
(2)
E=1-Bias主要是为了使规格化数和非规格化数之间连续平稳过渡(有点类似于高数中函数连续的意味),如果换成0-Bias,则值为-127,与规格化数就间隔了-127到-126中间的部分,过渡就出现了缺口。


![[串联] MySQL 存储原理 B+树](https://img-blog.csdnimg.cn/img_convert/a861de68b3e4e335a78411b25d1e2d95.png)