在现实世界的机器学习应用中,通常有许多相关的特征,但只有其中的一个子集是可观察的。当处理有时可观察而有时不可观察的变量时,确实可以利用该变量可见或可观察的实例,以便学习和预测不可观察的实例。这种方法通常被称为处理缺失数据。通过使用变量可观察的可用实例,机器学习算法可以从观察到的数据中学习模式和关系。然后,这些学习到的模式可以用于预测变量在缺失或不可观察的情况下的值。
期望最大化算法可用于处理变量部分可观察的情况。当某些变量是可观察的时,我们可以使用这些实例来学习和估计它们的值。然后,我们可以预测这些变量在不可观测的情况下的值。
EM算法是在1977年由亚瑟·登普斯特、南·莱尔德和唐纳德·鲁宾发表的一篇开创性论文中提出并命名的。他们的工作形式化了算法,并证明了其在统计建模和估计中的实用性。
EM算法适用于潜变量,潜变量是不能直接观测到的变量,而是从其他观测变量的值推断出来的。通过利用控制这些潜在变量的概率分布的已知一般形式,EM算法可以预测它们的值。
EM算法是机器学习领域中许多无监督聚类算法的基础。它提供了一个框架来找到统计模型的局部最大似然参数,并在数据缺失或不完整的情况下推断潜在变量。
期望最大化算法
期望最大化(EM)算法是一种迭代优化方法,它结合了不同的无监督机器学习算法,以找到涉及未观察到的潜在变量的统计模型中参数的最大似然或最大后验估计。EM算法通常用于潜变量模型,可以处理缺失数据。它由估计步骤(E步骤)和最大化步骤(M步骤)组成,形成迭代过程以改善模型拟合。
- 在E步骤中,算法使用当前参数估计值计算潜在变量,即对数似然的期望值。
- 在M步骤中,算法确定使在E步骤中获得的期望对数似然最大化的参数,并且基于估计的潜在变量更新相应的模型参数。

通过迭代地重复这些步骤,EM算法寻求最大化观察数据的可能性。它通常用于无监督学习任务,例如聚类,其中隐变量被推断并在各种领域中应用,包括机器学习,计算机视觉和自然语言处理。
EM算法中的关键术语
期望最大化(EM)算法中最常用的一些关键术语如下:
- 潜在变量:潜变量是统计模型中不可观测的变量,只能通过其对可观测变量的影响间接推断。它们不能直接测量,但可以通过它们对可观察变量的影响来检测。
- 可能性:在给定模型参数的情况下,观察到给定数据的概率。在EM算法中,目标是找到使可能性最大化的参数。
- 对数似然函数:它是似然函数的对数,用于度量观测数据与模型之间的拟合优度。EM算法寻求最大化对数似然。
- 最大似然估计(Maximum Likewise Estimation,MLE):MLE是一种通过找到使似然函数最大化的参数值来估计统计模型参数的方法,该方法衡量模型解释观测数据的程度。
- 后验概率:在贝叶斯推理的背景下,EM算法可以扩展到估计最大后验(MAP)估计,其中参数的后验概率是基于先验分布和似然函数计算的。
- 预期(E)步骤:EM算法的E步骤计算给定观测数据和当前参数估计的潜在变量的期望值或后验概率。它涉及计算每个数据点的每个潜在变量的概率。
- 最大化(M)步骤:EM算法的M步通过最大化从E步获得的预期对数似然来更新参数估计值。它涉及找到优化似然函数的参数值,通常通过数值优化方法。
- 收敛:收敛是指EM算法达到稳定解的条件。它通常通过检查对数似然或参数估计值的变化是否低于预定义的阈值来确定。
期望最大化(EM)算法是如何工作的
期望最大化算法的本质是使用数据集的可用观测数据来估计缺失数据,然后使用该数据来更新参数的值。让我们详细了解EM算法。
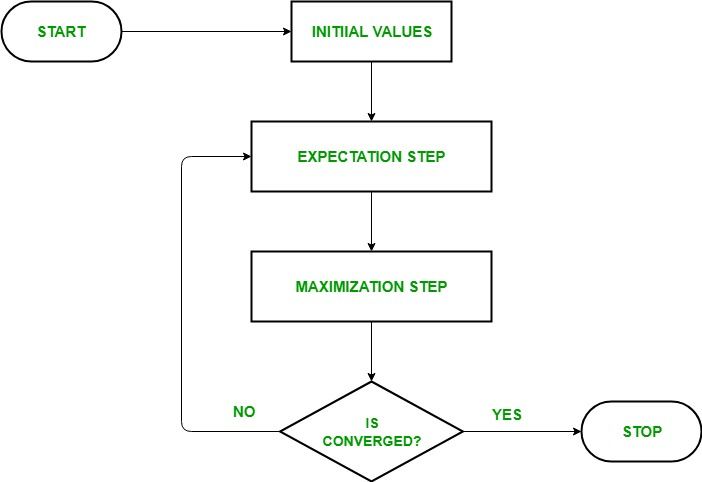
- 初始化:
首先,考虑一组参数的初始值。假设观测数据来自特定的模型,给系统一组不完整的观测数据。 - E-Step(期望步骤):在这一步中,我们使用观察到的数据来估计或猜测缺失或不完整数据的值。它主要用于更新变量。
在给定观测数据和当前参数估计值的情况下,计算每个潜在变量的后验概率。
使用当前参数估计值估计缺失或不完整的数据值。
基于当前参数估计值和估计缺失数据计算观测数据的对数似然。 - M步(最大化步骤):在这一步中,我们使用前面的“期望”步骤中生成的完整数据来更新参数值。它主要用于更新假设。
通过最大化从E步骤获得的预期完整数据对数似然来更新模型的参数。
这通常涉及解决优化问题,以找到最大化对数似然的参数值。
所使用的具体优化技术取决于问题的性质和所使用的模型。 - 融合:在该步骤中,检查值是否收敛,如果是,则停止,否则重复步骤2和步骤3,即“期望”步骤和“最大化”步骤,直到收敛发生。
通过比较迭代之间的对数似然或参数值的变化来检查收敛性。
如果变化低于预定义的阈值,则停止并认为算法收敛。
否则,返回E步骤并重复该过程,直到实现收敛。
期望最大化算法的实现
导入必要的库
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
生成具有两个高斯分量的数据集
# Generate a dataset with two Gaussian components
mu1, sigma1 = 2, 1
mu2, sigma2 = -1, 0.8
X1 = np.random.normal(mu1, sigma1, size=200)
X2 = np.random.normal(mu2, sigma2, size=600)
X = np.concatenate([X1, X2])# Plot the density estimation using seaborn
sns.kdeplot(X)
plt.xlabel('X')
plt.ylabel('Density')
plt.title('Density Estimation of X')
plt.show()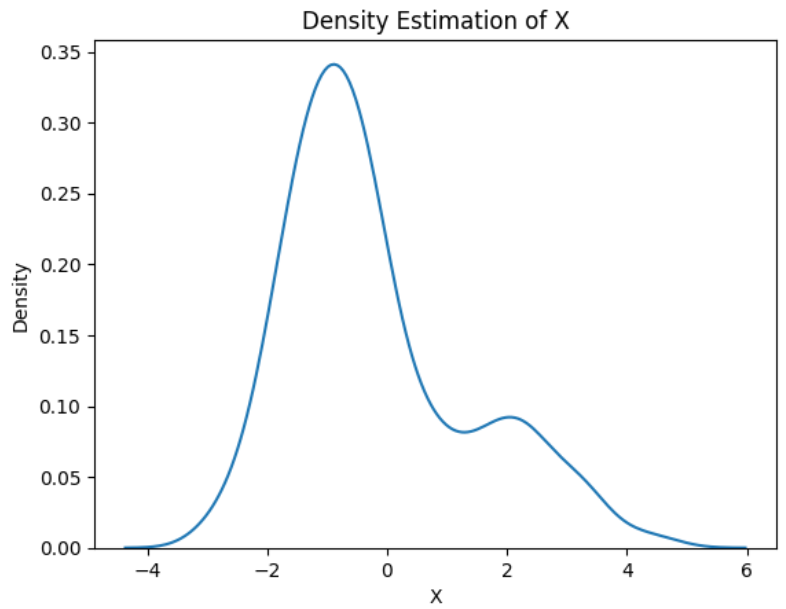
初始化参数
# Initialize parameters
mu1_hat, sigma1_hat = np.mean(X1), np.std(X1)
mu2_hat, sigma2_hat = np.mean(X2), np.std(X2)
pi1_hat, pi2_hat = len(X1) / len(X), len(X2) / len(X)执行EM算法
- 迭代指定数量的epoch(本例中为20)。
- 在每个epoch中,E步骤通过评估每个分量的高斯概率密度并通过相应的比例对其进行加权来计算(伽马值)。
- M步通过计算每个分量的加权平均值和标准差来更新参数。
# Perform EM algorithm for 20 epochs
num_epochs = 20
log_likelihoods = []for epoch in range(num_epochs):# E-step: Compute responsibilitiesgamma1 = pi1_hat * norm.pdf(X, mu1_hat, sigma1_hat)gamma2 = pi2_hat * norm.pdf(X, mu2_hat, sigma2_hat)total = gamma1 + gamma2gamma1 /= totalgamma2 /= total# M-step: Update parametersmu1_hat = np.sum(gamma1 * X) / np.sum(gamma1)mu2_hat = np.sum(gamma2 * X) / np.sum(gamma2)sigma1_hat = np.sqrt(np.sum(gamma1 * (X - mu1_hat)**2) / np.sum(gamma1))sigma2_hat = np.sqrt(np.sum(gamma2 * (X - mu2_hat)**2) / np.sum(gamma2))pi1_hat = np.mean(gamma1)pi2_hat = np.mean(gamma2)# Compute log-likelihoodlog_likelihood = np.sum(np.log(pi1_hat * norm.pdf(X, mu1_hat, sigma1_hat)+ pi2_hat * norm.pdf(X, mu2_hat, sigma2_hat)))log_likelihoods.append(log_likelihood)# Plot log-likelihood values over epochs
plt.plot(range(1, num_epochs+1), log_likelihoods)
plt.xlabel('Epoch')
plt.ylabel('Log-Likelihood')
plt.title('Log-Likelihood vs. Epoch')
plt.show()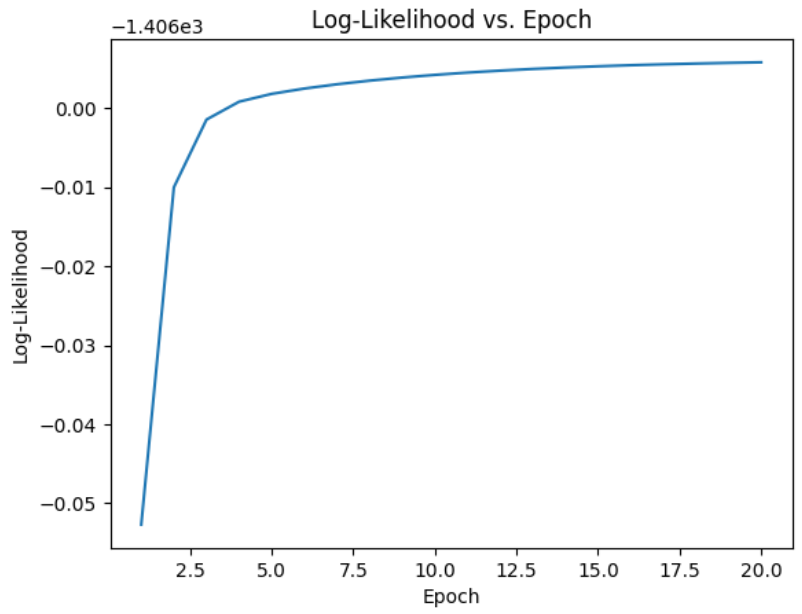
绘制最终密度估计
# Plot the final estimated density
X_sorted = np.sort(X)
density_estimation = pi1_hat*norm.pdf(X_sorted,mu1_hat, sigma1_hat) + pi2_hat * norm.pdf(X_sorted,mu2_hat, sigma2_hat)plt.plot(X_sorted, gaussian_kde(X_sorted)(X_sorted), color='green', linewidth=2)
plt.plot(X_sorted, density_estimation, color='red', linewidth=2)
plt.xlabel('X')
plt.ylabel('Density')
plt.title('Density Estimation of X')
plt.legend(['Kernel Density Estimation','Mixture Density'])
plt.show()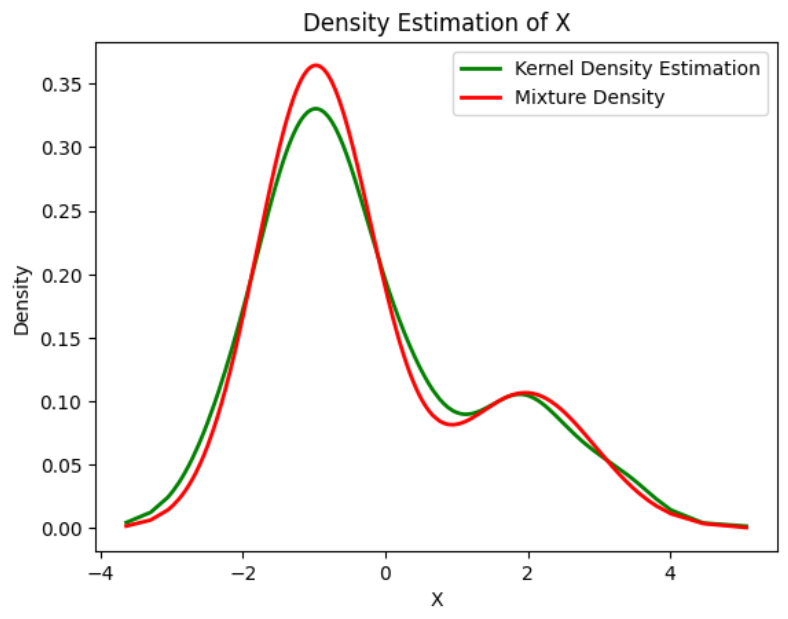
EM算法的应用
- 它可用于填充样本中缺失的数据
- 它可以作为无监督聚类学习的基础
- 它可以用于估计隐马尔可夫模型(HMM)的参数
- 它可以用来发现潜在变量的值
EM算法的优缺点
EM算法的优点
- 总是保证可能性将随着每次迭代而增加
- E步骤和M步骤在实现方面对于许多问题来说通常是相当容易的
- M阶的解通常以封闭形式存在
EM算法的缺点
- 它收敛缓慢
- 它只收敛到局部最优
- 它需要向前和向后的概率(数值优化只需要向前概率)
![[串联] MySQL 存储原理 B+树](https://img-blog.csdnimg.cn/img_convert/a861de68b3e4e335a78411b25d1e2d95.png)