力扣题目 509.斐波那契数

思路

• 很理所当然的，可以使用递归的方式
• 其次是用动态规划的方式，动态规划的核心就是递推公式。
  • 那么递推和递归一字之差，有什么区别呢？（递推和递归的区别）

1、递归

class Solution {//递归第一步：确定传入参数和返回值public int fib(int n) {//递归第二步：确定终止结果if(n == 0)return 0;if(n == 1)return 1;//递归第三步：确定单层递归的逻辑return fib(n-1) + fib(n-2);}
}

2、动态规划

动态规划五部曲：

1. 确定dp数组以及下标的含义——第i个数的斐波那契数值是dp【i】
2. 确定递推公式——dp【i】 = dp【i-1】+ dp【i-2】
3. dp数组的初始化——dp【0】 = 0；dp【1】=1；
4. 确定遍历顺序——从公式可以看出，数组dp的 i 依赖于前面的 i-1 和 i-2 ，所以从前往后顺序
5. 打印数组——就是我们自己来举例模拟debug自己的代码是否正确

//非压缩版本
class Solution {public int fib(int n) {int[] dp = new int[n+1];if(n <= 1){return n;}else{dp[0] = 0;dp[1] = 1;for(int i=2; i<=n; i++){dp[i] = dp[i-1] + dp[i-2];}}return dp[n];}
}

//压缩版本
class Solution {public int fib(int n) {//int[] dp = new int[n+1];if(n <= 1){return n;}else{//dp[0] = 0;//dp[1] = 1;int a=0, b=1, sum=0;    //可以理解为a是i-2，b是i-1，sum是ifor(int i=2; i<=n; i++){//dp[i] = dp[i-1] + dp[i-2];sum = a+b;a = b;b = sum;}return sum;}//return dp[n];}
}

---

力扣题目  746.使用最小花费爬楼梯

思路

1. dp数组的含义——到达i位置时，花费的体力dp【i】
2. 确定递推公式——因为 i 是由 i-1 或者 i-2 来得到的，所以 i = (i-1 + cost) 与 (i-2 + cost) 的最小的哪一个
3. 确定初始值——因为直接从该位置起来不用花费体力，dp1 = 0；dp0 = 0
4. 确定遍历顺序—— 因为 i 是由 i-1 或者 i-2  推理出来的，所以由前往后遍历
5. 打印数组

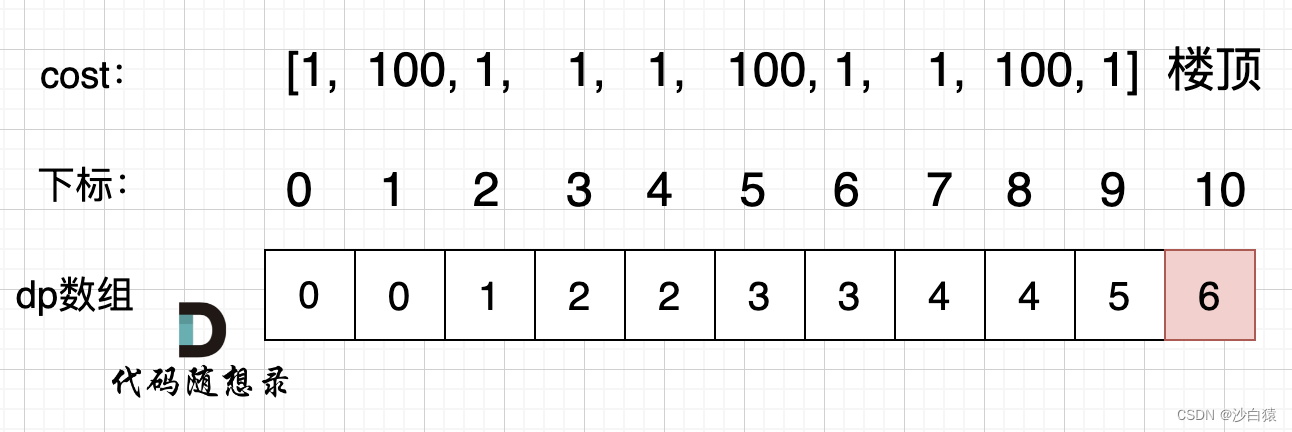
class Solution {public int minCostClimbingStairs(int[] cost) {int length = cost.length;int[] dp = new int [length + 1];    //这里+1是因为这个下标才是楼顶//因为第一步直接从0或1开始，不用花费dp[0] = 0;dp[1] = 0;//由提示可以看出，楼顶至少是下标为2for(int i=2; i <= length; i++){dp[i] = Math.min(dp[i-1] + cost[i-1],dp[i-2] + cost[i-2]);}return dp[length];}
}