论文题目：A Hybrid Path Planning Method Based on Improved A∗ and CSA-APF Algorithms

1 摘要

大问题：复杂动态环境下全局路径规划难以避开动态障碍物，且局部路径容易陷入局部最优的问题

• 问题1：针对A*算法产生冗余路径节点和非光滑路径
  解决方案：引入加权启发函数、去除冗余路径节点和引入三次准均匀B-样条曲线等改进措施，提高搜索速度，生成更光滑的路径。
• 问题2：针对APF算法存在的目标点不可达和易陷入局部最优的问题
  解决方案：
  （1）通过引入机器人到目标点的相对距离的m次幂来修改排斥势场函数，以确保可达性
  （2）另一方面，介绍了CSA-APF（增广势场约束模拟退火）算法，该算法将APF算法与模拟退火算法相结合，结合角度和安全距离约束，以避免局部最优，并产生全局最优点。

通过不同场景下的仿真实验对所提出的方法进行了比较。实验结果表明，该方法能有效地实现复杂动态环境下的路径规划。

2 Introduction

基于启发式搜索的A*算法能够快速规划出最短路径，而基于力场的APF算法能够动态避障。本文针对机器人路径规划算法中存在的问题，提出了一种改进的混合路径规划方法，以提高机器人在复杂环境下的路径规划性能。

本文的贡献：
（1）通过改进启发式函数提高了算法的搜索速度。采用消除冗余路径节点的策略，减少路径的长度，并集成三阶准均匀B样条曲线，增强路径的光顺性
（2）通过改进基于机器人到目标点相对距离的m次幂的排斥势场函数，对APF算法进行优化，解决了目标点不可达的问题。此外，提出了CSA-APF算法，该算法在模拟退火算法的基础上引入了角度和距离安全约束。这种增强限制了全局最优点的搜索空间，并集成了改进的模拟退火算法来生成全局最优目标点。这指导APF算法克服局部最优问题，同时规划平滑和安全的路径。
（3）将改进的A*算法与CSA-APF算法相结合，提高了机器人的自主导航性能。为移动的机器人的路径规划提供了一种有效可行的解决方案。

3 全局路径规划算法的改进

3.1 改进启发式函数

为了提高路径搜索的速度而不牺牲显著的准确性，本文对启发式函数进行加权调整，使搜索速度由快速过渡到正常。改进的启发式函数表示如下：
$$f(n)=g(n)+\left(1+\frac{h^2(n)}{e^{h(n)}}\right)h(n)$$

3.2 消除冗余路径节点的策略

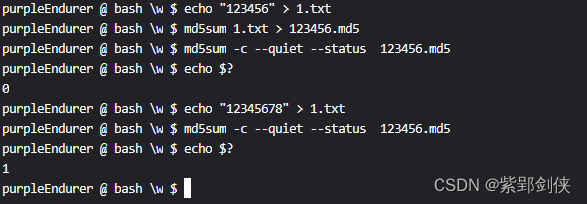
采用一种策略来消除路径中的冗余节点，从而减少路径中的转弯点数量，从而规划出一条转弯点少、转弯角小的无碰撞路径。

(1) 获取节点矩阵[N1;N2;…;Nn]：表示A*算法的初始规划路径，表示为N，其中N1是起始点，Nn是目标点。创建一个新的矩阵K来存储关键路径节点，并将起始点和目标点添加到K矩阵中；
(2) 初始化变量：定义一个变量i作为矩阵N的指数，1≤i≤n，设置i=1
(3) 检查端点：创建一个While循环，当i + 2 > n时结束，其中i递增;
(4) 更新变量：从矩阵N的初始节点N1开始，依次从矩阵N中取出Ni、Ni+1、Ni+2三个节点;
(5) 共线性检查：计算线段NiNi+1和Ni+1 Ni +2的斜率，确定这两条线是否相等。如果斜率不相等，表明节点Ni、Ni+1和Ni +2不共线，则进行步骤6。否则，从矩阵N中删除节点Ni+1，更新N矩阵（n）的长度，返回步骤3;
(6) 障碍物检查：获取八个相邻网格单元中的节点Ni、Ni+1和Ni +2周围的障碍物，并将其存储在矩阵O中。连接线段Ni Ni +1，通过计算障碍物到线段Ni+1 Ni +2的距离，确定是否存在障碍物。如果存在障碍物，则将中间节点Ni+1识别为关键节点，将其添加到矩阵P，并设置i = i + 1，进入步骤3。否则删除节点Ni+1,更新n值，返回步骤3;
(7) 循环完成。剔除冗余节点后输出矩阵P，依次连接矩阵P的关键节点，得到优化路径。

3.3 道路的平滑

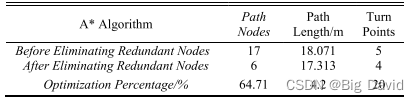
本文中，三次准均匀B样条曲线用于路径光顺。这种方法确保平滑路径紧密跟随原始路径，从而提高机器人的安全性和避障能力。

利用矩阵P存储的关键路径节点，通过A*的算法，确定了三次非均匀B样条曲线的控制点的基本方程组。

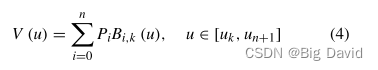
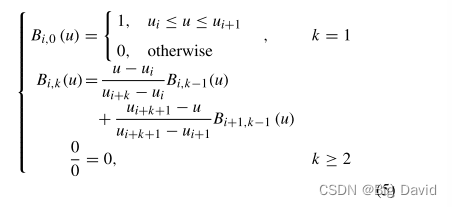
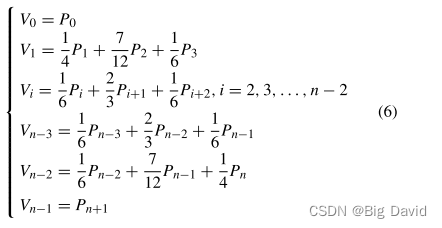
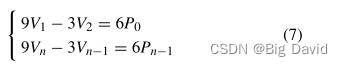
4 改进的局部路径规划算法

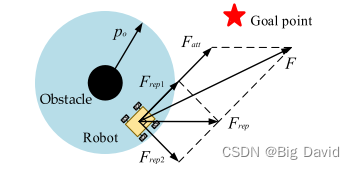
4.1 改进的排斥势场函数

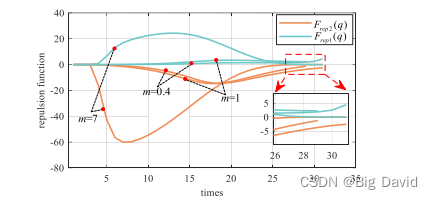
针对机器人可能会遇到由于排斥力而无法到达目标的问题。修改排斥函数，加入到目标的相对距离的m次方。该修改旨在减少排斥力分量并增加吸引力分量，从而解决该问题。

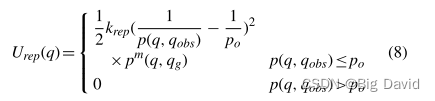
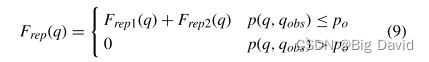
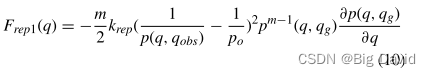
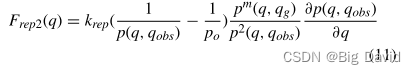
4.2 CSA-APF算法

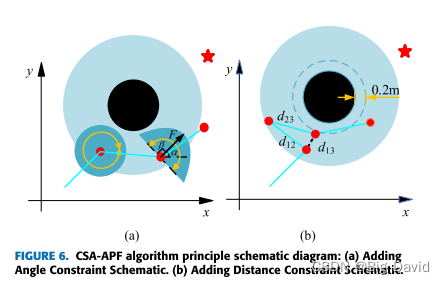
针对在某些情况下，当排斥力和吸引力之间的平衡可能导致机器人被卡在特定位置时，会出现局部最小值的问题，从而阻止其向目标前进的问题，引入虚拟目标点来引导人工势场算法跳出局部最优。另外，人工势场算法中引入虚拟目标点时，可能会产生不均匀的力，导致规划路径出现振荡和弯曲，因此需要进一步优化虚拟目标点的选取策略，以保证目标附近势场的力平衡。
将附加约束条件的SA算法与APF算法结合生成全局最优解的具体步骤如下：

(1) 以合力为零或机器人作往复运动为判据，判断APF算法是否陷入局部极小值;
(2) 如果陷入局部最小值问题，则删除局部最小值中的点，将前一点设置为当前点，并调用SA算法进行优化。否则，继续使用APF算法;
(3) 将当前路径点设置为随机矩阵的起始点，为初始温度和最终温度;
(4) 生成一个随机点，计算A点和B点的总势能;
(5) 计算势场差
(6) 根据▲U的大小，决定是否接受B点。如果▲U< 0，则接受点B;否则，根据大都会准则，以一定概率接受点E或生成新的随机点C;
(7) 如果阈值|Uk − Uk−1|> γ和γ满足，退出循环;否则，返回步骤4。随着不断迭代，温度逐渐降低，接受替代点的概率降低，并最终朝着最佳点F方向收敛。

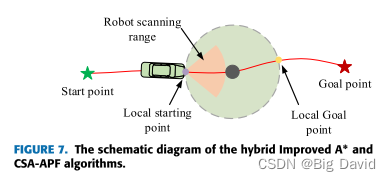
5 路径规划的混合算法实现

首先，构建网格环境地图，设定路径的起点和终点，在已知环境地图信息的基础上，采用改进的A*算法进行全局路径规划。

其次，传输机器人当前位置，并基于传感器信息实时感知周围地图环境信息。考虑到地图环境中存在多个动态障碍物的可能性，当在机器人的扫描范围内检测到动态障碍物时，需要确定该动态障碍物是否是最后一个。如果是最后一个动态障碍物，则检查动态障碍物的排斥范围内是否有目标点。如果存在目标点，则将其设置为局部目标点;否则，将距离全局路径大于或等于机器人扫描半径的点设置为局部目标点。

然后，调用CSA-APF算法进行局部路径规划。如果不是最后一个动态障碍物，则继续检查相邻的动态障碍物。如果存在相邻障碍物，则向后遍历，直到没有相邻的动态障碍物。如果最后一个障碍物也是相邻障碍物，则使用与上述相同的方法确定局部目标点并执行局部路径规划。如果没有相邻障碍物，则调用局部路径规划算法。如果机器人的扫描范围内没有动态障碍物，则按照A*算法规划的路径进行。

最后，重复上述步骤，直到机器人到达目标点。

6 实验结果

实验使用了联想军团R9000P笔记本电脑，配备了AMD锐龙7 5800H处理器和NVIDIA GeForce RTX3060显卡。实验平台采用Matlab 2021b.以下概述了实验的具体验证过程：
A.一种改进的MATLAB算法仿真实验

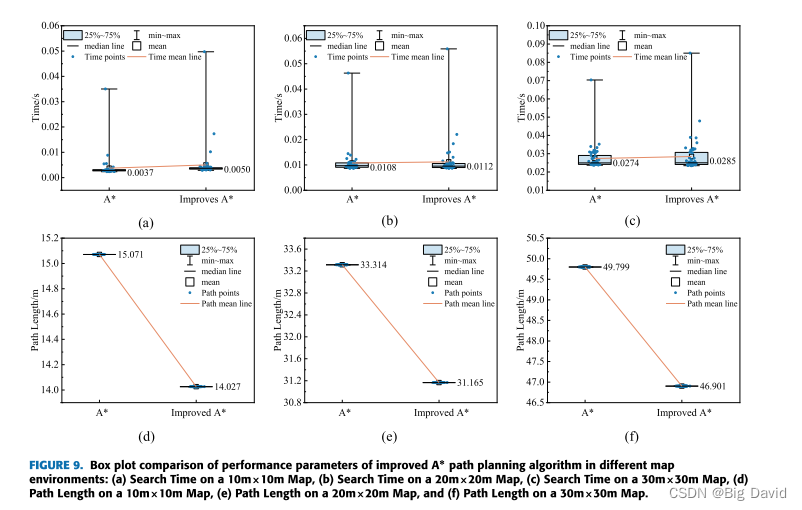
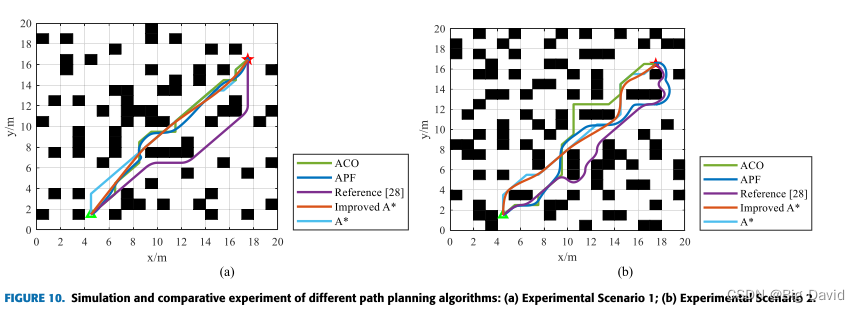
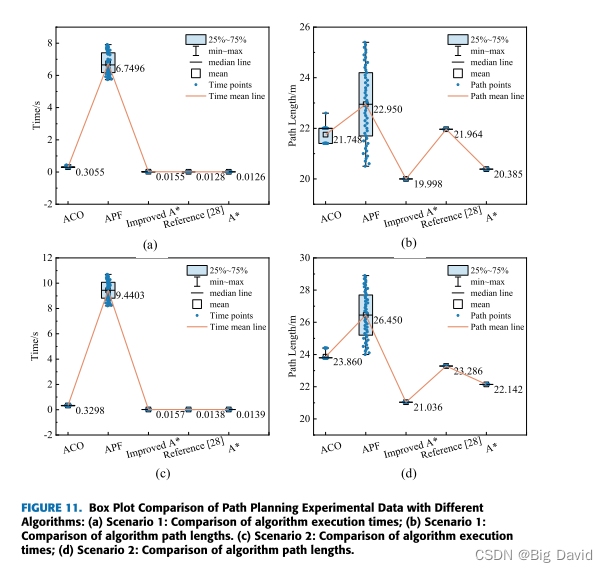
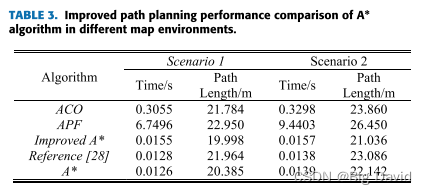
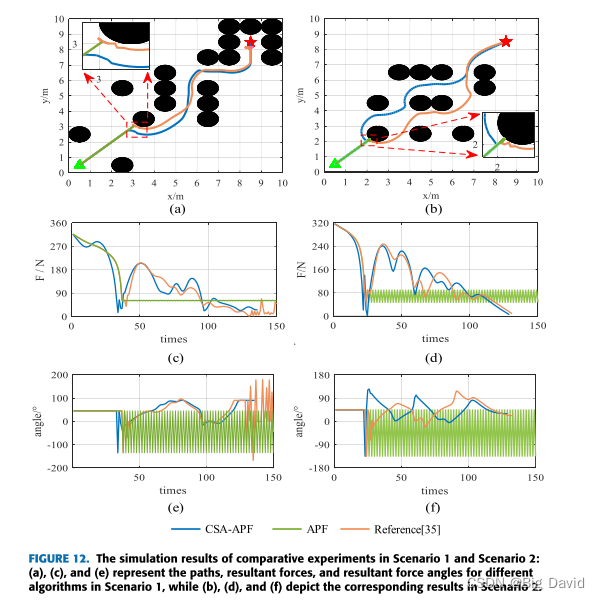
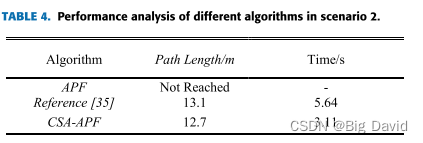
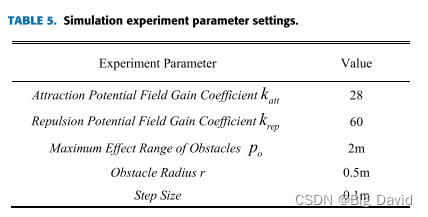
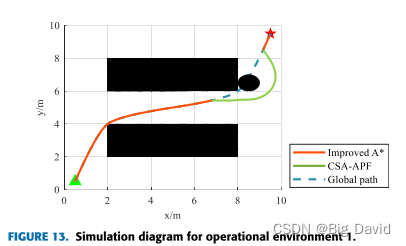
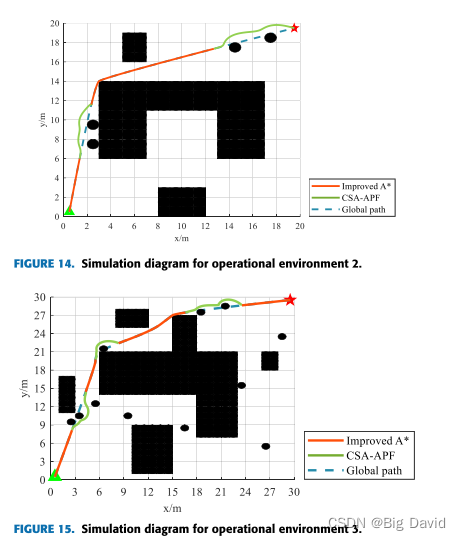
7 结论

针对复杂动态环境下的路径规划问题，提出了一种结合改进的A*算法和CSA-APF算法的混合路径规划方法。目标是使机器人能够规划全局最优路径，同时有效地执行动态避障任务。

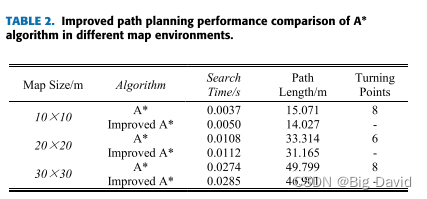
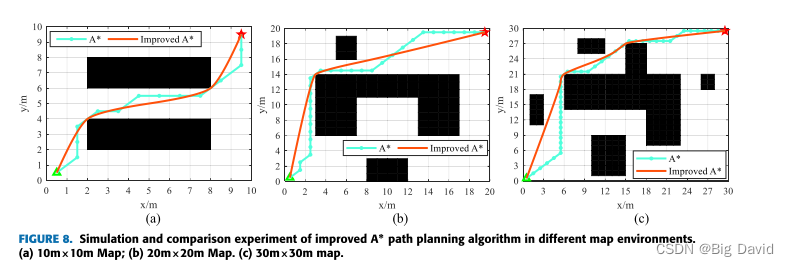
在全局路径规划部分，通过优化启发函数、消除冗余节点和引入三阶准均匀B样条曲线，成功地解决了A-样条算法在路径规划方面的不足。仿真结果表明，改进算法减少了路径中不必要的转弯点，使路径长度减少了5.82%~ 6.93%。在局部路径规划方面，CSA-APF算法通过改进排斥势场函数来实现目标可达性。此外，通过将模拟退火算法与附加角度和安全距离约束相结合，CSA-APF有效地克服了传统APF算法的局限性。各种环境下的实验结果表明，CSA-APF使移动的机器人能够安全地通过障碍物，保证了路径规划的平滑性和连续性。与对比算法相比，CSA-APF路径长度缩短了3%，路径搜索时间减少了44.86%。最后，结合动态和静态障碍物环境，对改进的A-均值滤波算法和CSA-APF算法进行了仿真实验。结果表明，该混合算法成功地解决了在全局路径规划中避免动态障碍和防止局部路径陷入次优解的挑战。这为实际应用中机器人的平稳运动提供了有效的支持。