计算机网络——数据链路层(差错控制)
- 差错从何而来
- 数据链路层的差错控制
- 检错编码
- 奇偶校验码
- 循环冗余校验(CRC)
- FCS
- 纠错编码
- 海明码
- 海明距离
- 纠错流程
- 确定校验码的位数r
- 确定校验码和数据位置
- 求出校验码的值
- 检错并纠错
我们今年天来继续学习计算机网络数据链路层这一小节的内容,我们今天主要来看数据链路层中关于数据控制与纠错——差错控制。
差错从何而来
计算机网络中数据链路层出现的差错主要来源于以下几个方面:
- 噪声:
- 全局性噪声:这类噪声源于通信信道自身的电气特性,如随机热噪声,这是由于导体内部电子的热运动导致的,这种噪声具有随机性和持续性,是信道固有属性,难以完全避免。为了减少此类噪声的影响,通常采取提高信噪比的方法,例如使用更好的物理介质、增强信号强度或采用更先进的信号处理技术。
- 局部性噪声:这类噪声是由于外部环境中的短暂事件引起,如电磁干扰(EMI)、闪电、电源波动或其他瞬态现象产生的冲击噪声。这类噪声往往突发性强,可能会导致短时间内大量数据位发生错误。针对这类噪声,常通过使用各种编码技术来进行差错检测和纠正,比如循环冗余校验(CRC)、前向纠错码(FEC)等。
- 硬件故障:包括但不限于电缆破损、接头松动、接口失效、传输设备老化等问题,这些都可能导致信号失真或错误。
- 信号衰减与畸变:随着信号在传输过程中的距离增加,其振幅、频率和相位可能逐渐衰减或发生改变,特别是在长距离传输和无线传输时,这种现象更为显著,从而导致接收端解码出错。
- 多径效应:对于无线通信而言,信号可能经过多个路径到达接收端,各个路径的信号相互叠加,可能会引入差错。
同时差错的分类:
在计算机网络中,数据链路层可能出现的差错大致可以分为以下几类:
- 单比特错误(Single-Bit Error):
这是最基本的错误类型,指在数据传输过程中,单个比特(bit)由于噪声或者其他原因发生了反转,即1变成了0或者0变成了1。
- 多比特错误(Multiple-Bit Error):
指在一个数据单元内(如一个字节、一个码字)同时有两个或更多比特发生了错误。
- 突发错误(Burst Error):
在数据流中相邻的一段比特序列中出现连续的错误。突发错误经常由传输通道中的突发噪声或信号暂时失去同步等原因造成。
- 帧丢失(Frame Loss):
整个数据帧在传输过程中未能成功到达接收端,可能是由于严重的信号干扰、硬件故障或网络拥塞等原因导致。
- 帧重复(Frame Duplication):
同一数据帧在传输过程中被意外地重复发送多次。
- 帧乱序(Frame Misordering):
序列传输的数据帧在接收端收到了正确的帧,但它们的顺序与发送时的顺序不一致。
- 数据位滑动(Bit Slipping):
在同步传输系统中,如果接收端与发送端的时钟频率稍有差异,可能会导致接收端采样点发生偏移,进而产生位滑动错误。
差错控制技术设计时会根据不同的错误类型选择合适的检错和纠错编码方案,例如奇偶校验、循环冗余校验(CRC)用于检测单比特或多比特错误,而更复杂的编码如卷积码、级联码、交织码和海明码等可以用来检测并纠正突发错误。对于帧丢失、重复和乱序问题,则需要依靠协议栈中的相关机制进行管理,如序列号、确认应答、超时重传等手段。
综上所述,数据链路层在设计差错控制机制时,需要考虑到这些潜在的错误来源,并通过适当的编码、检错和纠错算法以及重传策略来保证数据的正确传输。
数据链路层的差错控制
数据链路层的差错控制主要包括以下几个方面的技术和方法:
- 检错编码:
奇偶校验:通过对数据添加额外的校验位,使得所有位数的总和是奇数或偶数,接收方可以通过重新计算校验和来判断是否有错误。
循环冗余校验(CRC):是一种更强大的检错方法,它通过附加一个冗余码(CRC码)到原始数据块后面,然后通过数学算法在接收端验证CRC值是否相符,以此来检测帧中的错误。
- 纠错编码:
前向纠错(FEC):通过使用特殊的编码技术(如Hamming码、BCH码、RS码、Turbo码或LDPC码等),不仅可以检测错误,还可以在一定范围内纠正错误,无需等待重传。
检错编码
奇偶校验码
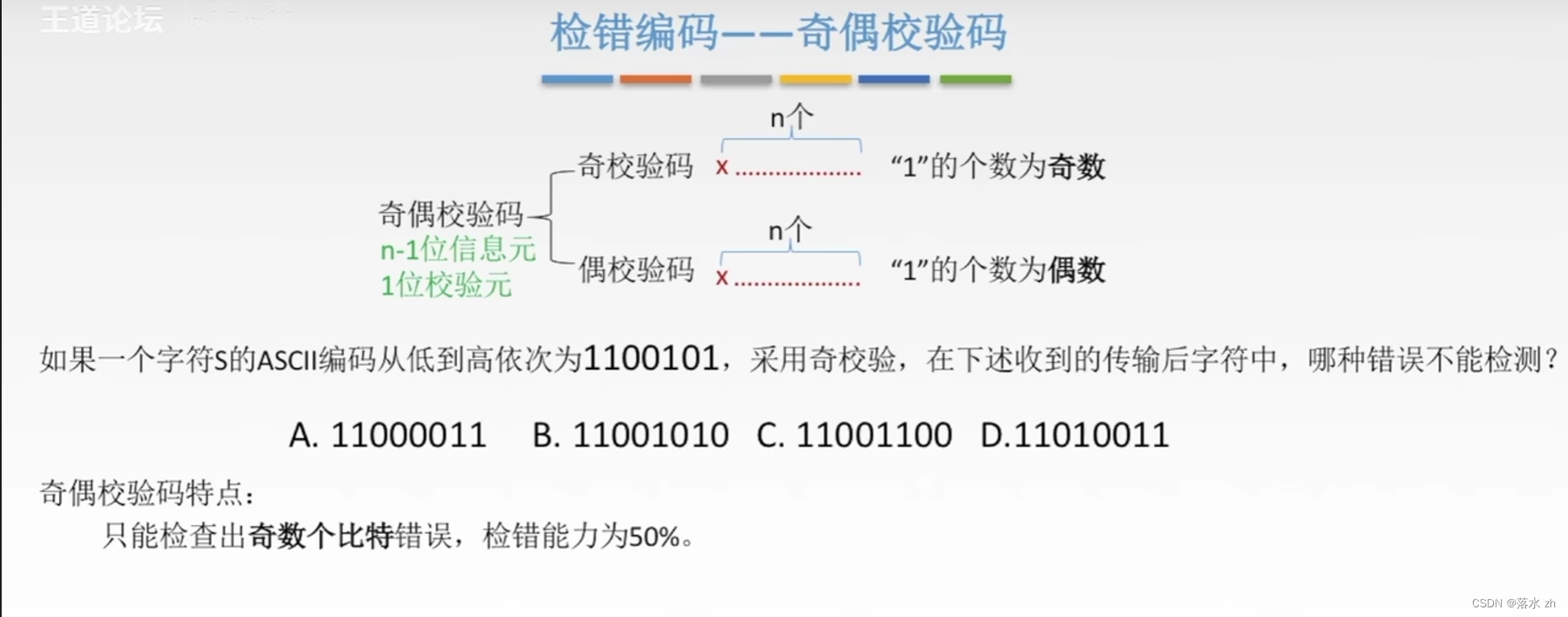
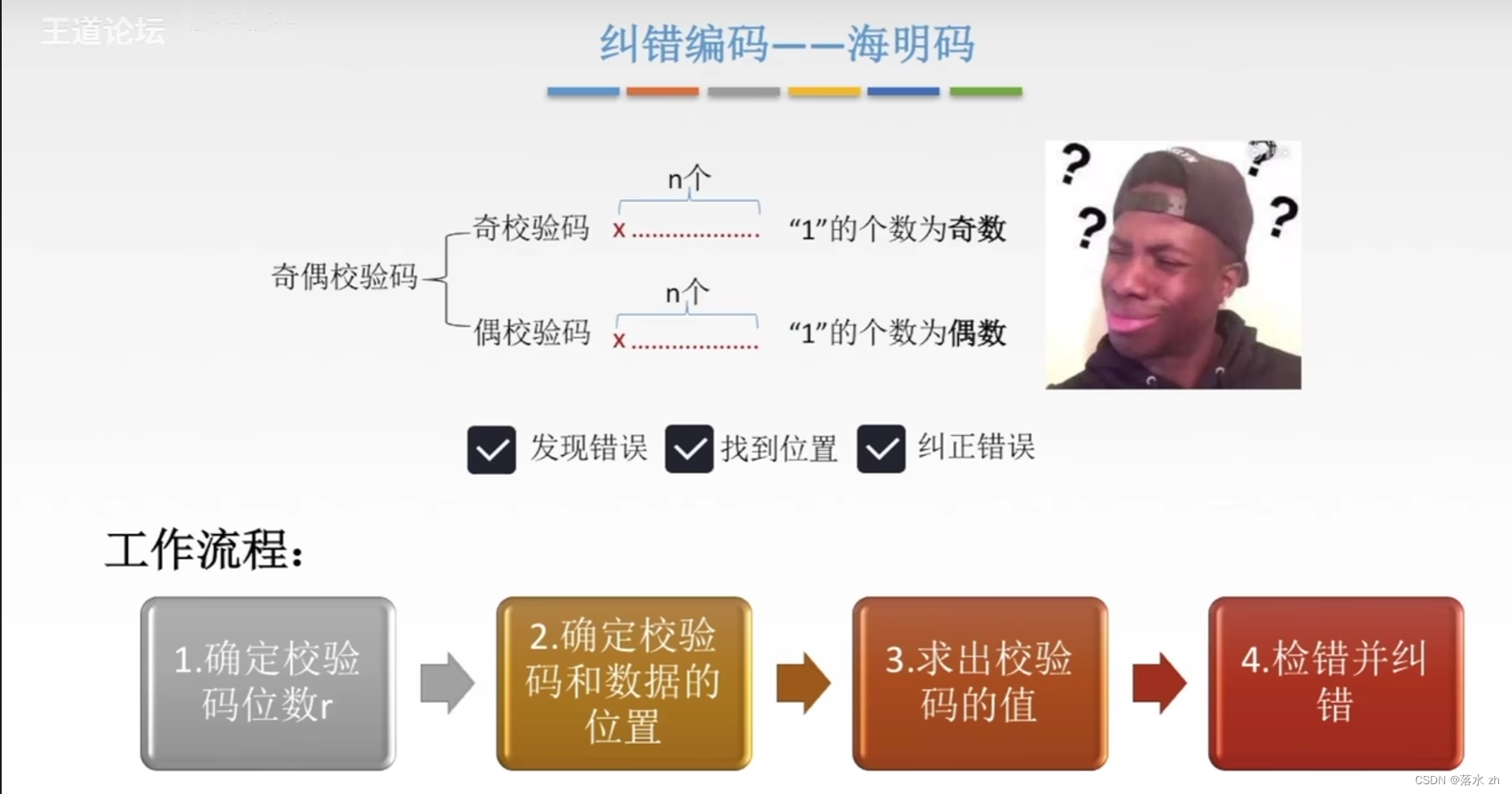
奇偶校验码(Parity Check Code)是一种简单的错误检测编码方法,主要用于在数据传输或存储过程中检测数据的完整性。奇偶校验码通过在原始数据位之后或之中增加一个校验位(也称为奇偶校验位),使得包含校验位在内的所有“1”的个数要么是奇数(奇校验),要么是偶数(偶校验)。
具体来说:
- 奇校验:如果原始数据位中“1”的个数是偶数,则校验位设置为“1”,使得整个数据块(原始数据位+校验位)中“1”的总数成为奇数。如果原始数据位中“1”的个数已经是奇数,则校验位设为“0”。
- 偶校验:与此相反,若原始数据位中“1”的个数是奇数,则校验位设为“1”以保证总“1”的个数为偶数;若原始数据位中“1”的个数已经是偶数,则校验位设为“0”。
奇偶校验码的主要优点在于实现简单,占用资源少。然而,它也有明显的局限性:
- 它只能检测出单个比特错误,也就是说,如果数据在传输过程中恰好只有一位发生变化,那么奇偶校验可以在接收端检测出这一错误。
- 当传输过程中出现两个或两个以上的比特错误时,奇偶校验可能无法检测出来,因为它无法区分单比特错误和多比特错误对“1”的总数的影响。
举一个例子:
假设我们有一个8位的数据串 “1010 0110”,现在我们要给这个数据串添加一个奇校验位,以确保整个数据块中"1"的个数为奇数。
首先,我们需要计算当前8位数据中"1"的个数。在这个例子中,共有4个"1"。由于我们想要的是奇数个"1",而现在已经有偶数个"1"(4个),所以我们需要在最后添加一个"1"作为奇校验位。于是,加上奇校验位后的完整数据串就变成了 “1010 0110 1”。
在数据接收端,对于带有奇校验位的数据串 “1010 0110 1” 的奇偶校验检查步骤如下:
接收端收到完整的数据帧后,将奇校验位与原始8位数据合并考虑。
计算整个数据帧(包括原始数据位和奇偶校验位)中 “1” 的个数。
根据奇校验的原则,如果计算得出的 “1” 的个数是奇数,则认为校验通过,数据没有发生错误。
如果计算得出的 “1” 的个数是偶数,则意味着数据在传输过程中可能发生了错误,因为按照奇校验规则,应该是一个奇数个 “1”,但现在却成了偶数个。
在这个例子中,接收端计算 “1010 0110 1” 中 “1” 的个数,发现共有5个 “1”,满足奇校验的要求,因此校验结果表明数据正确传输,无误。
对于奇偶校验码,只能检测单位出错,而不能检测多位出错的原因如下:
假设我们有一个4位的数据字1011,并决定使用偶校验。为了保持1的总数为偶数(或奇数,取决于我们选择的是偶校验还是奇校验),我们需要在数据后面添加一个校验位。在这个例子中,数据字中已经有3个1了(奇数个),所以我们需要添加一个1作为校验位,使得1的总数变为偶数。
原始数据字:1011
添加偶校验位后(假设校验位加在末尾):10111(此时1的个数为4,是偶数,满足偶校验的要求)
现在,假设在传输过程中发生了两位错误,数据变为了11011。如果我们用偶校验来检查这个数据:11011中1的个数仍然是4,是偶数,满足偶校验的要求。因此,从偶校验的角度来看,这个数据似乎是正确的。但是,实际上它包含了两位错误。这就是奇偶校验码不能检测多位错误的原因。它只能告诉我们数据中1的总数是奇数还是偶数,而不能告诉我们错误的具体位置或数量。
为了检测多位错误,我们需要使用更复杂的校验方法,如循环冗余校验(CRC)等。这些方法通过添加更多的校验位和使用更复杂的算法来提供更强大的错误检测能力。
循环冗余校验(CRC)
循环冗余校验(Cyclic Redundancy Check, CRC)是一种广泛应用在数据通信和存储系统中的错误检测编码技术。相较于简单的奇偶校验,CRC提供了更强的错误检测能力,尤其适用于检测并定位突发错误。
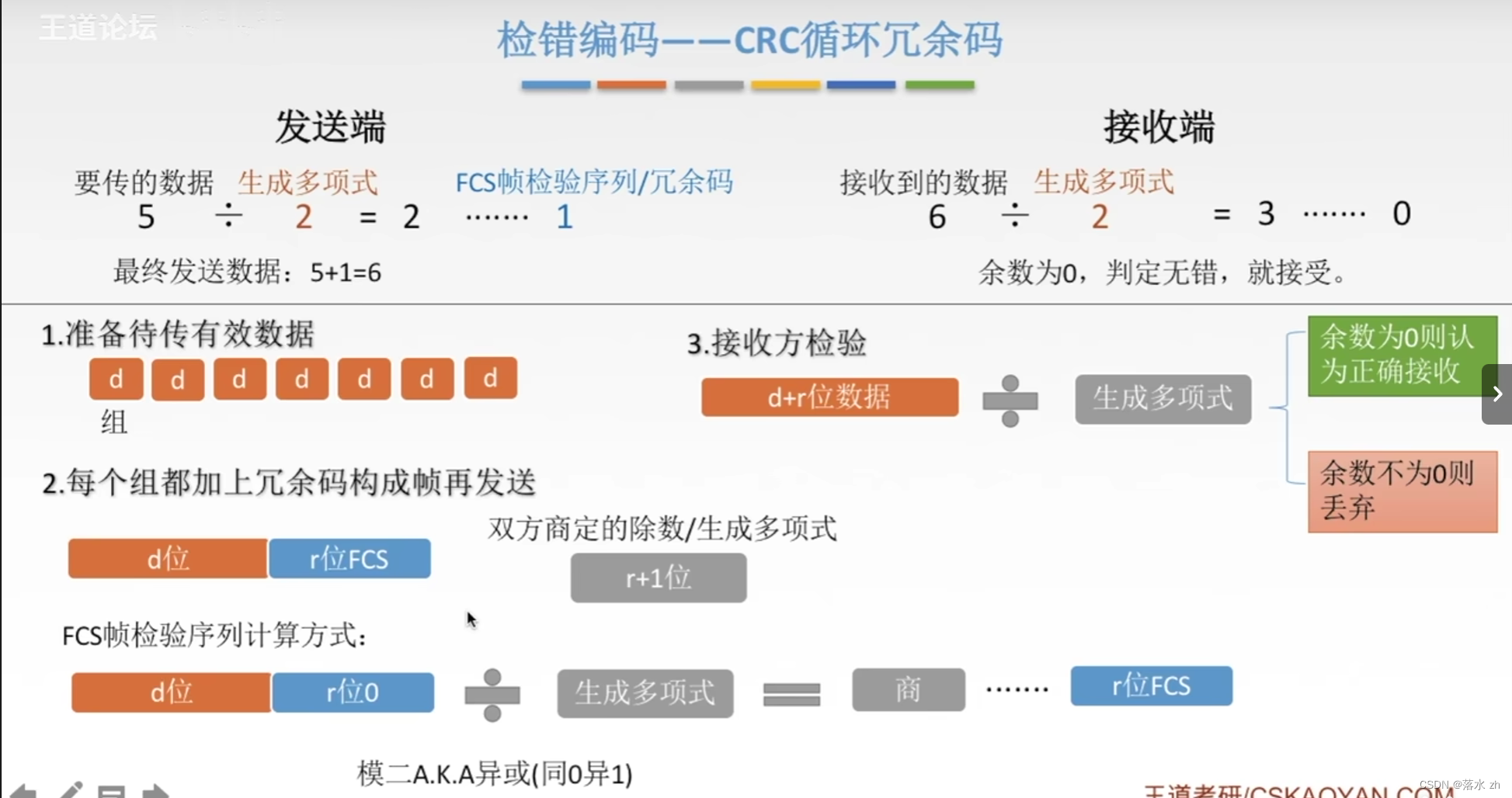
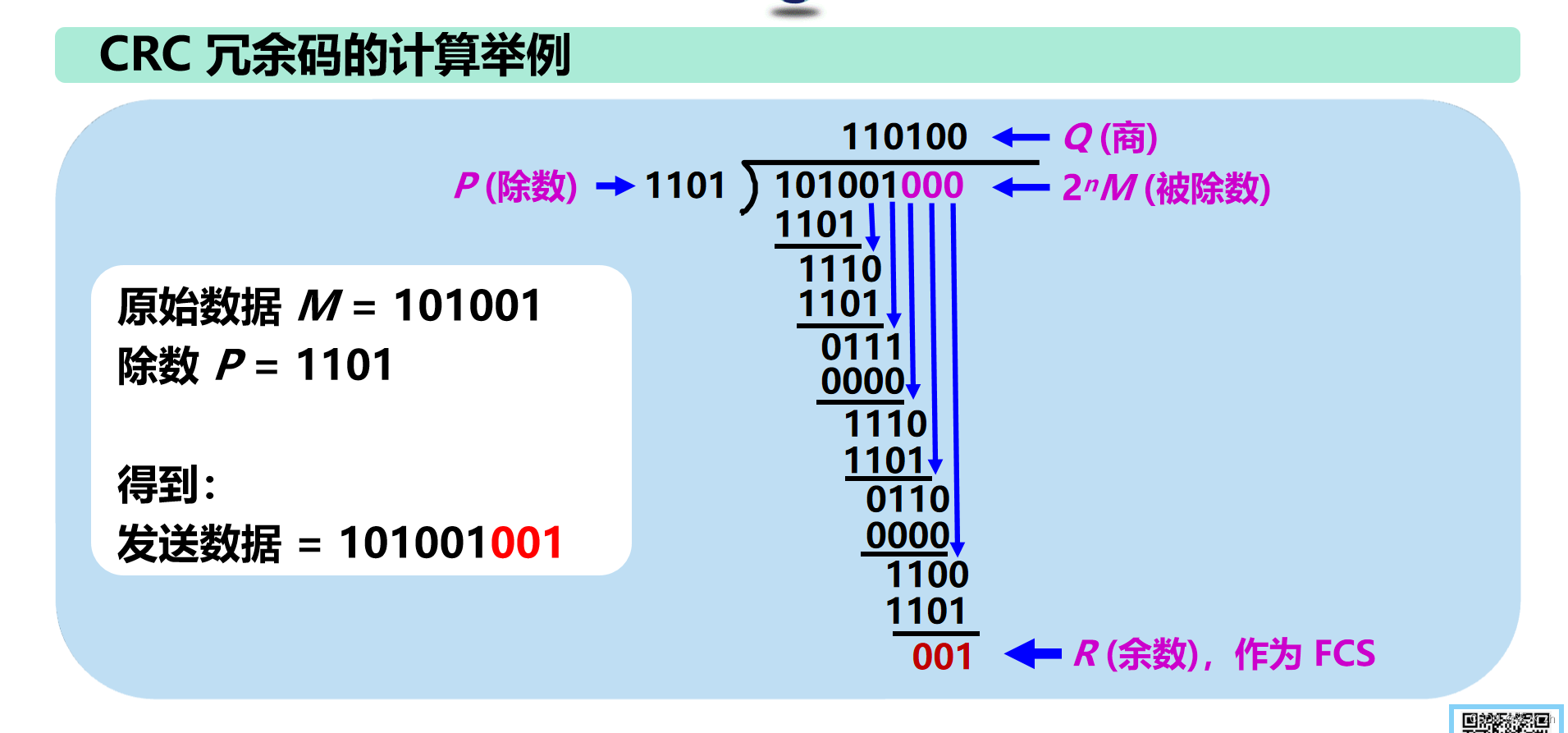
CRC工作原理的核心是利用一个预先定义好的多项式(称为生成多项式)对数据进行模2除法操作,生成一个固定长度的校验码(CRC码),并将这个校验码附加到数据块的末尾。当数据在传输过程中可能发生错误时,接收端重新计算接收到的数据块的CRC校验码,并与接收到的校验码进行比较。如果两者相符,则认为数据传输正确;如果不符,则表示数据在传输过程中出现了错误。
具体步骤如下:
- 初始化CRC寄存器:选择一个预设长度的二进制寄存器(通常是16位或32位),并填充初始值(通常是全1或全0)。
- 数据位处理:将待校验的数据从最高位到最低位逐位(或按指定字节顺序)与CRC寄存器内的值进行异或(XOR)操作,然后将结果向左移一位(相当于模2除法中的除法操作)。
- 除法运算:每次左移后,如果最高位是1,则还需要与生成多项式的二进制表示进行异或(相当于模2除法的减法步骤),直到所有的数据位都被处理完。
- 得到CRC校验码:最终留在CRC寄存器内的数值即为CRC校验码,将其添加至原始数据的末尾。
- 接收端校验:接收端收到带有CRC校验码的数据块后,独立地对该数据块重新计算CRC校验码,并与收到的CRC校验码进行对比,若二者相同则表示数据传输无误。
CRC的一个关键特性是其能够检测到多位错误,而且在特定条件下还能一定程度上检测到突发错误。不同的CRC算法使用的生成多项式不同,每种生成多项式对应着不同的CRC校验标准,如CRC-16、CRC-32等。这些标准因其在数据安全和效率上的平衡而广受青睐。

FCS
上面还有一个概念FCS:
FCS(Frame Check Sequence)是指帧校验序列,它是数据链路层用于错误检测的一种方法,类似于CRC(循环冗余校验)。FCS通常被包含在一个数据帧的尾部,作为该帧数据完整性和准确性的校验码。
在数据链路层协议中,如以太网Ethernet、HDLC(高级数据链路控制)、PPP(点对点协议)等,FCS都是必不可少的一部分。发送方会在每个数据帧后面附加上根据特定算法计算出的FCS,接收方在接收到整个帧后会重新计算FCS并与接收到的FCS进行比较。如果两者一致,则表明该帧在传输过程中没有发生错误或者错误在纠错范围内;如果不一致,则说明数据帧在传输过程中可能受到了损坏,接收方可能会丢弃该帧。
FCS的具体计算方法可以采用多种错误检测算法,其中CRC算法是最常用的实现方式之一。在以太网中,FCS就是基于CRC-32算法计算得出的32位校验值,而在PPP协议中,既可以使用CRC-16也可以使用其他类型的FCS算法。
举个栗子:
但是注意一下:

纠错编码
海明码
海明码(Hamming Code)是由美国科学家理查德·卫斯里·海明(Richard W. Hamming)于1950年发明的一种线性纠错码。海明码是一种能够同时检测并纠正单个比特错误的编码方法,特别适用于存储和通信领域,以提高数据的可靠性。
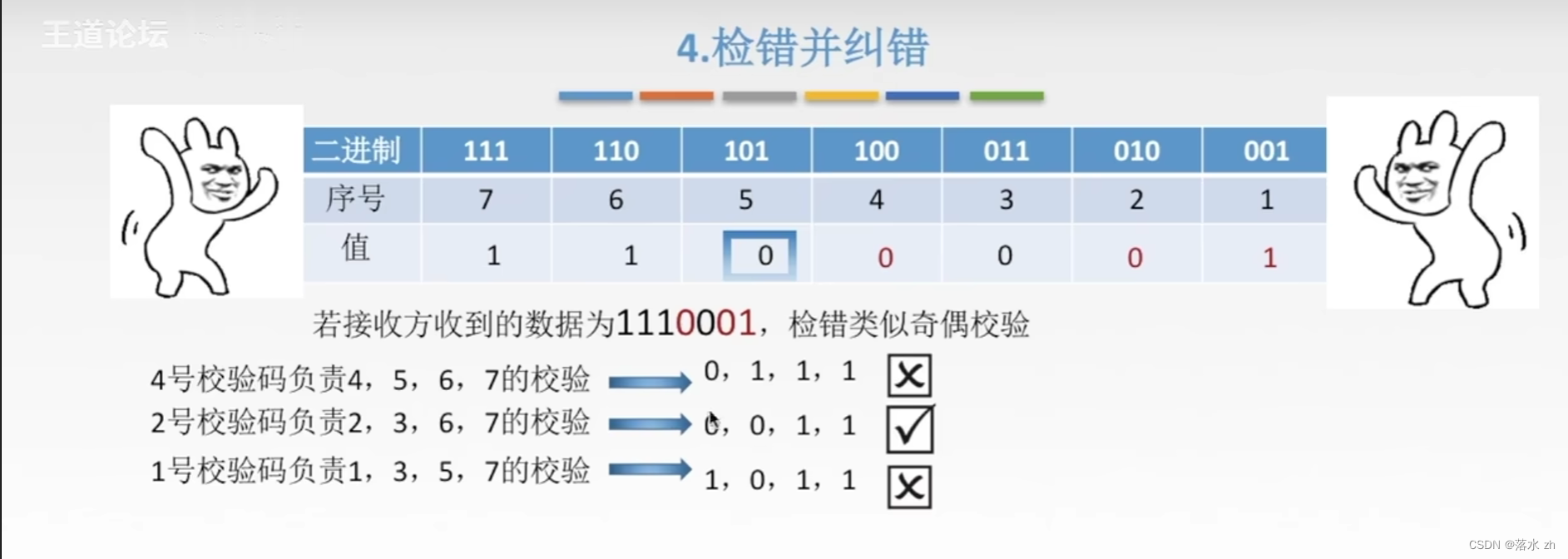
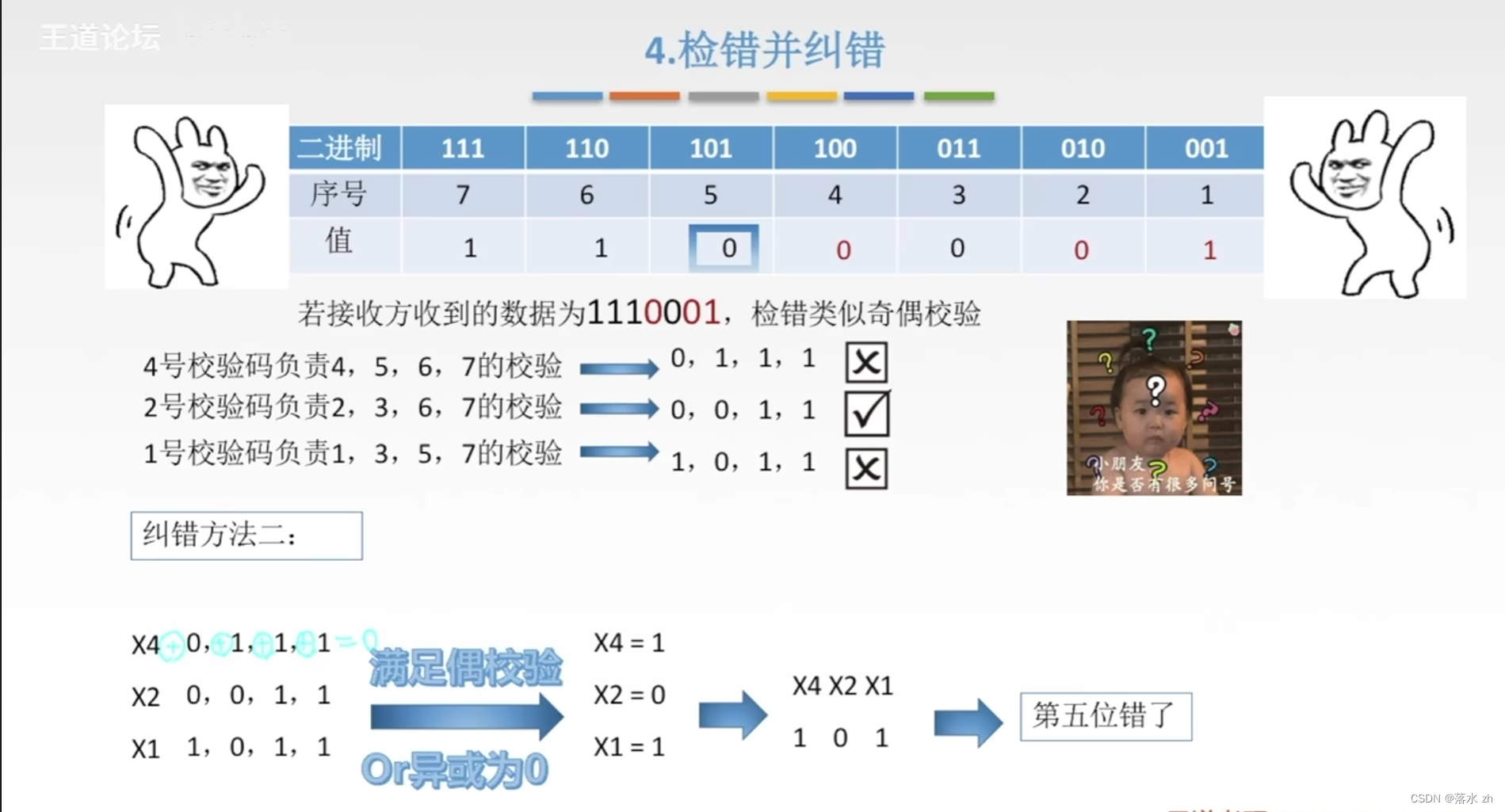
海明码的基本思想是在原始数据位的基础上增加若干校验位(也称作冗余位),形成一个新的编码字。这些校验位被巧妙地分布在编码字的不同位置上,每个校验位负责监督一组特定的数据位,通过计算这些数据位的异或(XOR)值来确定校验位的值。
当数据在传输或存储过程中发生错误时,海明码能够通过比较接收到的编码字中各个校验位与其负责监督的数据位之间的关系,准确地定位出发生错误的比特位置,并在某些情况下直接修正单比特错误。
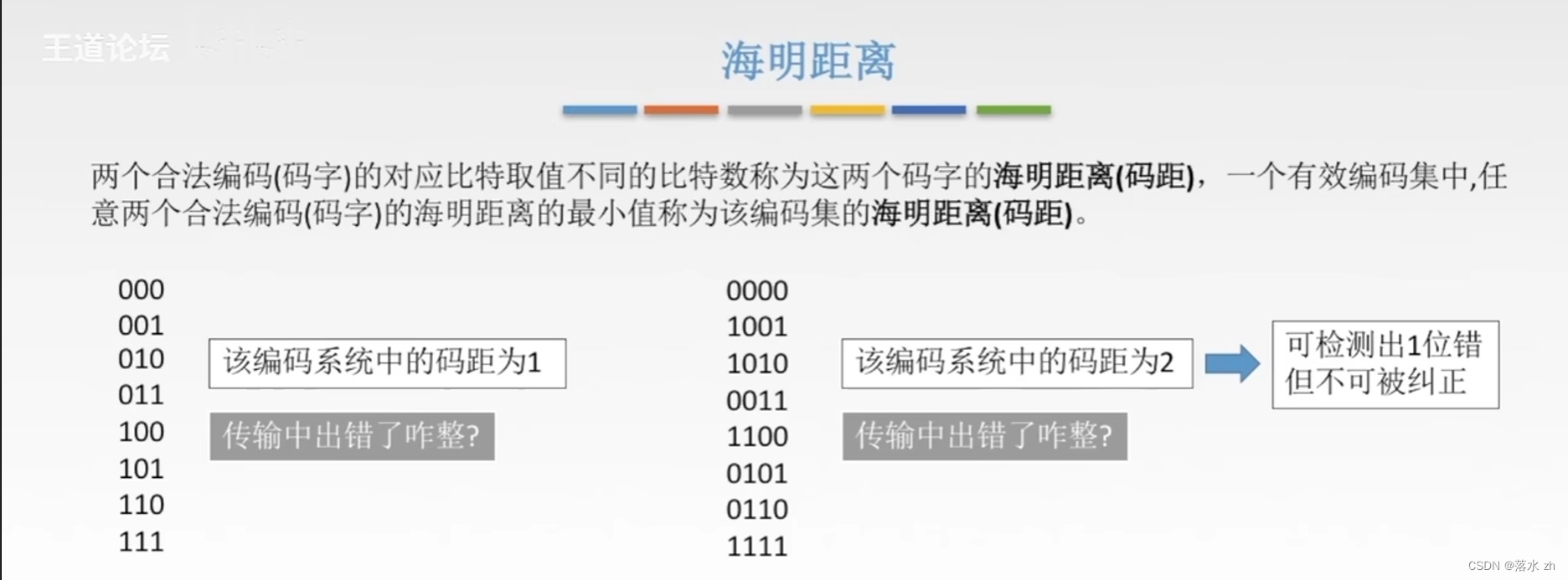
海明距离
海明距离(Hamming Distance)是指两个等长字符串之间对应位置上不同字符的个数。在信息论和编码理论中,尤其是在讨论纠错编码时,这个概念非常关键。它以其发明者理查德·哈明的名字命名。
具体来说,如果我们有两个二进制序列
A=a1a2…an和 B = b1b2…bn ,它们长度都是 ( n ),那么这两个序列的海明距离 ( H(A, B) ) 就是:
( ˝ A , B ) = ∑ i = 1 n ∣ a i − b i ∣ \H(A, B) = \sum_{i=1}^{n} |a_i - b_i|\ (˝A,B)=i=1∑n∣ai−bi∣
由于这里考虑的是二进制数,所以只有两种可能的结果:要么是 0,要么是 1(如果它们不同)。因此,海明距离实际上就是两个序列不相同的比特位的数量。
在纠错编码中,比如海明码,设计的目的是确保任何两个合法编码(即没有错误的编码)之间的海明距离至少达到某个最小值,这样就能保证即使有单个比特错误发生,也能通过比较接收码与预期码之间的海明距离来发现并纠正该错误。
纠错流程
确定校验码的位数r
海明不等式给出了构造纠错码时数据位数(n)、校验位数®以及可纠正错误位数(t)之间的关系。海明不等式表达为:
2 k ≥ ( n + 1 ) 2^{k} \geq(n+1) 2k≥(n+1)
其中,kk 是信息位数(等于原始数据位数),nn 是编码后的码字长度(包括信息位和校验位)
或者:
2 k ≥ m + k + 1 {2^k} \ge {m + k+1} 2k≥m+k+1