问题预览/关键词
- 本节内容是?
- J对w求导的含义是?
- 如何确定切线的方向?
- w在函数J递增处的切线方向是?
- 导数项为正数,w和函数J的关系是?
- w在函数J递减处的切线方向是?
- 导数项为负数,w和函数J的关系是?
笔记
1.本节内容
导数项在做什么?为什么学习率和导数项相乘,会导致w更新?
2.J对w求导
导数项表示函数J在参数w处做一条切线,计算切线的斜率。
- 具体求导公式:课节4.5会详细说明。

3.切线方向
函数J对w某一点的切线方向,与这个点附近函数J的趋势方向一致。
4.w在函数J递增处的切线方向
切线的方向是右上方,切线的斜率为正,代表导数项为正数。
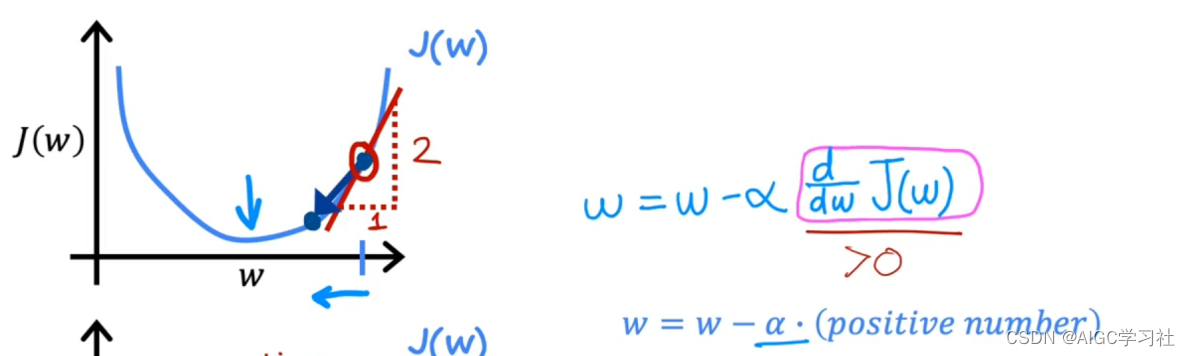
5.导数项为正数
学习率总是正数,导数为正数时,学习率和导数的乘积为正数,因此w不断减去一个正数,w变小也就是向左移动,对应的成本函数J值趋近最小。
6.w在函数J递减处的切线方向
w在函数J递减处的切线:切线的方向是右下方,切线的斜率为负,代表导数项为负数。
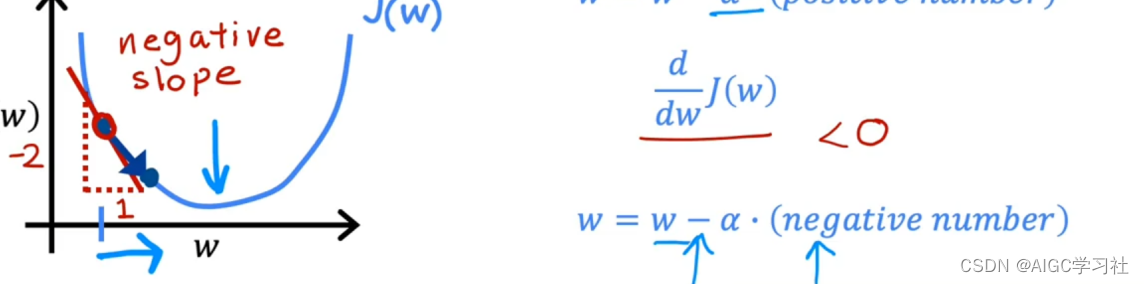
7.导数项为负数
学习率总是正数,导数为负数时,学习率和导数的乘积为负数,因此w不断减去一个负数,w变大也就是向右移动,对应的成本函数J值趋近最小。
总结
本节课没有详细说明导数项是如何计算的,主要强调的是为什么导数项可以通过更新w的方式,来最小化成本函数。观察w和J(w)的二维图,导数项实际是函数J对w切线的斜率。切线的方向是根据w对应的函数J趋势的方向绘制的。学习率总是一个正数,如果切线是右上方,代表斜率为正,导数项为正数,导数项和学习率乘积为正,因此更新w会让w不断减小,对应的成本函数值也会趋近最小化。如果切线是右下方,代表斜率为负,导数项为负数,导数项和学习率乘积为负,因此更新w会让w不断增加,也会最小化成本函数。