编者按： 对于大语言模型的微调训练来说，传统的全参数微调方法需要处理数百万甚至数十亿级别的参数，计算量和显存占用都非常大。而 LoRA 这种技术方案，通过引入少量的可训练矩阵来调整预训练模型的行为，极大降低了训练所需的计算资源，是近年来大语言模型微调的一个重大突破。

我们今天为大家带来的文章，介绍了众多具有代表性的 LoRA 改进方法：LoRA+ 通过为两个矩阵引入不同的学习率提高训练效率；VeRA 和 LoRA-FA 通过训练更少的参数降低计算量；LoRA-drop 和 AdaLoRA 通过动态选择需要训练的层提高效率；DoRA通过将权重分解为权重方向和权重绝对值这两个独立的部分提高模型性能；Delta-LoRA则引入额外的梯度训练预训练矩阵，在几乎不增加计算开销的情况下引入更多可训练参数。

当然，这些技术只是其中的一部分，远不能算是一篇完整的综述。我们希望今天分享的这篇文章能够给大家带来新的启发。

作者 | Dorian Drost

编译 | 岳扬

🚢🚢🚢欢迎小伙伴们加入AI技术软件及技术交流群，追踪前沿热点，共探技术难题~

LoRA 形形色色，种类繁多。图片由 Lucas George Wendt 在 Unsplash 上提供。

低秩自适应（Low-Rank Adaptation，LoRA）可以被视为在针对特定任务高效训练大语言模型方面的重大突破。近年来，这项技术在诸多应用领域获得了广泛认可，并促进了学术界对如何优化其核心技术路线的持续探索，以期进一步提升模型性能或加快模型训练速度。

在本文中，我打算概要介绍一些 LoRA 的不同形式，它们有望以不同的方式增强 LoRA 的能力。我将首先介绍原始 LoRA 技术的基本概念，然后介绍 LoRA+、VeRA、LoRA-FA、LoRA-drop、AdaLoRA、DoRA 和 Delta-LoRA。我将介绍每种方法的基本概念和主要思想，并展示这些方法与原始 LoRA 技术的不同之处。除非对于讲解某项技术的基本概念来说比较重要，否则我会避免涉及技术细节，并且也不会详细讨论这些技术的相关评估问题。对此感兴趣的读者，可通过阅读文末提供的参考文献深入了解。

01 LoRA

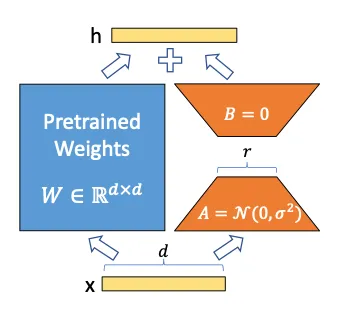
LoRA 的主要思想是在预训练的权重矩阵 W 旁边添加两个较小的可调整矩阵 A 和 B，而不更改 W 的参数。图片来自 [1]。

低秩自适应（Low-Rank Adaptation，LoRA）[1]是目前广泛用于大语言模型（LLMs）训练的一种技术。大语言模型具备根据自然语言输入预测后续 tokens 的能力。这是一种令人惊讶的能力，但对于解决许多实际问题来说，这还远远不够。在大多数情况下，我们需要根据特定的下游任务对大语言模型（LLM）进行微调训练，例如对句子进行分类或为给定问题生成答案。最直接的做法是微调（fine-tuning），即使用所需任务的数据来训练语言模型的某些层。然而，这意味着在微调过程中，需要处理数百万到数十亿的参数量。

但 LoRA 提供了一种能够使参数数量大幅减少的替代方法，因此训练起来更快、更容易。除了已经预训练过的语言模型层的参数权重之外，LoRA 还引入了两个被称为 adapters 的矩阵 A 和 B，这些矩阵要小得多。如果原始参数矩阵 W 的大小为 d x d，则矩阵 A 和 B 的大小分别为 d x r 和 r x d，其中 r 要小得多（通常低于 100）。参数 r 称为秩。也就是说，如果使用秩为 r=16 的 LoRA，则这些矩阵的大小为 16 x d。这种方法可能可以提升模型性能，但另一方面会需要更多的计算时间。

现在有了新矩阵 A 和 B，它们会发挥什么作用呢？输入给 W 的内容同时也会输入给 BA，而 BA 的输出则会添加到原始矩阵 W 的输出中。换句话说，您会在原有的预训练模型基础上，额外进行一些操作，并将它们的输出添加到 original prediction （译者注：指的是在没有添加额外参数的情况下，使用原始预训练模型（即仅使用权重矩阵 W）得到的预测结果。）中，从而影响模型的行为。不再对 W 进行训练，这就是为什么有时我们会说 W 被冻结了。 重要的是，将矩阵 A 和矩阵 B 的输出添加到原始预训练模型输出的这个过程不仅仅在最后一步进行（这样只会在原有模型结构的顶部添加一个新的层），而且可以应用到神经网络深处的层中。

这就是 LoRA 的主要理念，它的最大优势在于，与全参数微调相比，需要训练的参数更少，但仍能获得相当的性能。 这里我还想提一个技术细节：最初，矩阵 A 被初始化为均值为 0 但具有适当方差的随机值，而矩阵 B 则被初始化为全 0 矩阵。这样可以确保 LoRA 矩阵不会从一开始就以随机方式改变原始 W 的输出。一旦 A 和 B 的参数朝着所需的方向调整，它们对 W 的输出的更新应该是对原始输出的一种增量。不过，我们稍后会看到，有些方法由于不同的原因偏离了这一思路。

前文介绍的 LoRA 技术目前已在大语言模型中广泛应用。然而，为了提升训练效率、模型性能或两者兼顾，研究人员提出了多种 LoRA 的变体，通过不同方式对原始LoRA方法进行改进。接下来，我将向大家概述其中一些经过修改的 LoRA 技术。

02 LoRA+

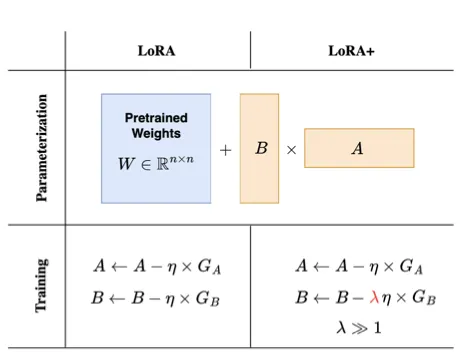
LoRA+ 为两个矩阵 A 和 B 引入了不同的学习率（learning rates），这里用参数 λ 表示。 图片来自 [2]。

LoRA+ [2] 为矩阵 A 和矩阵 B 引入了不同的学习率，从而引入了一种更有效的 LoRA adapters 训练方法。大多数情况下，在训练神经网络时，所有权重矩阵都采用相同的学习率。然而，对于 LoRA 中使用的 adapters 矩阵，LoRA+ 的作者可以证明，单一学习率并不是最优的。将矩阵 B 的学习率设置得比矩阵 A 的学习率高得多，训练就能变得更加高效。

这种方法有其理论依据，主要是为了应对层数非常多的神经网络或宽度较大的神经网络在初始化过程中可能遇到的数值不稳定性或梯度消失等数值计算问题。然而，证明这一点所需的数学计算相当复杂（如果你真的对此感兴趣，可以查看原论文 [2]）。直觉上，你可能会认为，初始化为零的矩阵 B 可以使用比随机初始化的矩阵 A 更大的更新步长（update steps）。此外，也有经验证明这种方法确实能带来较大地改进。通过将矩阵 B 的学习率（learning rate）设定为矩阵 A 的 16 倍，能够小幅提高模型的准确率（约 2%），同时将 RoBERTa 或 Llama-7b 等模型的训练速度加快 2 倍。

03 VeRA

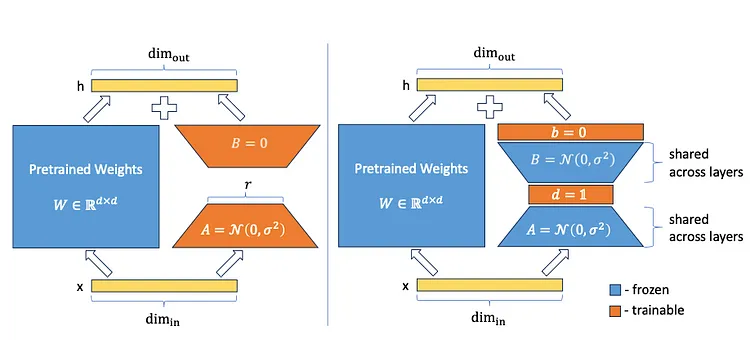
VeRA 不训练矩阵 A 和 B，而是将输入数据映射到一个较低维度的空间（random projection），并训练额外的向量 d 和 b。图片来自 [3]。

通过使用 VeRA（Vector-based Random Matrix Adaptation）[3]，引入了一种能够明显减少 LoRA adapters 参数数量的方法。与 LoRA 直接训练矩阵 A 和 B 不同（这也是 LoRA 的核心理念），LoRA+ 将这些矩阵初始化为共享的随机权重（即所有层中的矩阵 A 和 B 具有相同的权重值），并引入了两个新的可训练向量 d 和 b 。在训练过程，LoRA+ 仅优化向量 d 和 b 的参数值。

你可能会问，这怎么可能行得通呢？A 和 B 是随机权重矩阵。如果不对它们进行训练，它们怎么会对模型的性能有任何贡献呢？这种方法基于一种有趣的技术，即所谓的 random projections（译者注：一种较为常用的数据降维方法）。有诸多研究表明，在大型神经网络中，只有一小部分权重对引导模型行为和达到所需任务性能起关键作用。由于采用了随机初始化，从一开始模型的某些子网络对所需行为的贡献就更大一些。在训练过程中，虽然会优化所有参数，但现在无从得知哪些子网络更为重要。这导致训练开销非常大，因为绝大部分参数的更新对模型预测能力的提升并无实质性贡献。

基于这一思路，一些方法试图只训练这些相关的子网络。与直接训练子网络不同，它们在矩阵之后引入了projection vectors（译者注：用于将神经网络中的某些权重或特征从一个空间投影到另一个空间的向量），通过将矩阵与这些向量相乘，可以获得等效于在矩阵中调整某些稀疏参数（sparse parameters）。这是 VeRA 作者提出的思路，他们引入了可训练的向量 d 和 b ，同时冻结了矩阵 A 和 B 。另外，与原始 LoRA 技术不同，VeRA 中矩阵 B 的初始化也采用了随机值，而非全零矩阵。通过这种方式，VeRA 期望以更小的计算开销达到类似的效果。

这种方法使得所需参数数量远少于完整的矩阵 A 和 B 。 举个例子，在 GPT-3 中引入秩为 16 的 LoRA 层需要 75.5M 参数，而使用 VeRA 只需 2.8M 参数，参数量减少了 97 %。尽管参数大幅减少，VeRA作者在一些常见的大模型基准测试（如GLUE或E2E）以及基于 RoBERTa 和 GPT2 Medium 的模型上进行了评估，结果表明 VeRA 模型的性能只比全参数微调或原始 LoRA 技术的模型稍差一些。

04 LoRA-FA

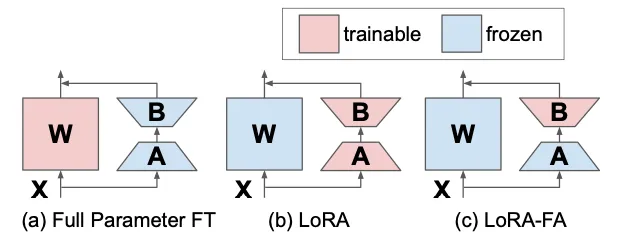
LoRA-FA 冻结矩阵 A，只训练矩阵 B。图片来自 [4]。

另一种方法是 LoRA-FA [4]，即 LoRA with Frozen-A，其思路与方向与 VeRA 类似。在 LoRA-FA 中，矩阵 A 在初始化后被冻结，因此可用作 random projection 。矩阵 B 在初始化为零（就像原始 LoRA 技术一样）后进行训练，而不是添加新向量。这样，参数数量减少了一半，而性能却与使用普通 LoRA 技术相当。

05 LoRa-drop

LoRA-drop 使用 B*A 的输出来决定哪些 LoRA 层值得训练。图片来自 [5]。

文章一开始，我就解释过，我们可以在神经网络的任何一层添加 Lora 矩阵。LoRA-drop [5] 引入了一种算法来决定哪些层值得通过 LoRA 进行增强，哪些层不值得这样做。即使训练 LoRA adapters 比微调整个模型要便宜得多，但添加的 LoRA adapters 越多，训练成本就越高。

LoRA-drop 技术包括两个步骤。第一步，从整个数据集中随机选择一个子集，并对 LoRA adapters 进行多次迭代训练。然后，以 BAx 计算每个 LoRA adapter 的重要性，其中 A 和 B 是 LoRA 矩阵，x 是输入。这只是简单地将 LoRA adapter 的输出与冻结层（frozen layer）的输出相加。如果通过计算得到的输出值较大，则表示冻结层的行为发生了很大变化。如果很小，这意味着 LoRA adapter 对冻结层的影响很小，可以被省略。

基于之前计算得到的结果，选择哪些 LoRA 层对模型的性能影响最大，有多种不同的方法。可以将重要性值相加，直到达到一个由超参数控制的阈值，或者只选择重要性最高的前 n 个LoRA层。不管采用哪种方式，在接下来的训练步骤中，都会在整个数据集上进行全面训练（之前使用的是数据子集），但只会优化那些已选择的 LoRA 层的参数，而其他层的参数将被冻结为一组共享的值，在训练过程中保持不变。

因此，LoRA-drop 算法允许只使用 LoRA 层的子集来训练模型。作者提出的实证证据表明，与训练所有 LoRA 层相比，通过 LoRA-drop 训练的模型的准确率（accuracy）仅有微小变化，但由于需要训练的参数数量减少，计算时间也有所缩短。

06 AdaLoRA

AdaLoRA 允许动态调整 LoRA 矩阵的秩**。照片由 Hasmik Ghazaryan Olson 发布于 Unsplash。

那么如何判断哪些 LoRA 参数比其他参数更重要呢？在本节将介绍 AdaLoRA [6] 这项技术，即Adaptive LoRa。AdaLoRA 中自适应（adaptive）的是 LoRA 矩阵的秩。与前一节的问题类似，可能没有必要将同样大小的 LoRA 矩阵 A 和 B 添加到每一层，因为对于某些更为重要的模型层（那些可能导致模型行为发生较大变化的层），使用 LoRA 进行训练可能效果更好。为了确定哪些模型层更为重要， AdaLoRA 的作者提出考虑 LoRA 矩阵的奇异值（singular values）作为判断模型层重要性的指标。

这是什么意思呢？首先，我们必须明白，矩阵乘法也可以看作是将函数应用于向量。在处理神经网络时，这一点是非常明显的：大多数情况下，神经网络都是作为函数来使用的，即给出一个输入（例如像素值矩阵），然后得到一个结果（例如将图像归类到预定义的类别或标签中的某一类）。在背后，这个函数应用是由一系列的矩阵乘法驱动的。现在，假设你想减少矩阵中的参数数量。这样会改变函数的行为，但你希望它的变化越小越好。一种方法是计算矩阵的特征值（eigenvalues），它可以帮助我们了解矩阵中每一行的方差。然后可以将矩阵中方差很小的行的值设为零，这些被设置为零的行在数据中仅提供很少的信息，对于模型的训练或结果并没有太大的影响，因此可以被视为不重要的部分而被忽略。这就是 AdaLoRA 的主要思想，因为前述的奇异值正是特征值的平方根。也就是说，根据奇异值，AdaLoRA 可以决定哪些 LoRA 矩阵的哪些行更重要，哪些可以省略。这就有效地缩小了一些矩阵的秩，因为这些矩阵有很多行并没有太大的贡献。但是，请注意这种技术与上一节的 LoRA-drop 有一个重要的区别：在 LoRA-drop 中，LoRA 层的 adapters 要么被选择完全训练，要么完全不训练。AdaLoRA 可以决定保留某些层的 adapters  ，但其秩较低。这意味着，最终，不同的 adapters 可以具有不同的秩（而在最初的 LoRA 方法中，所有的adapters 都具有相同的秩） 。

这是对 AdaLoRA 方法的简要概述，但有一些细节我为了简洁起见省略了。不过，我想提及其中的两个细节：首先，AdaLoRA 方法并不总是直接去计算奇异值（因为这样做成本很高），而是使用奇异值分解（singular value decomposition，SVD）来分解权重矩阵。尽管奇异值分解（SVD）技术将原始矩阵分解为多个矩阵，但这些分解后的矩阵组合包含了与原始矩阵相同的信息。与直接计算奇异值相比，使用 SVD 分解的好处在于可以更有效地获取奇异值，而不需要进行更多复杂和昂贵的计算。其次，AdaLoRA 不仅仅根据奇异值来做出决定，还考虑了 loss 值对某些参数的敏感程度。如果将某个参数设置为零对 loss 值会产生很大影响，则该参数被认为具有较高的敏感性。在确定应该降低哪些秩的过程中，不仅关注奇异值较小的行，同时也要分析这些行元素对模型预测结果的敏感程度。

通过将 AdaLoRA 与相同 rank budget （译者注：可用于分配给 adapters 矩阵的资源数量）的原始 LoRA 技术进行比较，可以获得该方法的 empirical evidence （译者注：基于观察、实验或实际经验所得到的证据或数据）。也就是说，两种方法在总参数数量上是相同的，但参数分配方式不同而已。在 LoRA 中，所有矩阵都具有相同的秩，而在 AdaLoRA 中，有一些重要层的矩阵秩较高，另一些不太重要的模型层的矩阵秩较低。尽管如此，最终 LoRA 和 AdaLoRA 的参数总数量还是相同的。在许多场景下，AdaLoRA 相比标准 LoRA 方法表现更加出色，这验证了 AdaLoRA 可以更好地将可训练参数分配到对特定任务至关重要的模型部分上。下图举例说明了 AdaLoRA 为给定模型分配秩的方式。正如我们所见，它给了模型末尾的层更高的秩，表明调整这些层对目标任务性能的提升更为重要。

在神经网络的不同层上，LoRA 矩阵被赋予不同的秩。通常来说，较后的层的秩更高。图片来自 [6]。

07 DoRA

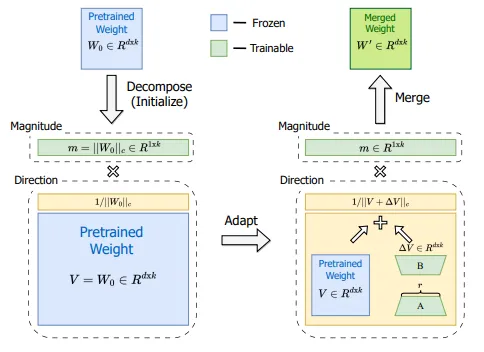
在 DoRA 中，权重矩阵 W 被分解为权重绝对值（magnitude） m 和权重方向（direction） V，它们可以独立调整。图片来自 [7]。

对 LoRA 进行修改以获得更好性能的另一种方法是权重分解的低秩自适应（Weight-Decomposed Low-Rank Adaption），或称为 DoRA [7]。DoRA 的出发点是，每个矩阵都可以分解为权重绝对值和权重方向的乘积。 对于二维空间中的向量，可以很容易地将其可视化出来：一个向量不过就是一个从零点开始、指向向量空间某个点的箭头。通过向量的各个分量的数值，可以唯一确定空间中的一个点的位置，比如说如果某个空间有两个维度 x 和 y，可以通过 x=1 和 y=1 来表示。或者，可以用长度和角度（即方向）来描述同一个点，比如 m=√2 和 a=45°。也就是说，从零点开始，沿着 45°的方向移动，移动距离为 √2，最终到达相同的点（x=1，y=1）。

将矩阵分解为长度和方向的方法同样适用于高阶矩阵。DoRA 的作者将其应用于权重矩阵，研究了使用普通微调方法训练的模型和使用 LoRA adapters 训练的模型在训练步骤中的权重矩阵更新情况。这两种技术的比较见下图：

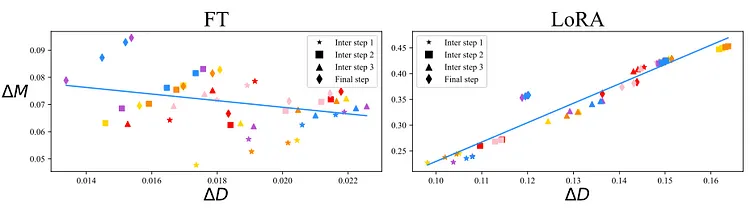
普通微调和 LoRA 的不同之处在于权重绝对值和权重方向变化之间的关系。图片来自 [7]。

可以看到两幅图表，一幅是通过普通方法微调的模型（左侧），另一幅是使用 LoRA adapters 训练的模型（右侧）。在 x 轴上，我们可以看到权重方向的变化，而在 y 轴上，我们看到权重绝对值的变化，图表中的每个散点都属于模型的一层。这两种训练方法有一个重要区别。在左图中，权重方向更新和权重绝对值更新之间只存在微弱的负相关性，而在右图中，存在一种更强的正相关性。哪种更好？或者有无任何意义？请记住，LoRA 的主要理念是用更少的参数实现与普通微调相同的性能。这意味着，在不增加成本的前提下，我们希望 LoRA 的训练与普通微调方法有尽可能多的相同特性。 如果微调中权重方向和权重绝对值之间的相关性稍微为负，那么这也可能是 LoRA 所希望拥有的特性。换句话说，如果 LoRA 中权重方向和权重绝对值之间的关系与全参数微调相比不同，那么这可能是 LoRA 有时表现不及普通微调方法的原因之一。

DoRA 的作者介绍了一种方法，通过将预训练矩阵 W 分解为大小为 1 x d 的权重绝对值向量 m 和权重方向矩阵 V，来独立训练权重绝对值和权重方向。然后通过 B*A 来增强权重方向矩阵 V，而 m 则保持不变，这种方法是可行的，因为 m 只有一个维度。虽然 LoRA 倾向于同时改变权重绝对值和方向（这两者之间的正相关性较高就表明了这一点），但 DoRA 更容易调整其中一个而不影响另外一个，或者通过负改变来补偿另一个的改变。我们可以看到权重方向和权重绝对值之间的关系更像是普通微调方法中的关系：

对于 DoRA，权重绝对值和方向之间的关系更类似于普通微调方法中的关系。图片来自 [7]。

在多个基准测试中，DoRA 的准确率都优于 LoRA。将权重矩阵的更新分解为 magnitude 和 direction 可能使 DoRA 这种训练方法更接近微调，同时还能使用 LoRA 引入的更小的参数空间。

08 Delta-LoRA

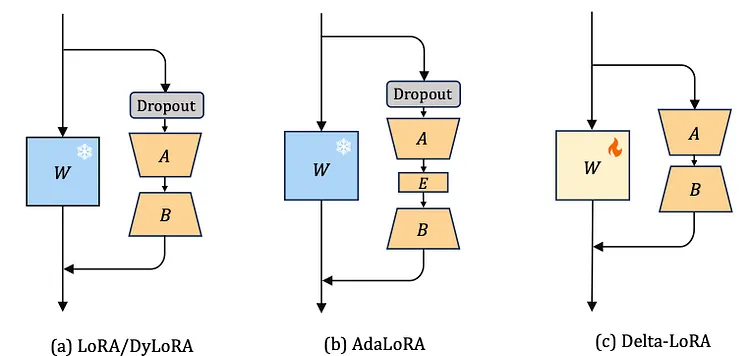
Delta-LoRA 不会冻结矩阵 W，而是根据从 B*A 中获得的梯度进行更新。图片来自 [8]。

Delta-LoRA [8] 引入了另一种改进 LoRA 的思路。这一次，预训练矩阵 W 将再次发挥作用。请记住，LoRA 的主要思想是不要（！）调整预训练矩阵 W，因为这样做消耗的成本太高（属于普通的微调方法）。这也是 LoRA 引入较小矩阵 A 和 B 的原因。然而，这些较小矩阵学习下游任务的能力较弱，这也就是为什么使用 LoRA 技术训练的模型，其性能通常低于使用普通微调方法训练的模型的原因。在训练过程中对 W 进行调整固然很好，但需要耗费的资源确实太多了。

Delta-LoRA 的作者建议通过使用 AB 的梯度（即 AB 在两个连续 time steps 中的差值）来更新矩阵 W。 这个梯度会乘以一些超参数 λ 进行缩放，以控制新的训练方法对预训练权重的影响程度，然后加到 W 上（其中 α 和 r（秩）是原始 LoRA 配置中的超参数）：

W 是根据连续两个 time steps 中 A*B 之间的差值进行更新。图片来源于[8]。

这就在几乎没有计算开销的情况下，引入了更多需要训练的参数。 我们不必像普通微调方法那样计算整个矩阵 W 的梯度，而是使用在 LoRA 训练中已经得到的梯度来更新它。作者使用 RoBERTA 和 GPT-2 等模型在多个基准测试上评估了这种方法，发现与原始 LoRA 方法相比，这种方法的性能有所提升。

09 Summary

恭喜！你已经快阅读完本文了，终点就在眼前！照片由 Unsplash 的 David Griffiths 提供。

前文介绍了多种不同的方法，它们都期望改变 LoRA 的核心思想，进一步减少计算时间或提高性能（或两者兼有之）。最后，我将对这些方法进行简要总结：

• LoRA 引入了经过训练的低秩矩阵 A 和 B，同时冻结了预训练的权重矩阵 W。
• LoRA+ 建议为 B 设置比 A 更高的学习率。
• VeRA 不训练低秩矩阵 A 和 B，而是随机初始化它们，并在其上训练新的向量 d 和 b。
• LoRA-FA 只训练低秩矩阵 B。
• LoRA-drop 使用 B*A 的输出来确定哪些模型层值得进行训练。
• AdaLoRA 动态调整不同层中 A 和 B 的秩，允许在一些重要的模型层中使用更高的秩，这些层对模型性能的贡献更大。
• DoRA 将 LoRA adapter 分为 magnitude 和 direction 两个部分，使它们的训练更加独立。
• Delta-LoRA 通过 A*B 的梯度来改变 W 的权重。

LoRA 及其相关方法的研究非常丰富、异常活跃，几乎每天都有新的研究成果涌现。我想通过本文介绍一些 LoRA 方法的核心思想。当然，本文介绍的这些 LoRA 技术只是其中的一小部分，远不能算是一篇完整的综述。

LoRA 及其相关方法的研究潜力巨大，我们希望这篇文章能够给大家带来新的启发。我想，在提高大语言模型的训练性能或进一步减少计算时间这些领域，很快就会有新的突破性进展出现。

10 参考文献和可供深入学习的文献资料

下列是本文所介绍技术的相关论文：

[1] LoRA: Hu, E. J., Shen, Y., Wallis, P., Allen-Zhu, Z., Li, Y., Wang, S., … & Chen, W. (2021). Lora: Low-rank adaptation of large language models. arXiv preprint arXiv:2106.09685.

[2] LoRA+: Hayou, S., Ghosh, N., & Yu, B. (2024). LoRA+: Efficient Low Rank Adaptation of Large Models. arXiv preprint arXiv:2402.12354.

[3] VeRA: Kopiczko, D. J., Blankevoort, T., & Asano, Y. M. (2023). Vera: Vector-based random matrix adaptation. arXiv preprint arXiv:2310.11454.

[4]: LoRA-FA: Zhang, L., Zhang, L., Shi, S., Chu, X., & Li, B. (2023). Lora-fa: Memory-efficient low-rank adaptation for large language models fine-tuning. arXiv preprint arXiv:2308.03303.

[5] LoRA-drop: Zhou, H., Lu, X., Xu, W., Zhu, C., & Zhao, T. (2024). LoRA-drop: Efficient LoRA Parameter Pruning based on Output Evaluation. arXiv preprint arXiv:2402.07721.

[6] AdaLoRA: Zhang, Q., Chen, M., Bukharin, A., He, P., Cheng, Y., Chen, W., & Zhao, T. (2023). Adaptive budget allocation for parameter-efficient fine-tuning. arXiv preprint arXiv:2303.10512.

[7] DoRA: Liu, S. Y., Wang, C. Y., Yin, H., Molchanov, P., Wang, Y. C. F., Cheng, K. T., & Chen, M. H. (2024). DoRA: Weight-Decomposed Low-Rank Adaptation. arXiv preprint arXiv:2402.09353.

[8]: Delta-LoRA: Zi, B., Qi, X., Wang, L., Wang, J., Wong, K. F., & Zhang, L. (2023). Delta-lora: Fine-tuning high-rank parameters with the delta of low-rank matrices. arXiv preprint arXiv:2309.02411.

如果想进一步了解 random projection 相关技术，可以阅读下列文献：

Frankle, J., & Carbin, M. (2018). The lottery ticket hypothesis: Finding sparse, trainable neural networks. arXiv preprint arXiv:1803.03635.

想获得对 LoRA 和 DoRA 更详细的了解，我推荐阅读这篇文章：

https://magazine.sebastianraschka.com/p/lora-and-dora-from-scratch

Thanks for reading!

END

本文经原作者授权，由 Baihai IDP 编译。如需转载译文，请联系获取授权。

原文链接：

https://towardsdatascience.com/an-overview-of-the-lora-family-515d81134725