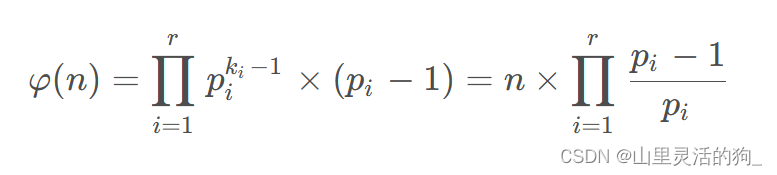蓝桥杯练习笔记（十五）

一、

首先要会欧拉函数去找到对应数字的所有互质的数的个数，然后要会快速幂去计算这种指数超级大的数字的幂积结果。
先学会第一个：欧拉函数。这个博主讲得不错，很清晰易懂。能够理解以下的公式来源和意义就行

再一个就是要会快速幂运算：快速幂。
其本质是根据数字的唯一分解定理来将指数转化为二进制，从而这个乘积被分为多个底数的特定次方之间的乘积，然后一直对底数不断地平方来快速达到这几个特定次方从而实现快速的幂运算。

• 以下是蓝桥官网的一个题解：

//本题主要考察欧拉函数和快速幂
//欧拉函数Euler(n):表示不大于n且与n互质的正整数的个数,Euler(1)=1
//由唯一分解定理,n=p1^k1*p2^k2*...*pn^km,pi均为质数,ki是其幂次
//由此可推出欧拉函数的求法:Euler(n)=n/p1*(p1-1)/p2*(p2-1)/.../pn*(pn-1)
//将欧拉函数的模板背下来即可
//由欧拉函数的模板可知,若已知Euler(a)=m,则Euler(a^b)=m*(a^(b-1))
//故先求Euler(a),再用快速幂求a^(b-1),二者相乘即为最终答案 
#include <bits/stdc++.h>using namespace std;const int mod=998244353;typedef unsigned long long ull;ull quick_power(ull base,ull power,ull mod)//快速幂算法 
{ull res=1;while(power){if(power&1)res=res*base%mod;base=base*base%mod;power=power>>1;    }    return res%mod;
}ull Euler(ull n)//求n的欧拉函数(固定模板) 
{ull phi=n;for(int i=2;i*i<=n;i++)//枚举n的质因数 {if(n%i)continue;while(n%i==0)//i是质因数 {n=n/i;//n不断除以i直至i不再是n的质因数 }phi=phi/i*(i-1);//递推欧拉函数,Euler(n)=n/pi*(pi-1) }    //最后可能还剩下一个大于n的因子,如12=2*2*3,最后将剩下3,补充上 if(n>1)phi=phi/n*(n-1);return phi;
}
//由如上算法可知,n的欧拉函数只与其质因数的组成有关,与每个质因数的个数无关
//对于不同的数字,只要它们的质因数组成相同,计算过程中就会除以相同的pi乘以相同的(pi-1)
//故若m和n的质因数组成相同,m是n的k倍,则Euler(m)也是Euler(n)的k倍
//而a^b是a的a^(b-1)倍,则由此推出Euler(a^b)=Euler(a)*(a^(b-1)),此即为最终答案int main()
{ull a,b;cin>>a>>b;ull Euler_a=Euler(a);//对a求欧拉函数//最终答案:Euler(a)*a^(b-1) ull ans=Euler_a*quick_power(a,b-1,mod)%mod;cout<<ans<<endl;return 0;
}