机器学习-十大算法之一线性回归算法案例讲解
- 一·摘要
- 二·个人简介
- 三·什么是线性回归
- 四·LinearRegression使用方法
- 五·糖尿病数据线性回归预测
- 1.数据说明
- 2.导包
- 3.导入数据
- 4.脱敏处理
- 5.抽取训练数据和预测数据
- 6.创建模型
- 7.预测
- 8.线性回归评估指标
- 9.研究每个特征和标记结果之间的关系.来分析哪些特征对结果影响较大
- 10.结果
- 六·波士顿房价预测
- 1.前言
- 2.数据说明
- 3.数据导入
- 4.查看数据
- 5.查看缺失值
- 6.描述性数据分析
- 7.预测性数据分析
- 8.预测
一·摘要
线性回归是一种用于预测数值型数据的统计学分析方法,它通过建立一个或多个自变量与因变量之间的线性关系来进行预测。
线性回归的基本思想是通过拟合最佳直线(也就是线性方程),来描述自变量和因变量之间的关系。这条直线被称为回归线,其目的是使得所有数据点到这条直线的垂直距离(即残差)的平方和最小。这个最小化过程通常称为最小二乘法。
二·个人简介
🏘️🏘️个人主页:以山河作礼。
🎖️🎖️:Python领域新星创作者,CSDN实力新星认证,CSDN内容合伙人,阿里云社区专家博主,新星计划导师,在职数据分析师。
💕💕悲索之人烈焰加身,堕落者不可饶恕。永恒燃烧的羽翼,带我脱离凡间的沉沦。

| 类型 | 专栏 |
|---|---|
| Python基础 | Python基础入门—详解版 |
| Python进阶 | Python基础入门—模块版 |
| Python高级 | Python网络爬虫从入门到精通🔥🔥🔥 |
| Web全栈开发 | Django基础入门 |
| Web全栈开发 | HTML与CSS基础入门 |
| Web全栈开发 | JavaScript基础入门 |
| Python数据分析 | Python数据分析项目🔥🔥 |
| 机器学习 | 机器学习算法🔥🔥 |
| 人工智能 | 人工智能 |
三·什么是线性回归
线性回归是一种非常简单易用且应用广泛的算法,其原理也非常容易理解,因此非常适合作为机器学习的入门算法。当我们在中学学习二元一次方程时,我们通常将y视为因变量,x视为自变量,从而得到方程:
y = a x + b y = ax + b y=ax+b
其中, a a a 是斜率,表示自变量 x x x 对因变量 y y y 的影响程度; b b b 是截距,表示当 x = 0 x=0 x=0 时 y y y 的值。线性回归的目标就是找到最佳的参数 a a a 和 b b b,使得预测值 y ^ \hat{y} y^ 与实际值 y y y 之间的差异(通常是平方差)最小。
当我们只用一个x来预测y,就是一元线性回归,也就是在找一个直线来拟合数据。比如,我有一组数据画出来的散点图,横坐标代表广告投入金额,纵坐标代表销售量,线性回归就是要找一条直线,并且让这条直线尽可能地拟合图中的数据点。
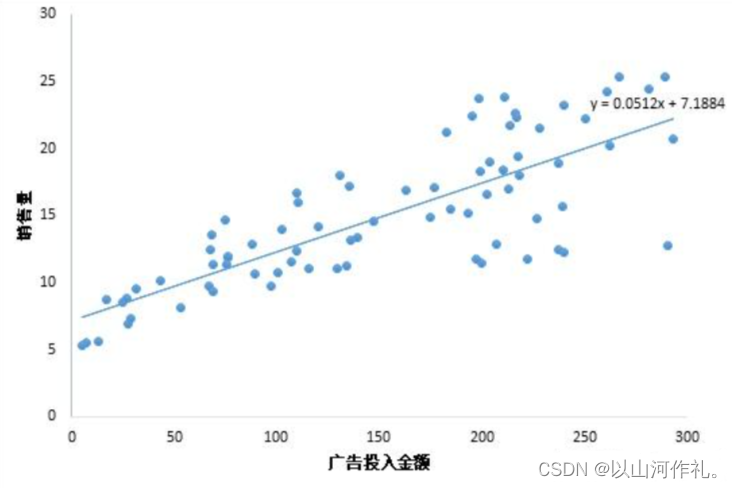
这里我们得到的拟合方程是y = 0.0512x + 7.1884,此时当我们获得一个新的广告投入金额后,我们就可以用这个方程预测出大概的销售量。
线性回归模型可以通过最小化损失函数来求解参数,常用的损失函数是均方误差(Mean Squared Error, MSE)。通过解析方法或数值优化方法,如梯度下降(Gradient Descent),可以找到最优的参数 a a a 和 b b b。
线性回归模型不仅可以用于简单的一元线性回归问题,还可以推广到多元线性回归,即有多个自变量的情况。在多元线性回归中,方程可以表示为:
y = X β + ϵ \mathbf{y} = \mathbf{X}\beta + \epsilon y=Xβ+ϵ
其中, m a t h b f y mathbf{y} mathbfy 是因变量向量, m a t h b f X mathbf{X} mathbfX 是包含所有自变量的矩阵, β \beta β 是参数向量, ϵ \epsilon ϵ 是误差项。
四·LinearRegression使用方法
- 导入库和数据:首先需要导入scikit-learn库,并加载需要进行线性回归分析的数据集。
- 创建模型对象:通过
sklearn.linear_model.LinearRegression()创建一个线性回归模型的对象。在这一步中,您可以根据需要设置模型的参数,例如是否计算截距(fit_intercept)等。 - 训练模型:使用
fit()方法来训练模型。这通常涉及到将训练数据(特征和标签)传递给fit()方法。例如,lineModel.fit(X_train, Y_train),其中X_train是训练特征数据,Y_train是对应的标签数据。 - 进行预测:训练完成后,可以使用
predict()方法来对新的数据进行预测。例如,lineModel.predict(X_test),其中X_test是您想要预测的新数据。 - 评估模型:最后,可以使用
score()方法来评价模型的性能,这通常会给出一个表示模型拟合优度的 R 2 R^2 R2分数或其他指标。
五·糖尿病数据线性回归预测
1.数据说明
diabetes 是一个关于糖尿病的数据集, 该数据集包括442个病人的生理数据及一年以后的病情发展情况。
下面对数据集变量说明下,方便大家理解数据集变量代表的意义:
age:年龄sex:性别bmi(body mass index):身体质量指数,是衡量是否肥胖和标准体重的重要指标,理想BMI(18.5~23.9) = 体重(单位Kg) ÷ 身高的平方 (单位m)bp(blood pressure):血压(平均血压)s1,s2,s3,s4,s4,s6:六种血清的化验数据,是血液中各种疾病级数指针的6的属性值。s1——tc,T细胞(一种白细胞)s2——ldl,低密度脂蛋白s3——hdl,高密度脂蛋白s4——tch,促甲状腺激素s5——ltg,拉莫三嗪s6——glu,血糖水平
【注意】:以上的数据是经过特殊处理,
10个数据中的每个都做了均值中心化处理,然后又用标准差乘以个体数量调整了数值范围。验证就会发现任何一列的所有数值平方和为1。
2.导包
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
- 用于导入三个常用的数据处理和可视化库:numpy、pandas和matplotlib。
from sklearn.linear_model import LinearRegression
- 从sklearn库中导入线性回归模型。
3.导入数据
from sklearn.datasets import load_diabetes
- 从sklearn库中导入糖尿病数据集。
diabetes=load_diabetes()
data = diabetes['data']
target = diabetes['target']
feature_names = diabetes['feature_names']
- 加载糖尿病数据集,并将数据集的特征数据、目标数据和特征名称分别赋值给变量data、target和feature_names。
4.脱敏处理
df = pd.DataFrame(data,columns= feature_names)
df
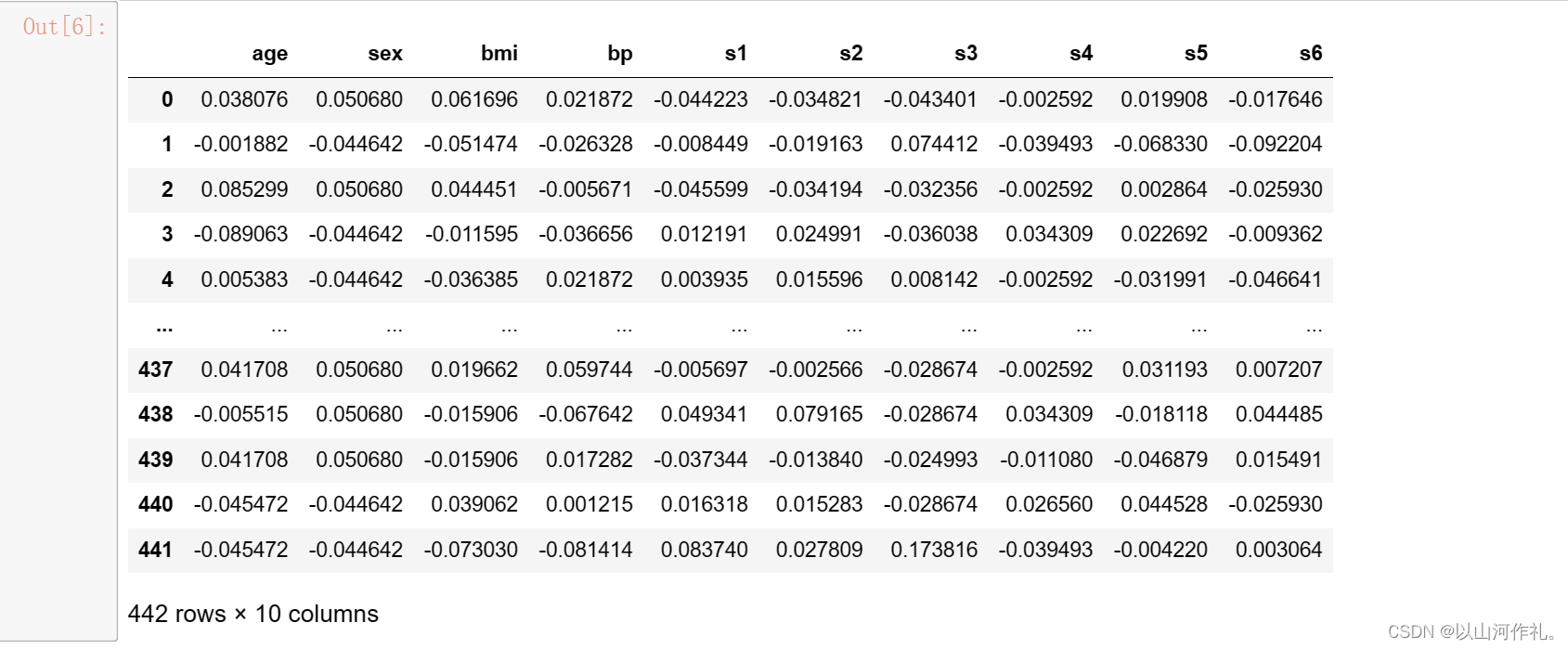
- 使用pandas库创建一个DataFrame对象,并将数据和特征名称作为参数传递给DataFrame构造函数。然后,将创建的DataFrame对象赋值给变量df
5.抽取训练数据和预测数据
from sklearn.model_selection import train_test_split
- 从sklearn库中导入train_test_split函数。train_test_split函数用于将数据集划分为训练集和测试集
x_train,x_test,y_train,y_test = train_test_split(data,target,test_size=0.2)
- 使用train_test_split函数将数据集划分为训练集和测试集。其中,data表示特征数据,target表示目标数据,test_size=0.2表示将20%的数据作为测试集,剩余的80%作为训练集。划分后的训练集和测试集分别赋值给变量x_train、x_test、y_train和y_test。
6.创建模型
liner = LinearRegression()
liner.fit(x_train,y_train)
- 创建一个线性回归模型,并使用训练集数据进行拟合。首先,通过LinearRegression()创建一个线性回归模型对象,然后使用fit()方法将训练集的特征数据x_train和目标数据y_train传入模型进行拟合。
求线性方程: y = WX + b 中的W系数和截距b
df.head(4)

- 显示DataFrame对象df的前4行数据。head()方法默认返回前5行数据,但可以通过传入参数来指定返回的行数
系数w 系数大小类比权重
liner.coef_

- 获取线性回归模型的系数。coef_属性返回一个数组,其中包含模型中每个特征对应的系数值。这些系数表示了每个特征对目标变量的影响程度。
截距b
b= liner.intercept_
b
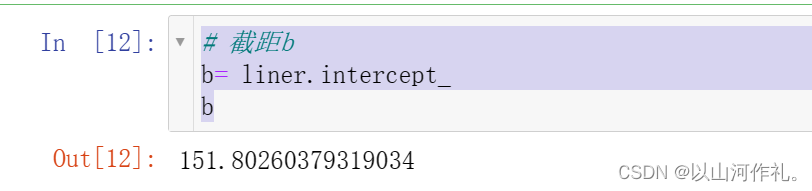
- 获取线性回归模型的截距。intercept_属性返回一个数值,表示模型中的截距值。截距是一个常数项,用于在特征数据为0时预测目标变量的值。
7.预测
y_pred = liner.predict(x_test)
y_pred
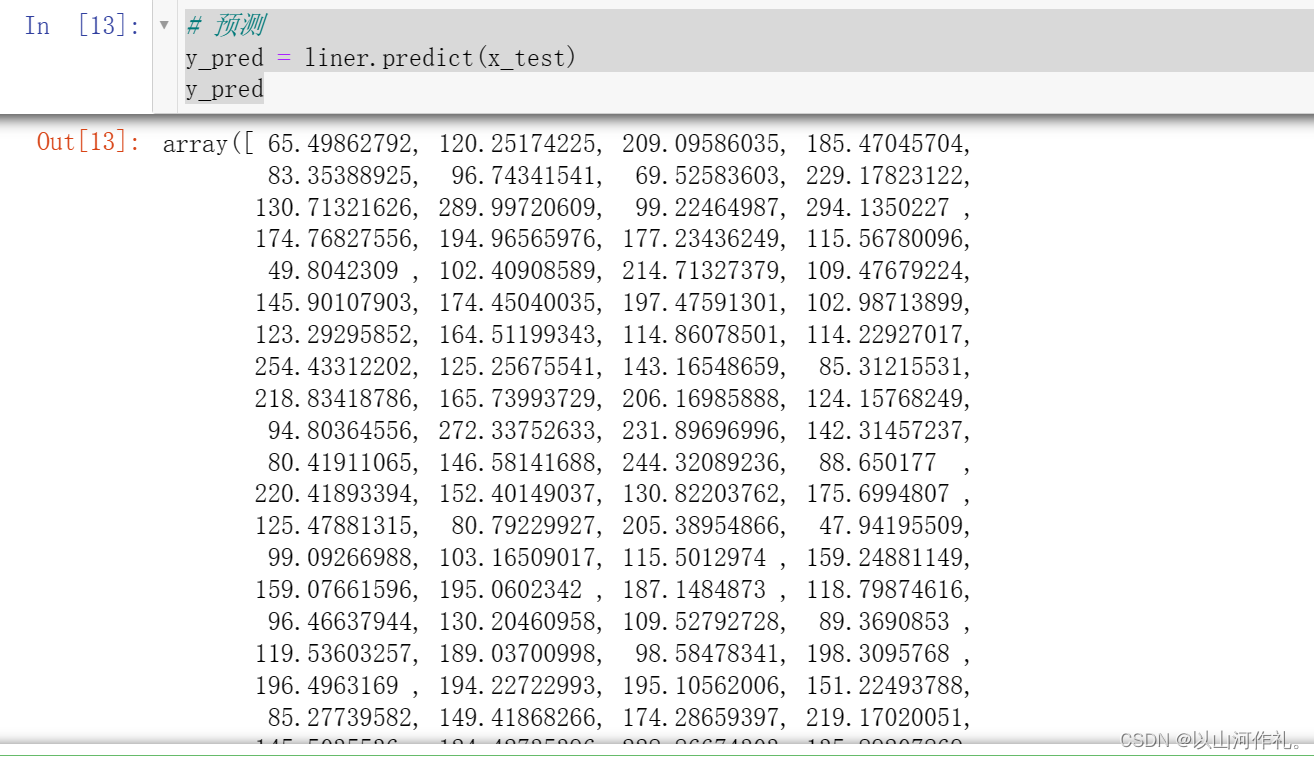
- 使用线性回归模型对测试集数据进行预测,并将预测结果赋值给变量y_pred。predict()方法接受一个特征数据集作为输入,并返回对应的目标变量预测值。
得分,回归的得分一般比较低
liner.score(x_test,y_test)
- 计算线性回归模型在测试集上的拟合优度得分。score()方法接受两个参数,分别是特征数据集和目标变量数据集,返回一个数值表示模型的拟合优度得分。在这里,输入的测试集特征数据为x_test,目标变量数据集为y_test,输出的拟合优度得分为liner.score(x_test, y_test)
8.线性回归评估指标
# metrics 评估from sklearn.metrics import mean_absolute_error as msemse(y_test,y_pred)
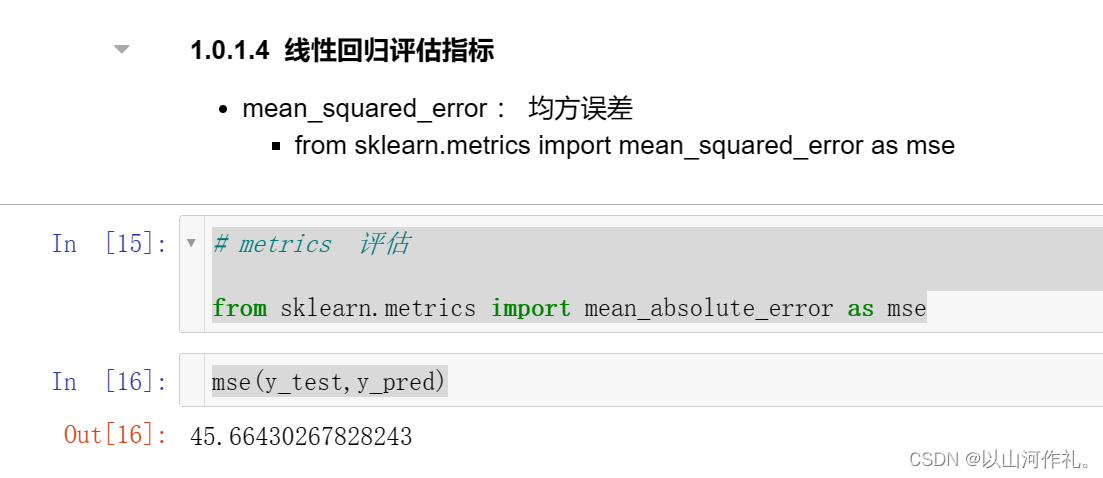
- 计算线性回归模型在测试集上的均方误差(Mean SquaredError,MSE)。mean_absolute_error函数用于计算平均绝对误差,但在这里被重命名为mse。输入的参数为真实目标变量数据集y_test和预测目标变量数据集y_pred,输出的结果为均方误差。
9.研究每个特征和标记结果之间的关系.来分析哪些特征对结果影响较大
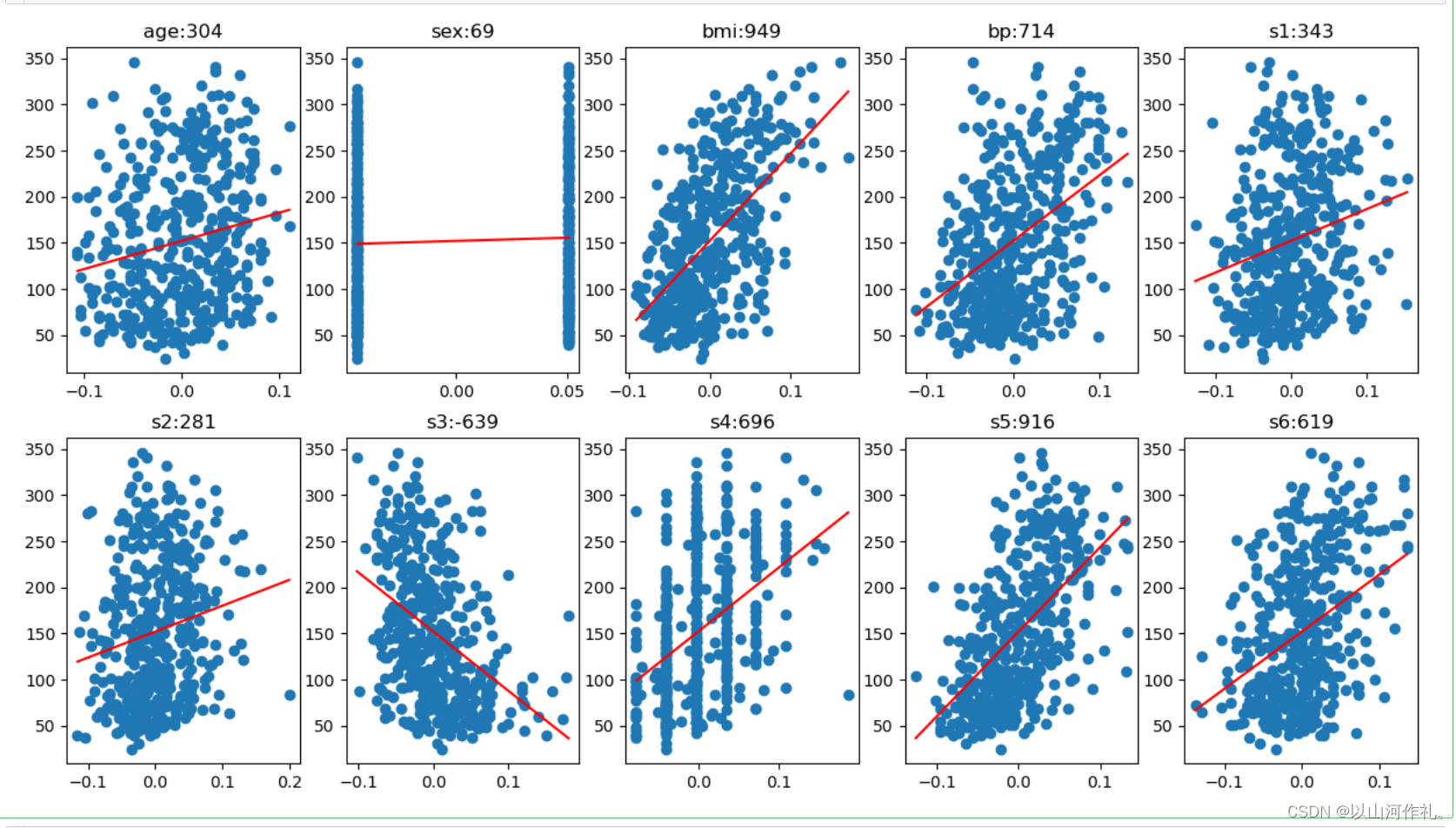
绘制一个包含10个子图的图表,每个子图显示一个特征与目标变量之间的关系
# 画子图
# 10个
# 2行五列
plt.figure(figsize=(15, 8))
for i, col in enumerate(df.columns):data = df[col]# display(data)# 画子图ax = plt.subplot(2, 5, i + 1)ax.scatter(data, target)# 线性回归linear = LinearRegression()linear.fit(df[[col]], target)# 训练后得到w,b的值w = linear.coef_# print(w)b = linear.intercept_# print(b)#画预测的直线 :y = wx+bx = np.array([data.min(), data.max()])y = w * x + bax.plot(x,y,c='r')# 标题ax.set_title(f'{col}:{int(w[0])}')
10.结果
从以上分析可知,单独看所有特征的训练结果,并不没有得到有效信息,我们拆分各个特征与指标的关系,可以看出:
bmi与糖尿病的相关性非常高,bp也有一定的关系,但是是否是直接关系,还是间接关系,有待深入考察。其他血清指标多少都和糖尿病有些关系,有的相关性强,有的相关性弱。
六·波士顿房价预测
1.前言
回归分析是一种统计学方法,用于研究变量之间的关系,特别是一个或多个自变量(解释变量)对因变量(响应变量)的影响。
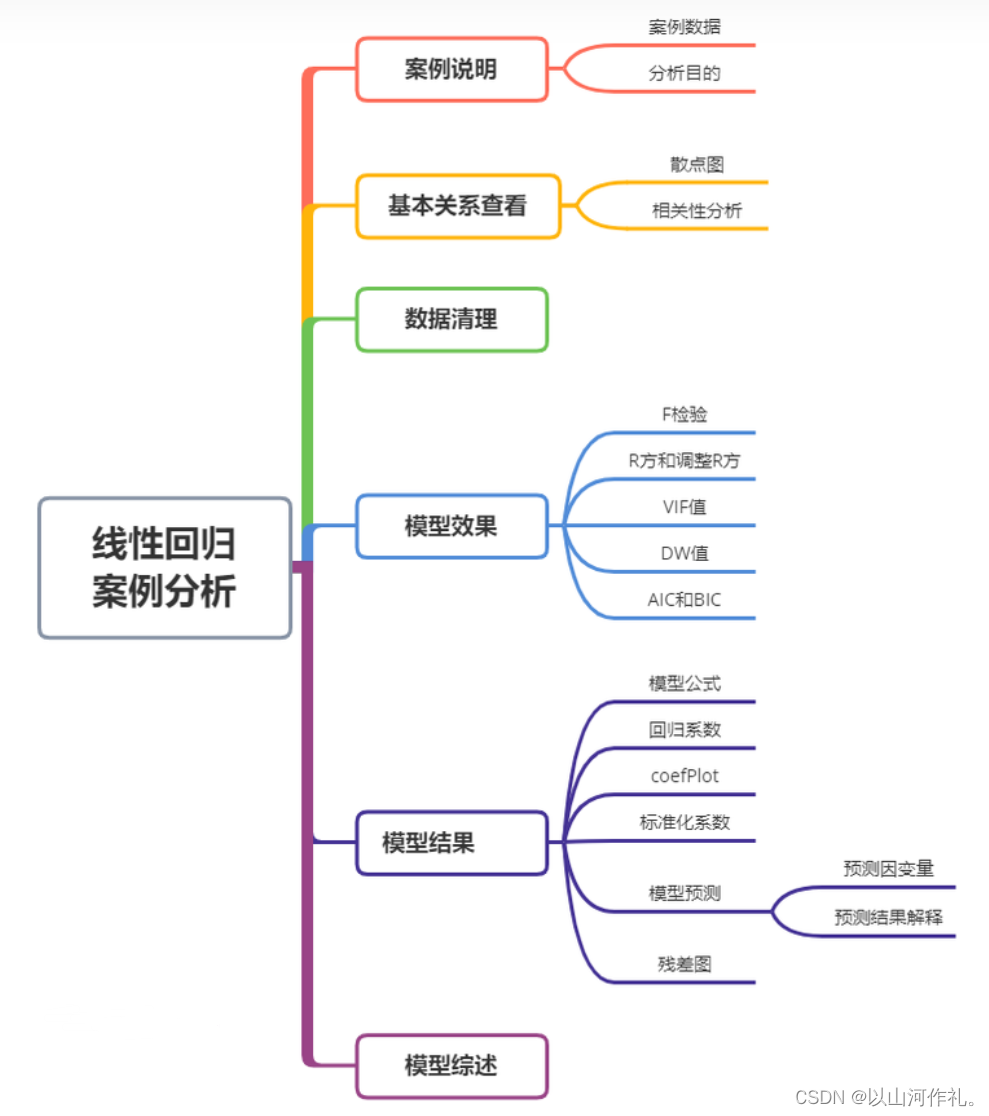
目前回归分析的研究范围可以分为如下几个部分组成:
线性回归:一元线性回归、多元线性回归和多个因变量与多个自变量的回归。
回归诊断:通过数据推断回归模型基本假设的合理性、基本假设不成立时对数据的修正、回归方程拟合效果的判断以及回归函数形式的选择。
回归变量的选择:根据什么标准选择自变量和逐步回归分析方法。
参数估计方法:偏最小二乘回归、主成分回归和岭回归。
非线性回归:一元非线性回归、分段回归和多元非线性回归。
定性变量的回归:因变量含有定性变量和自变量含有定性变量。
2.数据说明
波士顿房价数据说明:此数据源于美国某经济学杂志上,分析研究波士顿房价( Boston HousePrice)的数据集。数据集中的每一行数据都是对波士顿周边或城镇房价的情况描述,下面对数据集变量说明下,方便大家理解数据集变量代表的意义。
CRIM: 城镇人均犯罪率
ZN: 住宅用地所占比例
INDUS: 城镇中非住宅用地所占比例
CHAS: 虚拟变量,用于回归分析
NOX: 环保指数
RM: 每栋住宅的房间数
AGE: 1940 年以前建成的自住单位的比例
DIS: 距离 5 个波士顿的就业中心的加权距离
RAD: 距离高速公路的便利指数
TAX: 每一万美元的不动产税率
PTRATIO: 城镇中的教师学生比例
B: 城镇中的黑人比例
LSTAT: 地区中有多少房东属于低收入人群
MEDV: 自住房屋房价中位数(也就是均价)
首先对数据分析,处理特殊异常值,然后才是模型和评估,并应用模型进行预测。
3.数据导入
1.首先导入数据集,对数据进行分析
#导入Python常用数据分析的库import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set() #设置画图空间为 Seaborn 默认风格names=['CRIM','ZN','INDUS','CHAS','NOX','RM','GE','DIS','RAD','TAX','PRTATIO','B','LSTAT','PRICE']boston=pd.read_csv("/Users/glenji/Desktop/housing.csv",names=names,delim_whitespace=True)
boston.head(10)
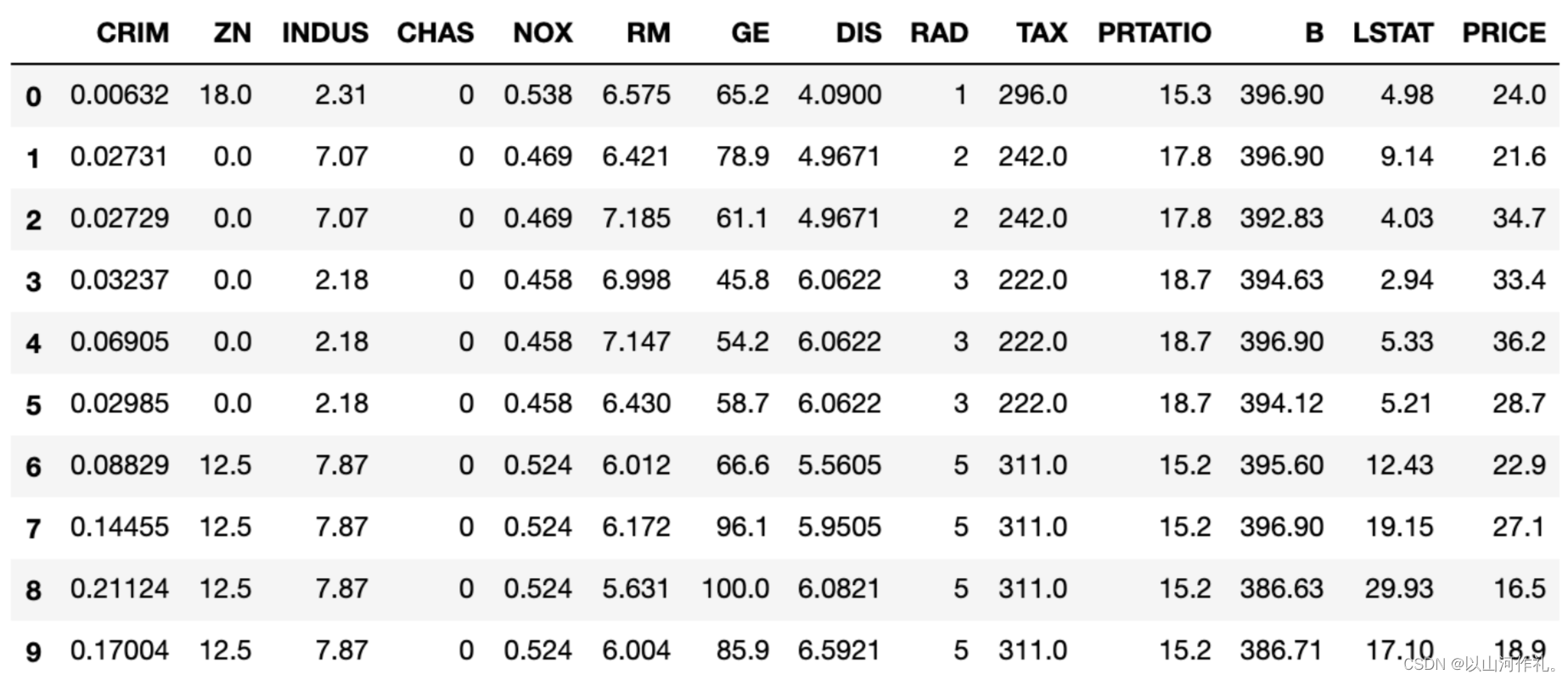
4.查看数据
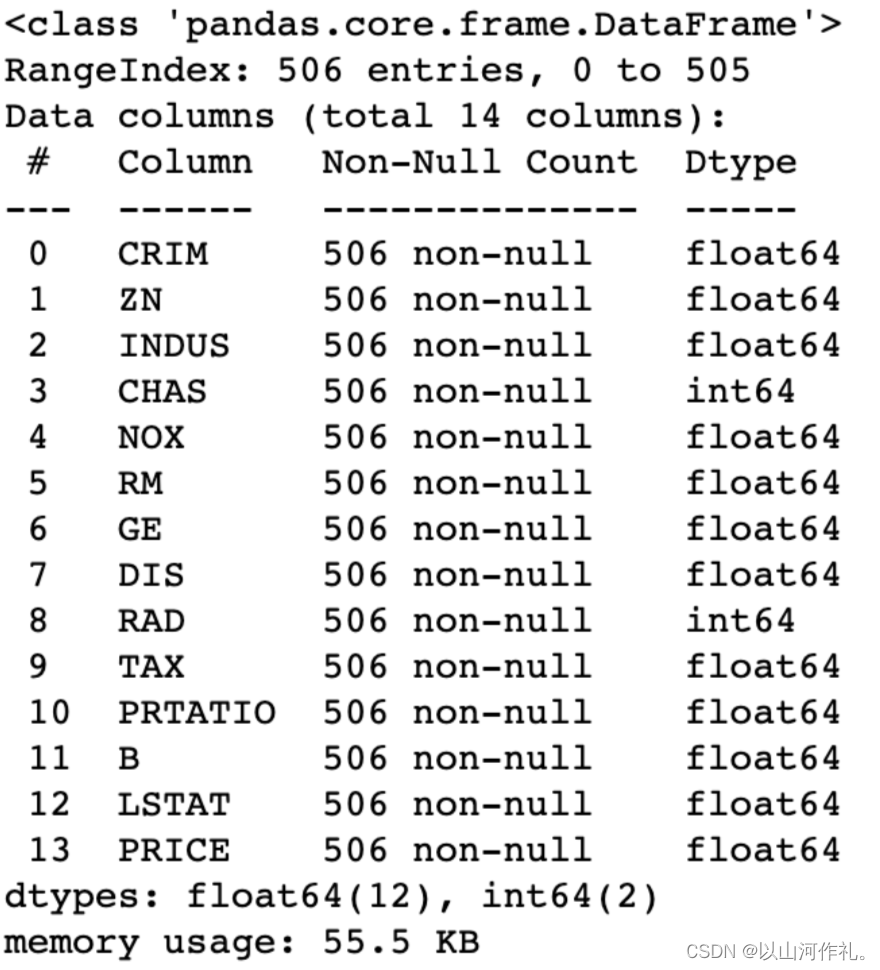
查看各字段基础信息:
boston.info()
5.查看缺失值
#查看缺失值boston.isnull().sum()
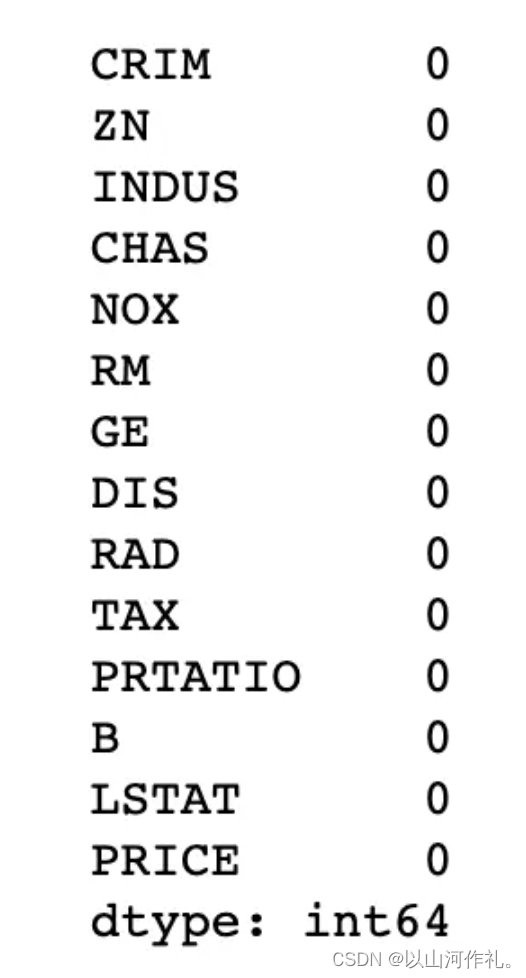
6.描述性数据分析
①查看描述性数据统计:可以看到各个字段的均值、中位数、标准差等。
描述性数据统计
boston.describe()
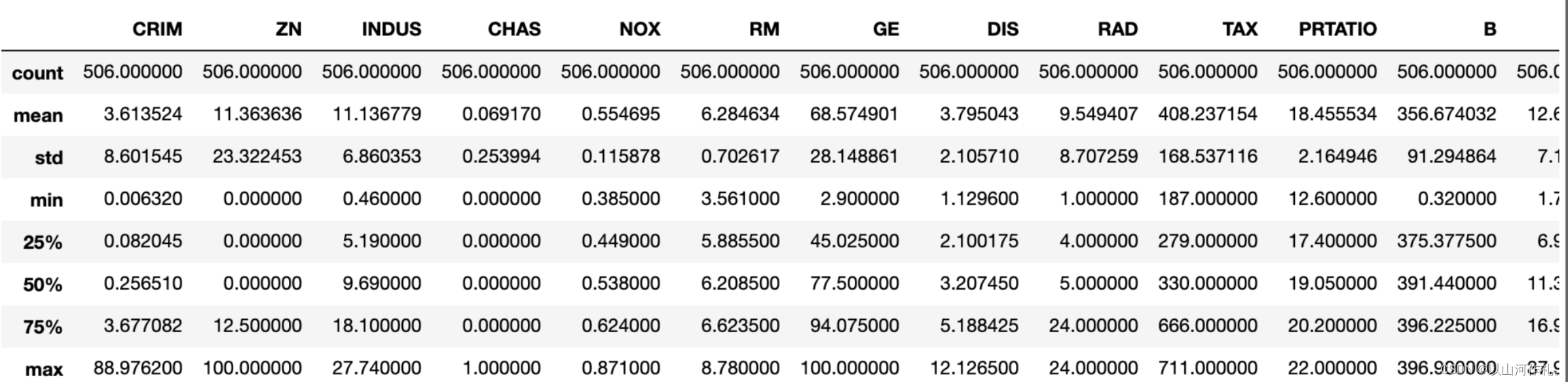
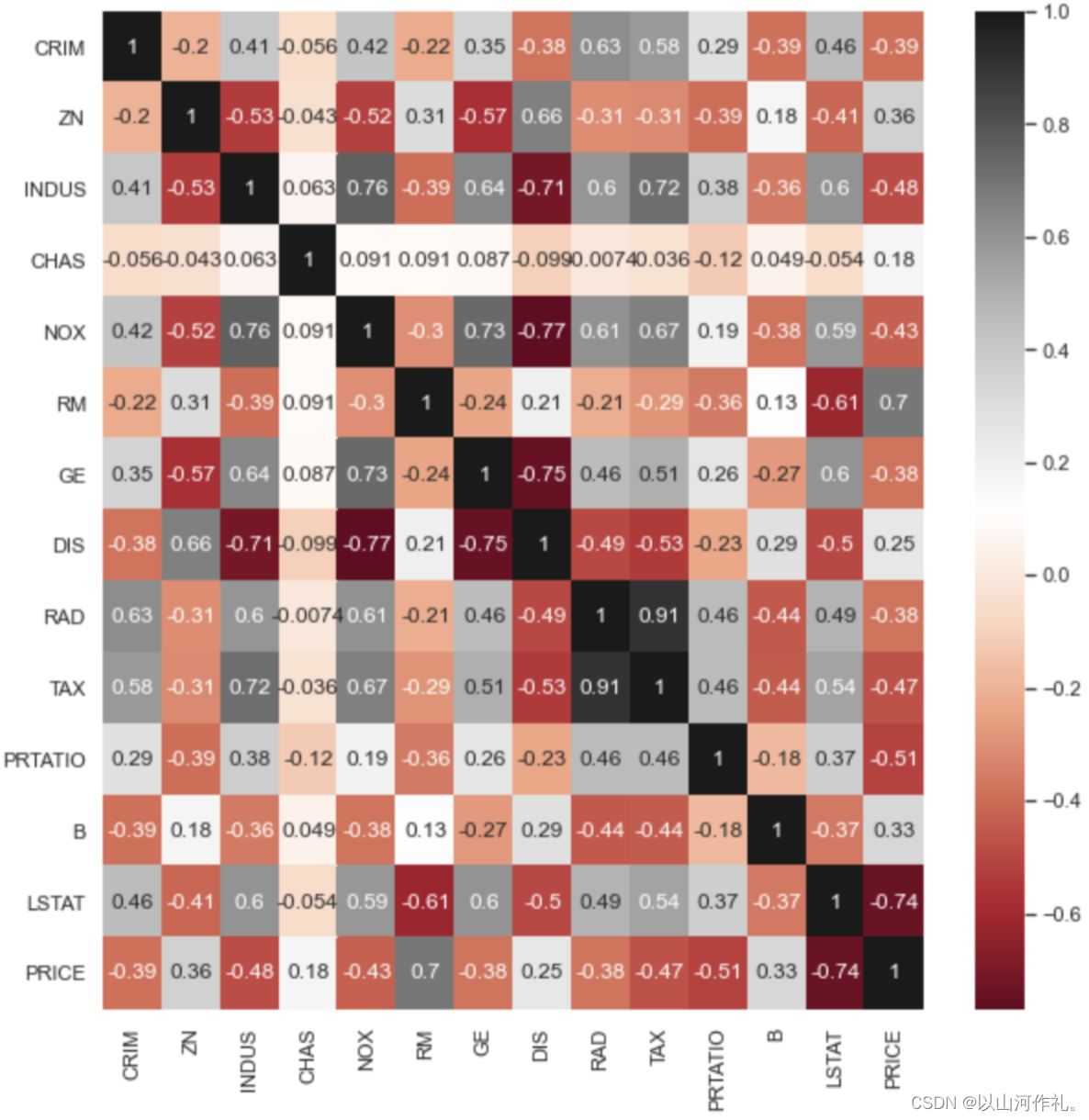
查看各字段的相关性:可以看到房子价格跟住宅的房间数成比较强的正相关,而跟低收入人数比例有比较强的负相关。
#查看相关性corrboston = boston.corr()
corrbostonplt.figure(figsize=(10,10)) #设置画布
sns.heatmap(corrboston,annot=True,cmap='RdGy')
plt.show()
查看是否穿过查尔斯河对房价的影响:可以看到被河流穿过的豪宅仅占比6.92%,而被查尔斯河穿过的豪宅,比没有被穿过的豪宅平均贵了28.7%。
#查看是否穿过查尔斯河的两类占比
#可以看到被河流穿过的豪宅仅占比6.92%fig,ax = plt.subplots(1,2,figsize=(10,5))boston['CHAS'].value_counts().plot.pie(ax=ax[0],shadow=False,autopct='%1.2f%%')
ax[0].set_ylabel('') #设置y轴标签
ax[0].set_xlabel('CHAS') #设置x轴标签sns.countplot('CHAS',data=boston,ax=ax[1])
ax[1].set_ylabel('')
ax[1].set_xlabel('CHAS')
plt.show()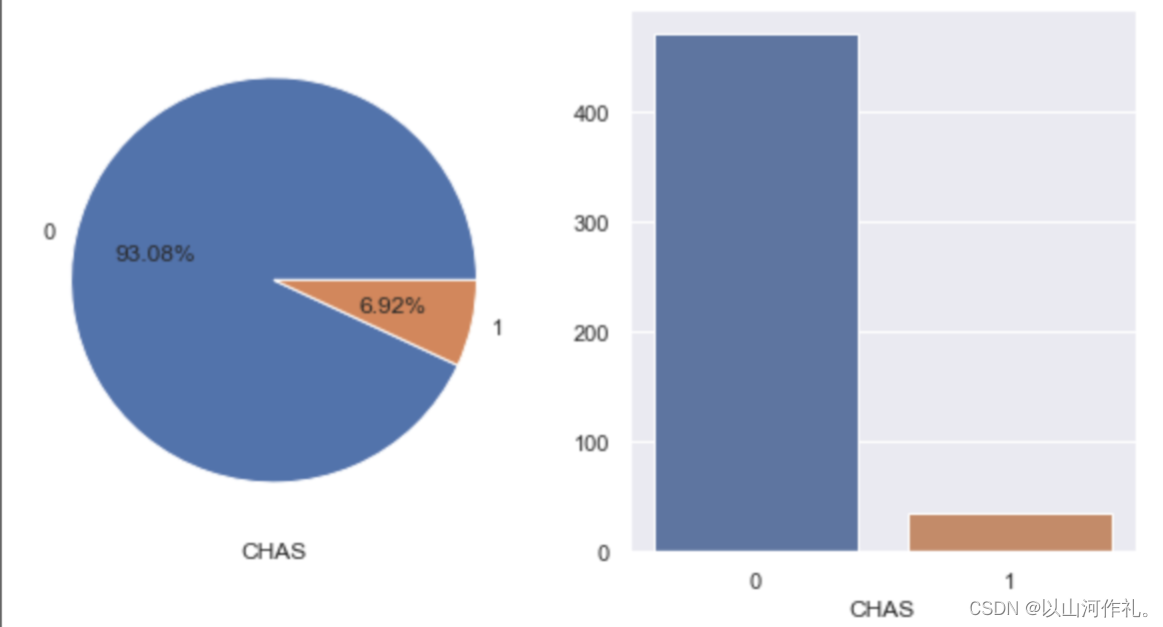
#再来看看两种不同类型的房子的价值如何
#可以看到被查尔斯河穿过的豪宅,比没有被穿过的豪宅平均贵了28.7%bostonCHAS = boston[['CHAS','PRICE']] #先将CHAS和PRICE两列数据取出bostonCHAS1=bostonCHAS.pivot_table(values='PRICE', #计算的值index='CHAS', #透视的行,分组的依据aggfunc='mean') #聚合函数# 对透视表进行降序排列
bostonCHAS1 = bostonCHAS1.sort_values(by='PRICE', # 排序依据ascending=False # 是否升序排列)bostonCHAS1

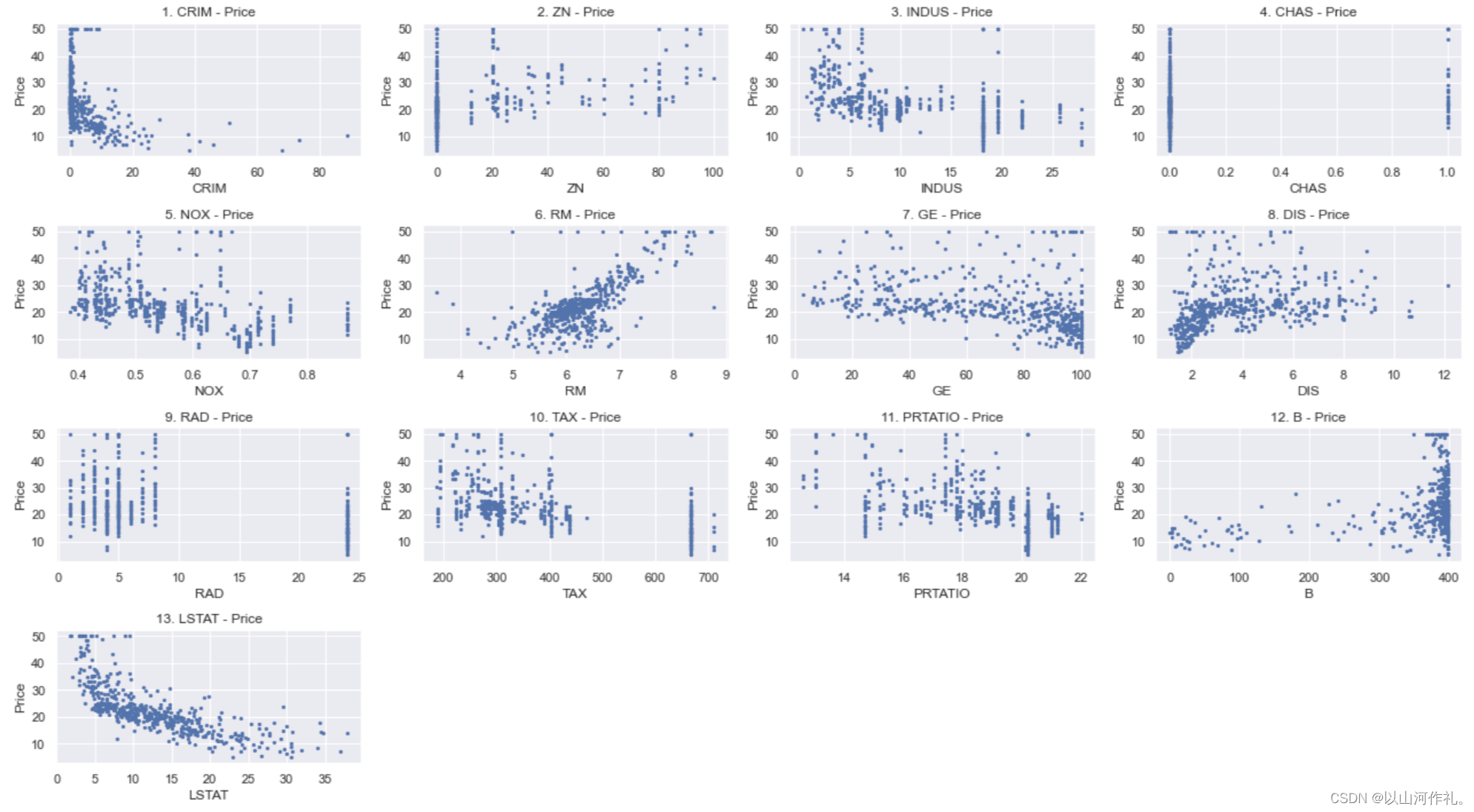
④看看各个字段与价格的散点图:以初步了解价格与相应字段的关系。可以看到不是所有的字段与价格都有较强的相关关系,但本例中不涉及多元线性回归的向后删除,仅做最简单的多元性性回归的分析处理。
x_data = boston[['CRIM','ZN','INDUS','CHAS','NOX','RM','GE','DIS','RAD','TAX','PRTATIO','B','LSTAT']] # 导入所有特征变量
y_data = boston[['PRICE']] # 导入目标值(房价)plt.figure(figsize=(18,10))for i in range(13):plt.subplot(4,4,i+1)plt.scatter(x_data.values[:,i],y_data,s = 5) #.values将DataFrame对象X_df转成ndarray数组plt.xlabel(names[i])plt.ylabel('Price')plt.title(str(i+1)+'. '+names[i]+' - Price') plt.tight_layout()
plt.show()
7.预测性数据分析
①选取线性回归字段:
from sklearn import linear_model#定义线性回归的x和y变量
x=pd.DataFrame(boston[['CRIM','ZN','INDUS','CHAS','NOX','RM','GE','DIS','RAD','TAX','PRTATIO','B','LSTAT']])
y=boston['PRICE']x
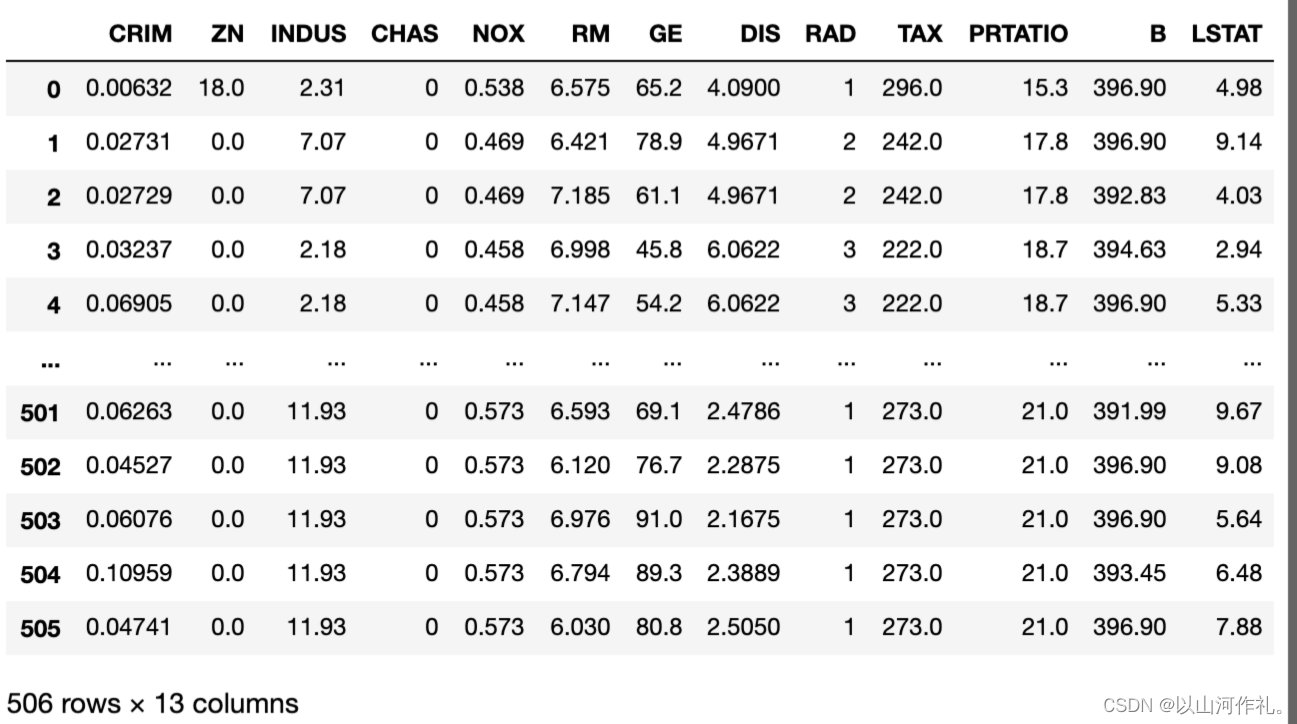
②建立线性回归模型,并调用:可以看到各个字段的回归系数,可以写出一个回归方程:y=ax1+bx2+……,理论上你知道一套新房子的各个字段,带入公式即可预测出价格。
#建立线性回归模型,并将变量带入模型进行训练。
clf = linear_model.LinearRegression()
clf.fit(x, y)#查看回归系数。本例为一元回归,所以只有一个系数。
print('回归系数:', clf.coef_)

③计算回归系数:计算出的回归系数为0.74,回归拟合效果较好。
from sklearn.metrics import r2_score
score = r2_score(y, y_pred)
score

8.预测
④可以进行简单的预测:
y_pred =clf.predict(x)
print(y_pred)