题目链接
[CSP-S2020] 函数调用
题目描述
函数是各种编程语言中一项重要的概念,借助函数,我们总可以将复杂的任务分解成一个个相对简单的子任务,直到细化为十分简单的基础操作,从而使代码的组织更加严密、更加有条理。然而,过多的函数调用也会导致额外的开销,影响程序的运行效率。
某数据库应用程序提供了若干函数用以维护数据。已知这些函数的功能可分为三类:
- 将数
- 将数据中的每一个元素乘以一个相同值;
- 依次执行若干次函数调用,保证不会出现递归(即不会直接或间接地调用本身)。
在使用该数据库应用时,用户可一次性输入要调用的函数序列(一个函数可能被调用多次),在依次执行完序列中的函数后,系统中的数据被加以更新。某一天,小 A 在应用该数据库程序处理数据时遇到了困难:由于频繁而低效的函数调用,系统在执行操作时进入了无响应的状态,他只好强制结束了数据库程序。为了计算出正确数据,小 A 查阅了软件的文档,了解到每个函数的具体功能信息,现在他想请你根据这些信息帮他计算出更新后的数据应该是多少。
输入格式
第一行一个正整数 n n n,表示数据的个数。
第二行 n n n 个整数,第 i i i 个整数表示下标为 i i i 的数据的初始值为 a i a_i ai。
第三行一个正整数 m m m,表示数据库应用程序提供的函数个数。函数从 1 ∼ m 1 \sim m 1∼m 编号。
接下来 m m m 行中,第 j j j( 1 ≤ j ≤ m 1 \le j \le m 1≤j≤m)行的第一个整数为 T j T_j Tj,表示 j j j 号函数的类型:
- 若 T j = 1 T_j = 1 Tj=1,接下来两个整数 P j , V j P_j, V_j Pj,Vj 分别表示要执行加法的元素的下标及其增加的值;
- 若 T j = 2 T_j = 2 Tj=2,接下来一个整数 V j V_j Vj 表示所有元素所乘的值;
- 若 T j = 3 T_j = 3 Tj=3,接下来一个正整数 C j C_j Cj 表示 j j j 号函数要调用的函数个数,
随后 C j C_j Cj 个整数 g 1 ( j ) , g 2 ( j ) , … , g C j ( j ) g^{(j)}_1, g^{(j)}_2, \ldots , g^{(j)}_{C_j} g1(j),g2(j),…,gCj(j) 依次表示其所调用的函数的编号。
第 m + 4 m + 4 m+4 行一个正整数 Q Q Q,表示输入的函数操作序列长度。
第 m + 5 m + 5 m+5 行 Q Q Q 个整数 f i f_i fi,第 i i i 个整数表示第 i i i 个执行的函数的编号。
输出格式
一行 n n n 个用空格隔开的整数,按照下标 1 ∼ n 1 \sim n 1∼n 的顺序,分别输出在执行完输入的函数序列后,数据库中每一个元素的值。答案对 998244353 \boldsymbol{998244353} 998244353 取模。
样例 #1
样例输入 #1
3
1 2 3
3
1 1 1
2 2
3 2 1 2
2
2 3
样例输出 #1
6 8 12
样例 #2
样例输入 #2
10
1 2 3 4 5 6 7 8 9 10
8
3 2 2 3
3 2 4 5
3 2 5 8
2 2
3 2 6 7
1 2 5
1 7 6
2 3
3
1 2 3
样例输出 #2
36 282 108 144 180 216 504 288 324 360
提示
【样例 #1 解释】
1 1 1 号函数功能为将 a 1 a_1 a1 的值加一。 2 2 2 号函数功能为所有元素乘 2 2 2。 3 3 3 号函数将先调用 1 1 1 号函数,再调用 2 2 2 号函数。
最终的函数序列先执行 2 2 2 号函数,所有元素的值变为 2 , 4 , 6 2, 4, 6 2,4,6。
再执行 3 3 3 号函数时,先调用 1 1 1 号函数,所有元素的值变为 3 , 4 , 6 3, 4, 6 3,4,6。再调用 2 2 2 号函数,所有元素的值变为 6 , 8 , 12 6, 8, 12 6,8,12。
【数据范围】
| 测试点编号 | n , m , Q ≤ n, m, Q \le n,m,Q≤ | ∑ C j \sum C_j ∑Cj | 其他特殊限制 |
|---|---|---|---|
| 1 ∼ 2 1 \sim 2 1∼2 | 1000 1000 1000 | = m − 1 = m - 1 =m−1 | 函数调用关系构成一棵树 |
| 3 ∼ 4 3 \sim 4 3∼4 | 1000 1000 1000 | ≤ 100 \le 100 ≤100 | 无 |
| 5 ∼ 6 5 \sim 6 5∼6 | 20000 20000 20000 | ≤ 40000 \le 40000 ≤40000 | 不含第 2 2 2 类函数或不含第 1 1 1 类函数 |
| 7 7 7 | 20000 20000 20000 | = 0 = 0 =0 | 无 |
| 8 ∼ 9 8 \sim 9 8∼9 | 20000 20000 20000 | = m − 1 = m - 1 =m−1 | 函数调用关系构成一棵树 |
| 10 ∼ 11 10 \sim 11 10∼11 | 20000 20000 20000 | ≤ 2 × 1 0 5 \le 2 \times 10^5 ≤2×105 | 无 |
| 12 ∼ 13 12 \sim 13 12∼13 | 1 0 5 10^5 105 | ≤ 2 × 1 0 5 \le 2 \times 10^5 ≤2×105 | 不含第 2 2 2 类函数或不含第 1 1 1 类函数 |
| 14 14 14 | 1 0 5 10^5 105 | = 0 = 0 =0 | 无 |
| 15 ∼ 16 15 \sim 16 15∼16 | 1 0 5 10^5 105 | = m − 1 = m - 1 =m−1 | 函数调用关系构成一棵树 |
| 17 ∼ 18 17 \sim 18 17∼18 | 1 0 5 10^5 105 | ≤ 5 × 1 0 5 \le 5 \times 10^5 ≤5×105 | 无 |
| 19 ∼ 20 19 \sim 20 19∼20 | 1 0 5 10^5 105 | ≤ 1 0 6 \le 10^6 ≤106 | 无 |
对于所有数据: 0 ≤ a i ≤ 1 0 4 0 \le a_i \le 10^4 0≤ai≤104, T j ∈ { 1 , 2 , 3 } T_j \in \{1,2,3\} Tj∈{1,2,3}, 1 ≤ P j ≤ n 1 \le P_j \le n 1≤Pj≤n, 0 ≤ V j ≤ 1 0 4 0 \le V_j \le 10^4 0≤Vj≤104, 1 ≤ g k ( j ) ≤ m 1 \le g^{(j)}_k \le m 1≤gk(j)≤m, 1 ≤ f i ≤ m 1 \le f_i \le m 1≤fi≤m。
算法思想
根据题目描述,输入一个函数操作的序列,输出执行完输入的函数序列后,数据库中每一个元素的值。
在所有的函数序列中,一共包含 3 3 3种操作类型:
- 加法操作,对于指定下标的元素增加一个数值值;
- 乘法操作,给所有元素乘上一个数值;
- 嵌套调用,以一定顺序调用其它函数。
乘法和加法
对于乘法操作,只需要统计对所有变量所乘的值 V V V,在最后给每个元素乘上就可以了。
对于加法操作,会受到后面乘法操作的影响。假设整个数据库中只有一个元素 x x x,对它依次执行: + 1 、 × 2 、 + 3 、 × 4 +1、\times2、+3、\times4 +1、×2、+3、×4操作,如下图所示:

那么 + 1 +1 +1的操作实际上就有了一个 2 × 4 2\times4 2×4的系数, + 3 +3 +3的操作系数为 4 4 4;那 x x x最终会变为 8 x + 8 × 1 + 4 × 3 8x+8\times1+4\times3 8x+8×1+4×3。
也就是说加法操作最终对答案的贡献等于它后面所有乘法操作的乘积 × \times ×加上的数。
这样就可以从后向前进行函数操作,记录已进行的乘法操作的乘积,就能计算出每次加法操作的所要乘的系数了。
这里所要乘的系数可以理解为加法被执行的次数。
嵌套调用
对于所有操作3,按顺序向它调用的函数连边,会得到一个有向无环图(DAG)。
对于图上的每个点(代表着一种操作),维护一个mul属性,表示执行这个操作会给每个元素乘上的值。
- 加法操作的
mul为 1 1 1 - 乘法操作的
mul为它要乘上的数 v v v。 - 嵌套操作的
mul等于它直接相邻的所有点的mul的乘积,如下图所示 f i f_i fi的mul为 2 × 4 = 8 2\times4=8 2×4=8
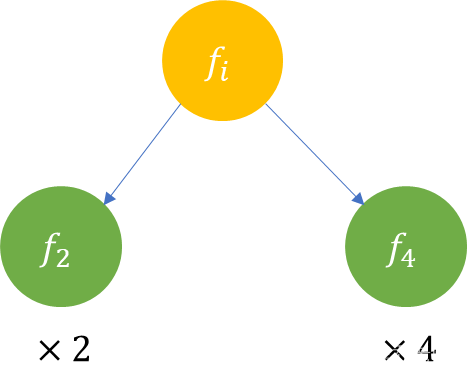
可以对拓扑序列从后向前遍历一次,来求嵌套操作的mul。
但是有些嵌套操作既包含加法又包含乘法,该如何计算其中的加法操作所要乘的系数呢?如下图所示
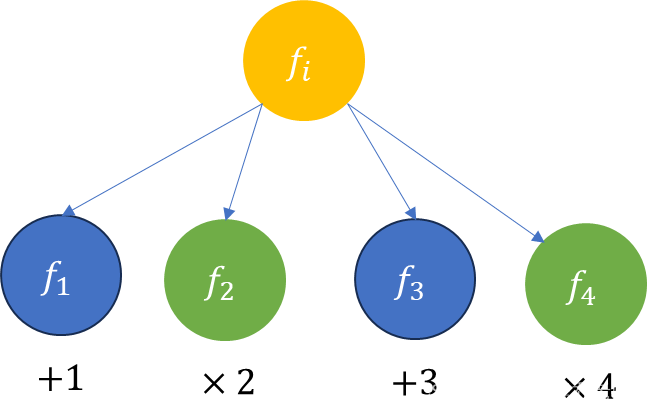
可以发现, f 1 f_1 f1的所要乘的系数(加法被执行的次数)跟两部分有关:
- 嵌套函数 f i f_i fi的执行次数
对每个点再维护一个sum属性,表示加法或嵌套函数被执行的次数。然后从后向前遍历操作序列,就可以求得 f i f_i fi的执行次数, - f 1 f_1 f1后面所有乘法操作的乘积,例如 f 2 f_2 f2, f 4 f_4 f4
可以倒序枚举 f 1 f_1 f1的所有邻点,从后向前统计出 f 2 f_2 f2和 f 4 f_4 f4的mul。
那么, f 1 . s u m = f i . s u m × f 2 . m u l × f 4 . m u l f_1.sum=f_i.sum\times f_2.mul\times f_4.mul f1.sum=fi.sum×f2.mul×f4.mul
最后,让数组的每个元素乘上所有 Q Q Q 次操作的mul,再遍历所有加法操作计算应该加多少即可。
代码实现
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1e5 + 5, M = 1e6 + 5, mod = 998244353;
struct F
{//mul表示执行函数时所有变量需要乘的值是多少//sum表示函数一共的执行次数int t, p, v, mul, sum;
}f[N];
int n, m, Q, a[N], d[N], q[N], g[N];
int h[N], e[M], ne[M], idx;
void add(int a, int b) // 添加一条边a->b
{e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void topsort()
{int hh = 0, tt = -1;for (int i = 1; i <= m; i ++ )if (!d[i]) // d[i] 存储点i的入度q[ ++ tt] = i;while (hh <= tt){int t = q[hh ++ ];for (int i = h[t]; ~ i; i = ne[i]){int j = e[i];if (-- d[j] == 0)q[ ++ tt] = j;}}
}
void get_mul()
{for(int i = m - 1; i >= 0; i --) //从后向前遍历拓扑序列{int u = q[i]; //u函数的mul等于其子函数mul的乘积for(int j = h[u]; ~ j; j = ne[j]){int v = e[j];f[u].mul = (LL)f[u].mul * f[v].mul % mod; }}
}
void get_sum()
{for(int i = 0; i < m; i ++)//从前向后遍历拓扑序列{int u = q[i], sum = f[u].sum;for(int j = h[u]; ~ j; j = ne[j]){int v = e[j];//u的子函数的执行次数包含两部分f[v].sum = (f[v].sum + sum) % mod; //u的执行次数sum = (LL) sum * f[v].mul % mod; //v后面累积乘的值}}
}int main()
{scanf("%d", &n);for(int i = 1; i <= n; i ++) scanf("%d", &a[i]);scanf("%d", &m);memset(h, -1, sizeof h);for(int i = 1; i <= m; i ++){scanf("%d", &f[i].t);if(f[i].t == 1) scanf("%d%d", &f[i].p, &f[i].v);else if(f[i].t == 2) scanf("%d", &f[i].v);else //嵌套函数{int c, v;scanf("%d", &c);while(c --) { scanf("%d", &v); d[v] ++; add(i, v); }}}for(int i = 1; i <= m; i ++) //初始化函数的mul属性if(f[i].t == 2) f[i].mul = f[i].v; //乘法的mul为velse f[i].mul = 1; //加法或者嵌套函数的mul为1topsort(); //拓扑排序get_mul(); //根据拓扑序列计算乘法的贡献scanf("%d", &Q);for(int i = 1; i <= Q; i ++) scanf("%d", &g[i]);//输入调用序列int sum = 1; //计算所有乘法累积所乘的值for(int i = Q; i > 0; i --) //从后向前遍历调用序列{int u = g[i];f[u].sum = (f[u].sum + sum) % mod; //累加乘法对加法的影响sum = (LL)sum * f[u].mul % mod; //累积所乘的值}get_sum(); //根据拓扑序列,计算加法的贡献for(int i = 1; i <= n; i ++) //计算乘法操作最终对每个元素的影响a[i] = (LL)a[i] * sum % mod; for(int i = 1; i <= m; i ++) //计算加法操作最终对每个元素的影响if(f[i].t == 1)a[f[i].p] = (a[f[i].p] + (LL)f[i].v * f[i].sum) % mod;for(int i = 1; i <= n; i ++)printf("%d ", a[i]);return 0;
}