单元最短路模板 dijkstra以及SPFA的FAQ-编程知识

单元最短路模板 dijkstra以及SPFA的FAQ

单源最短路

首先先看两道题目：
Luogu P3371 【模板】单源最短路径（弱化版）
Luogu P4779 【模板】单源最短路径（标准版）
两道题目都是求最小单元最短路。
使用Dijkstra两道题目均可以通过，但是如果使用SPFA则只能通过Luogu P3371。

SPFA

依据Bellman-Ford算法，其在计算过程中，保证BFS队列中不会出现两个相同的元素，其复杂度为 $O (q m)$ ，其中 $q$ 为每个节点的平均入队次数，已经有人证明最坏情况下复杂度为 $O (nm)$ 与Bellman-Ford算法复杂度相同，但是在随机数据情况下速度快于Bellman-Ford，与Bellman-Ford都可以处理边权有负数的情况。

Dijkstra

不能处理边权为负数的情况复杂度 $O (m l o g n)$ （也有说 $O (m l o g m)$ 的）。其原理是每次选择当前最短路最小的且没有选择过的点将其与其邻近点做松弛操作。

性质1：在选择某个点与其邻近点做松弛操作时能够保证当前选择的点的最短路已经求出。

正是性质1保证了Dijkstra算法的正确性。

正是性质1保证了Dijkstra算法过程中每个点只会选择一次。

正是性质1保证了Dijkstra算法的复杂度。

Dijkstra算法与负权边

如果存在负权边，那么性质1可能会被破坏，从而导致Dijkstra算法不能得到正确的结果，一个常见的例子如下：
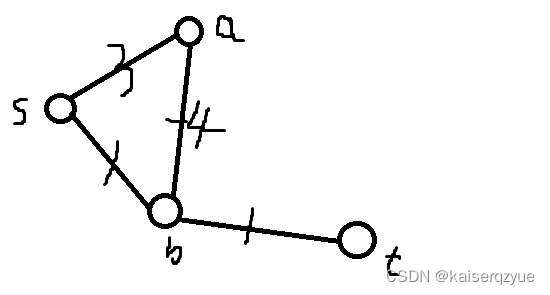
在这里插入图片描述
从s出发，计算出d[a]=3, d[b]=1，这时候会选择b进行下一次邻近点的松弛操作，明显发现此时d[b]=1并不是从s到达b的最短路（应该为s->a->b），因此性质1被破坏（正是因为存在负权边导致性质1不能得到保证），Dijkstra算法后续过程中会出现错误。

这也是为什么Dijkstra算法中需要使用used数组来标识某个点是否已经被选择，常见的堆优化Dijkstra算法大致如下：

q.push({0, s});
dis[s] = 0;
while (!q.empty()) {auto item = q.top();q.pop();int u = item.second;if (used[u]) { continue; }used[u] = true;for (auto edge : g[u]) {int v = edge.to, w = edge.w;if (dis[v] > dis[u] + w) {dis[v] = dis[u] + w;q.push({dis[v], v});}}
}

上面代码中used数组保证了每个点只被选择一次。

能否去掉每个点选择一次的限制

我们是否可以将used数组改成类似于SPFA里面的inq数组，也就是将上面的代码改成如下代码：

q.push({0, s});
inq[s] = 0;
while (!q.empty()) {auto item = q.top();q.pop();int u = item.second;inq[u] = false;for (auto edge : g[u]) {int v = edge.to, w = edge.w;if (dis[v] > dis[u] + w) {dis[v] = dis[u] + w;if (inq[v]) { continue; }inq[v] = true;q.push({dis[v], v});}}
}