掌握递归是解决许多编程问题的关键，尤其是那些涉及树形结构、组合问题、搜索问题等领域的题目。递归方法的核心在于将问题分解成更小的子问题，直到达到一个基本情况（base case），然后再逐层返回解决整个问题。理解和掌握递归，最好的方式是通过实践一系列逐渐增加难度的问题。

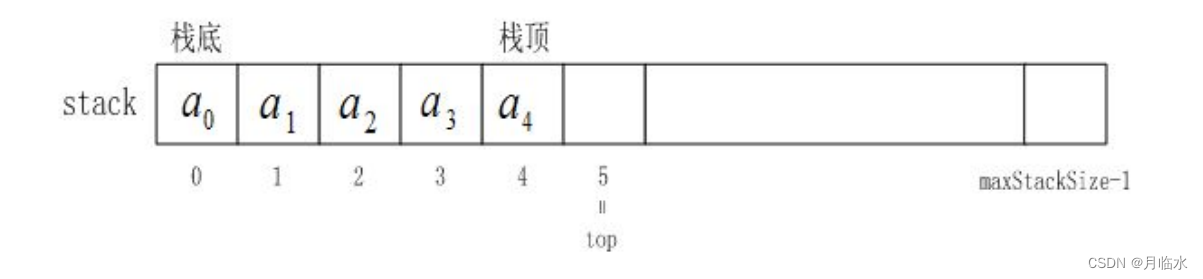
递归与栈的关系

递归的过程就是出入栈的过程

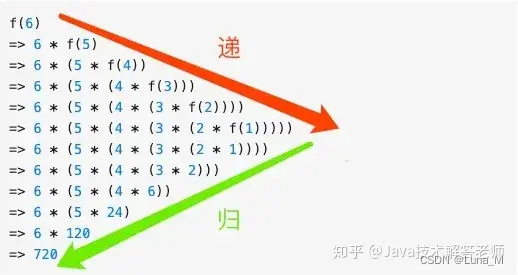
我们以阶乘为例：

def Factorial(n):if n == 0:return 1return factorial(n-1) * n

取 n=3，则过程如下：
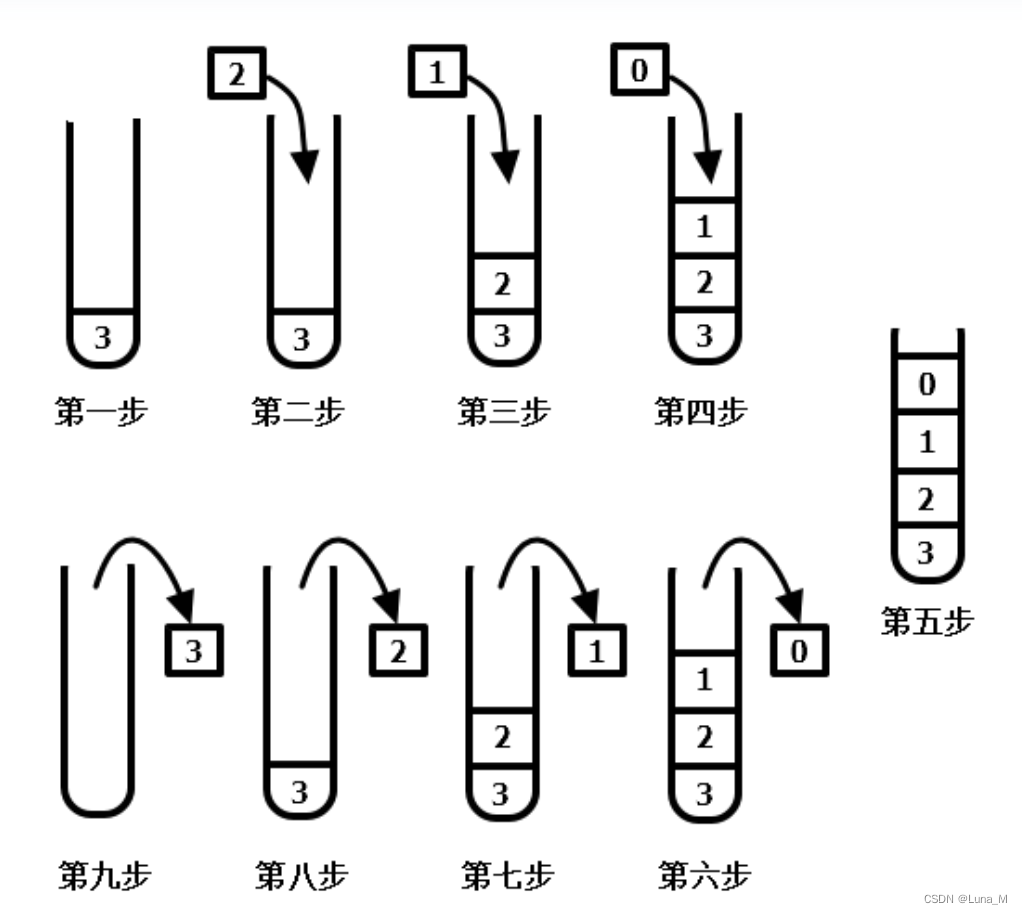第 1~4 步，都是入栈过程，Factorial(3)调用了Factorial(2)，Factorial(2)又接着调用Factorial(1)，直到Factorial(0)；
第 5 步，因 0 是递归结束条件，故不再入栈，此时栈高度为 4，即为我们平时所说的递归深度；
第 6~9 步，Factorial(0)做完，出栈，而Factorial(0)做完意味着Factorial(1)也做完，同样进行出栈，重复下去，直到所有的都出栈完毕，递归结束。

每一个递归程序都可以把它改写为非递归版本。我们只需利用栈，通过入栈和出栈两个操作就可以模拟递归的过程，二叉树的遍历无疑是这方面的代表。

如何思考递归

我们怎么判断这个递归计算是否是正确的呢？Paul Graham 提到一种方法，如下：

如果下面这两点是成立的，我们就知道这个递归对于所有的 n 都是正确的。· 当 n=0,1 时，结果正确；
· 假设递归对于 n 是正确的，同时对于 n+1 也正确。

这种方法很像数学归纳法，也是递归正确的思考方式，上述的第 1 点称为基本情况，第 2 点称为通用情况。

在递归中，我们通常把第 1 点称为终止条件，因为这样更容易理解，其作用就是终止递归，防止递归无限地运行下去。

下面我们用1个例子来具体说明这种数学归纳法：

汉诺塔

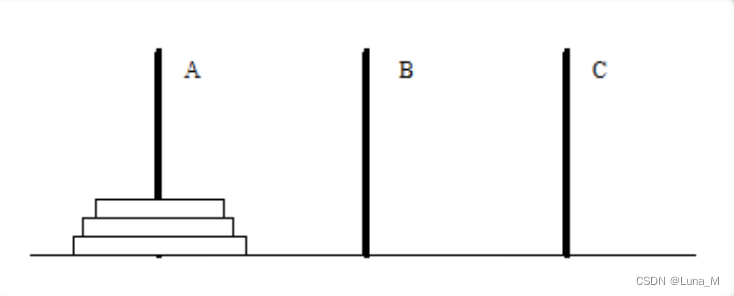问题描述为：有三根杆子 A，B，C。A 杆上有 N 个穿孔圆盘，盘的尺寸由上到下依次变大，B，C 杆为空。要求按下列规则将所有圆盘移至 C 杆：

• 每次只能移动一个圆盘；
• 大盘不能叠在小盘上面。

问：如何移？最少要移动多少次？

首先看下基本情况，即终止条件：N=1 时，直接从 A 移到 C。

再来看下通用情况：当有 N 个圆盘在 A 上，我们已经找到办法将其移到 C 杠上了，我们怎么移动 N+1 个圆盘到 C 杠上呢？很简单，我们首先用将 N 个圆盘移动到 C 上的方法将 N 个圆盘都移动到 B 上，然后再把第 N+1 个圆盘（最后一个）移动到 C 上，再用同样的方法将在 B 杠上的 N 个圆盘移动到 C 上，问题解决。

def Hanoi(n, a='A', b='B', c='C'):steps = 0if n == 0:return stepsif n==1:steps += 1print(a, '-->', c)return stepssteps += Hanoi(n-1,a,c,b)steps += Hanoi(1,a,b,c)steps += Hanoi(n-1,b,a,c)return steps

经典题目

入门：斐波那契数列

斐波那契数列是通过如下递归式定义的：

• F(0) = 0, F(1) = 1
• 对于 n > 1，F(n) = F(n-1) + F(n-2)

这意味着，斐波那契数列从0和1开始，之后的每个数字都是前两个数字的和。例如，斐波那契数列的前几个数字是：0, 1, 1, 2, 3, 5, 8, 13, 21…

def fib(n):if n<2:return nreturn  fib(n-1) + fib(n-2)

分治法：归并排序

归并排序是一种高效的排序算法，基于分治法的一个典型应用。它将一个数组分成两半，对每部分递归地应用归并排序，然后将两个排序好的部分合并成一个最终的排序数组。

步骤：

1. 分解：将当前区间一分为二，递归地对这两个子区间进行归并排序。
2. 合并：将两个排序好的子区间合并成一个最终的排序区间。

实现提示
归并过程需要额外的空间来合并两个有序数组，这是归并排序空间复杂度为O(n)的原因。
实现归并排序时，考虑如何优雅地合并两个有序的子数组。
双指针法

def merge_sort(arr):length = len(arr)if length <2:return arrmid = length//2left_half = arr[:mid]right_half = arr[mid:]left_sort = merge_sort(left_half)right_sort = merge_sort(right_half)i = j = k = 0while i < len(left_sort) and j < len(right_sort):if left_sort[i] <= right_sort[j]:arr[k] = left_sort[i]i += 1k += 1else:arr[k] = right_sort[j]j += 1k += 1if i < len(left_sort):arr[k:] = left_sort[i:]if j < len(right_sort):arr[k:] = right_sort[j:]return arr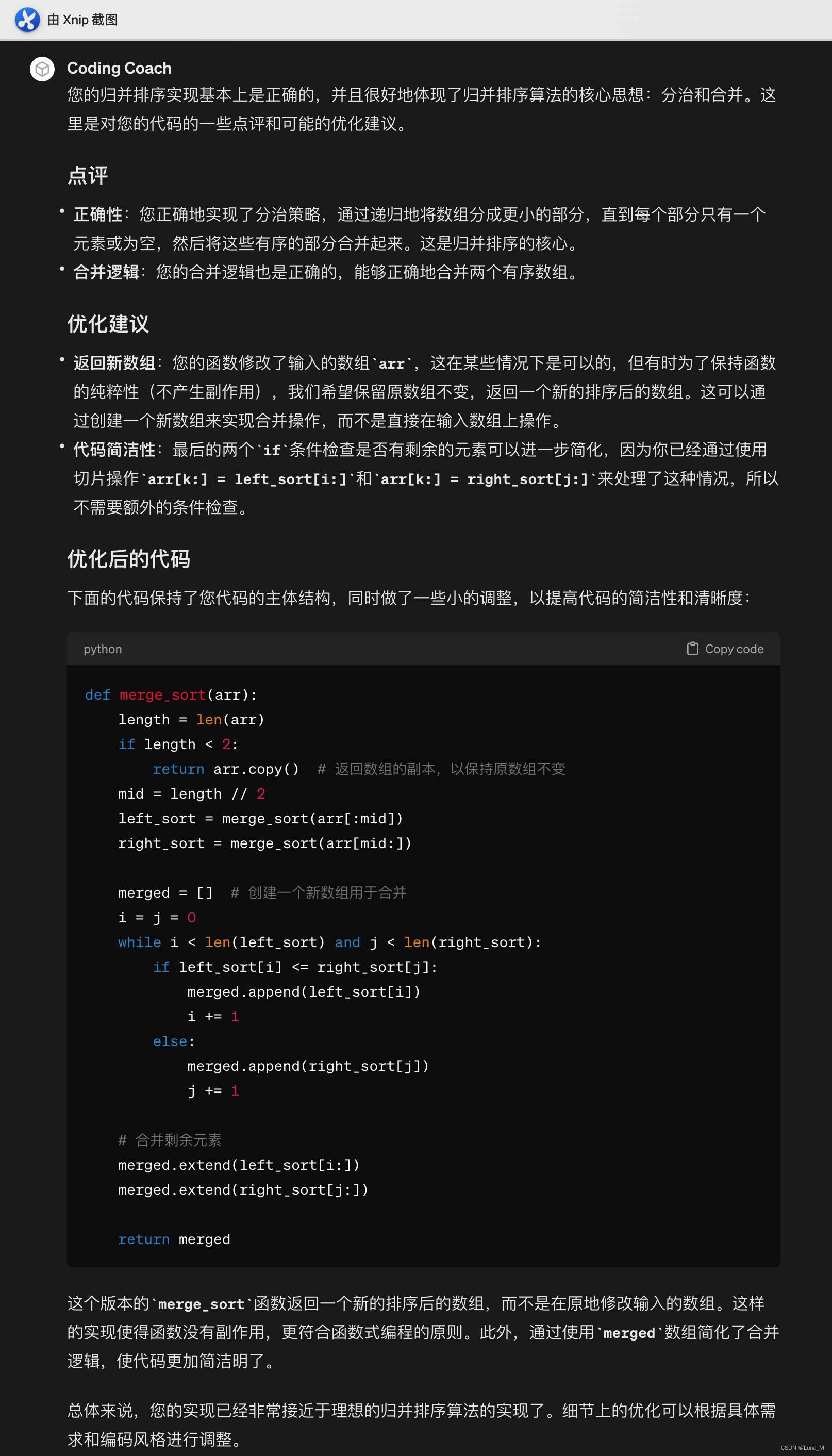

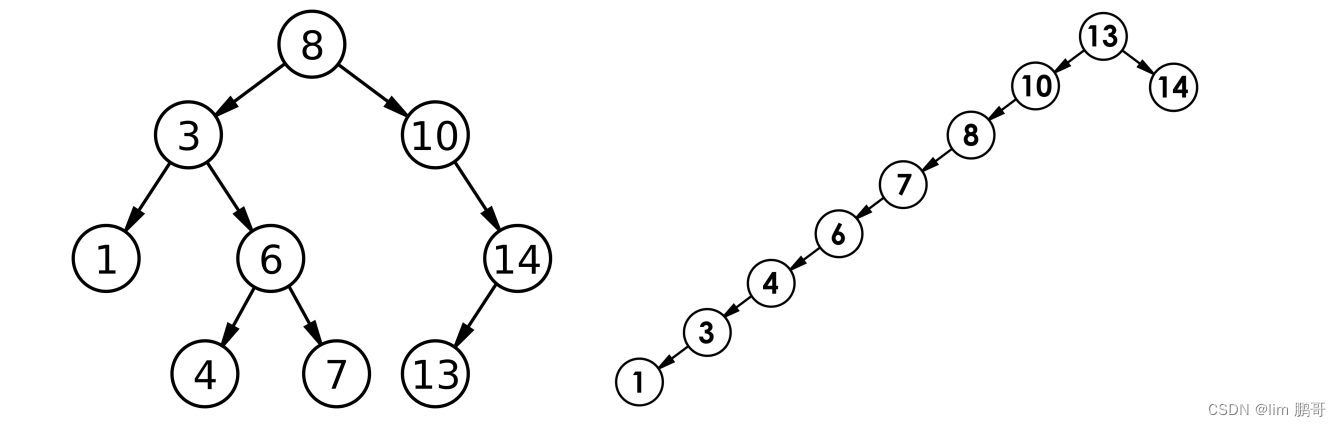
树的递归遍历

关于二叉树的深度优先所有（DFS）问题，我们在前面的文章中有详细的讲解。

前序遍历（Preorder Traversal）：首先访问根节点，然后递归地做前序遍历左子树，接着递归地做前序遍历右子树。
中序遍历（Inorder Traversal）：首先递归地做中序遍历左子树，然后访问根节点，最后递归地做中序遍历右子树。
后序遍历（Postorder Traversal）：首先递归地做后序遍历左子树，然后递归地做后序遍历右子树，最后访问根节点。

在Python中，二叉树节点可以通过下面的TreeNode类来表示：

class TreeNode:def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = right

def preorderTraversal(root):res = []if not root:return resres.append(root)res.extend(preorderTraversal(root.left))res.extend(preorderTraversal(root.right))return resdef inorderTraversal(root):res = []if not root:return resres.extend(inorderTraversal(root.left))res.append(root)res.extend(inorderTraversal(root.right))return resdef postorderTraversal(root):res = []if not root:return resres.extend(postorderTraversal(root.left))res.extend(postorderTraversal(root.right))res.append(root)return res

组合问题：子集

给定一组不同的整数，返回所有可能的子集（幂集）。解集不能包含重复的子集。

例子

输入:
nums = [1,2,3]

输出:

[  [3],[1],[2],[1,2,3],[1,3],[2,3],[1,2],[]
]

这个问题可以通过递归（回溯算法）来解决。我们之前的文章也讲到过回溯的理论基础和模板。本题的基本思路是遍历所有元素，对于每个元素，我们可以选择将其包含到当前子集中，或者不包含它。每当我们到达数组的末尾时，我们就找到了一个可能的子集，并将其添加到结果列表中。

def subsets(nums):res = []def backtrack(start, path):res.append(path[:])for i in range(start, len(nums)):path.append(nums[i])backtrack(i+1, path)path.pop()# returnbacktrack(0, [])return res

搜索问题：N皇后

N皇后问题简介
N皇后问题要求在一个N×N的棋盘上放置N个皇后，使得它们互不攻击。这意味着任何两个皇后都不能处于同一行、同一列或同一对角线上。

解题思路
这个问题可以通过回溯法解决，核心思想是逐行放置皇后，并在每一行中尝试所有列，直到找到一个合法的位置。我们需要一个方法来检查在放置每个新的皇后时，棋盘的状态是否仍然合法。

def solveNQueens(n):board = [["."] * n for _ in range(n)]res = []def isValid(board, row, col):for i in range(row):# 检查列是否合法if board[i][col] == 'Q':return False# 检查左上对角线if col - i - 1 >= 0 and board[row - i - 1][col - i - 1] == 'Q':return False# 检查右上对角线if col + i + 1 < n and board[row - i - 1][col + i + 1] == 'Q':return Falsereturn Truedef backtrack(board, row):if row == n:res.append(["".join(row) for row in board])returnfor col in range(n):if not isValid(board, row, col):continueboard[row][col] = "Q"backtrack(board, row + 1)board[row][col] = "."backtrack(board, 0)return res

拓展

迭代法可以避免递归，并且在实际应用中，迭代通常比递归有更好的性能，尤其是在防止栈溢出方面。

阶乘的迭代法

def factorial(n):if n == 0:return 1pre = 1for i in range(2, n+1):result = i * prepre = resultreturn result

斐波那契数列迭代法

def fib(n):if n==0:return 0if n==1:return 1pre_n_1 = 1pre_n_2 = 0for i in range(2,n+1):result = pre_n_1 + pre_n_2pre_n_2 = pre_n_1pre_n_1 = resultreturn result

青蛙跳

一只青蛙可以一次跳 1 级台阶或者一次跳 2 级台阶，例如：

跳上第 1 级台阶只有一种跳法：直接跳 1 级即可。 跳上第 2 级台阶有两种跳法：每次跳 1 级，跳两次；或者一次跳 2 级。 问要跳上第 n 级台阶有多少种跳法？

递归法

def jump(n):if n <= 2:return nreturn jump(n - 1) + jump(n - 2)

迭代法

def jump(n):if n <= 2:return npre_n_1 = 2pre_n_2 = 1for i in range(3,n+1):result = pre_n_1 + pre_n_2pre_n_2 = pre_n_1pre_n_1 = resultreturn result

参考文献

一文读懂递归算法
一文看懂什么是递归