一.题目要求
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
二.题目难度
中等
三.输入样例
示例 1:
输入:candidates = [2,3,6,7], target = 7
输出:[[2,2,3],[7]]
解释:
2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选, 7 = 7 。
仅有这两种组合。
示例 2:
输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]
示例 3:
输入: candidates = [2], target = 1
输出: []
提示:
1 <= candidates.length <= 30
2 <= candidates[i] <= 40
candidates 的所有元素 互不相同
1 <= target <= 40
四.解题思路
维护一个sum,当sum≥target时返回,若恰好等于就加入ans。
实现的时候卡在一个地方很长时间,具体见代码
五.代码实现
一开始写出来的代码是这样的:
void dfs(vector<vector<int>>& ans, vector<int>& path,vector<int> candidates, int sum, int target) {if (sum == target) {ans.push_back(path);return;}if (sum > target)return;//问题出现在这一块for (int i = 0; i < candidates.size(); i++) {path.push_back(candidates[i]);sum += candidates[i];dfs(ans, path, candidates, sum, target);sum -= candidates[i];path.pop_back();}}
};
问题出现在for循环枚举每一次递归能取的树上:若按上述代码来画递归树,会变成这个样子:
以 candidates = [2,3,6,7], target = 7 为例:
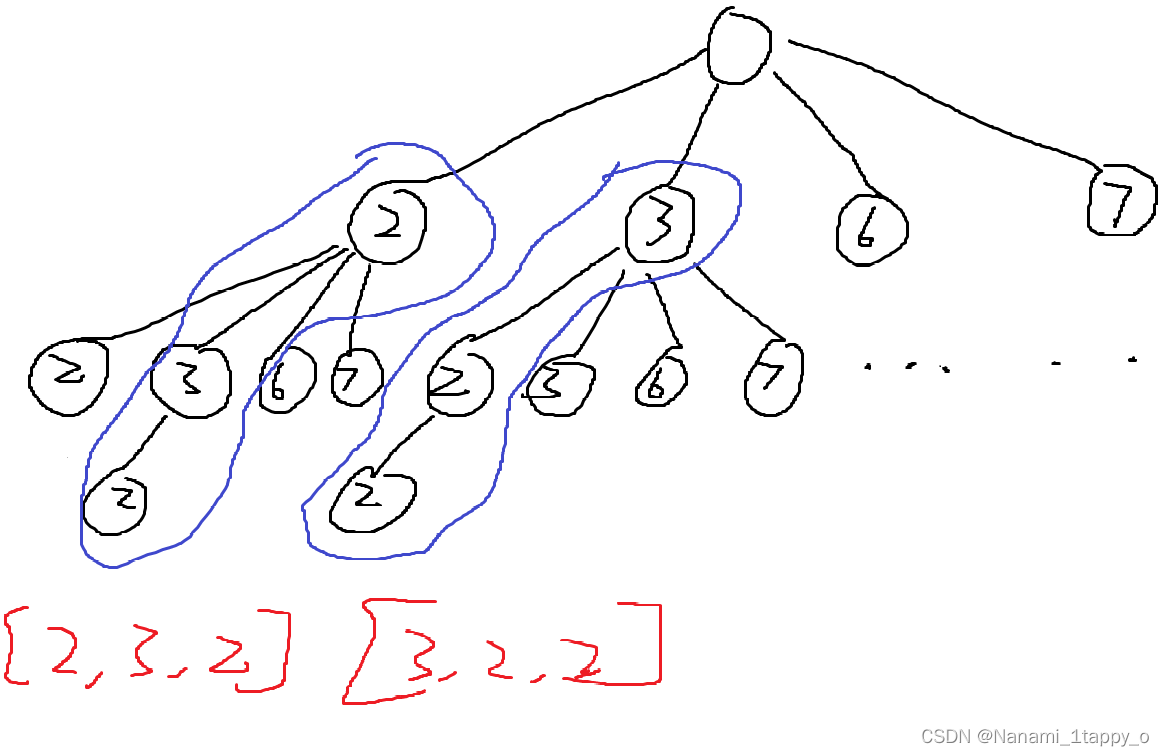
会导致有重复选择,需要每次循环把起始位置传给下一层递归,比如从3开始,那么下一次递归选数也要从3开始。
改正后:
class Solution {
public:vector<vector<int>> combinationSum(vector<int>& candidates, int target) {vector<vector<int>> ans;vector<int> path;dfs(ans, path, candidates, 0, 0, target);return ans;}void dfs(vector<vector<int>>& ans, vector<int>& path,vector<int> candidates, int sum, int start, int target) {if (sum == target) {ans.push_back(path);return;}if (sum > target)return;//设初始位置,传给下层for (int i = start; i < candidates.size(); i++) {path.push_back(candidates[i]);sum += candidates[i];dfs(ans, path, candidates, sum, i, target);sum -= candidates[i];path.pop_back();}}
};
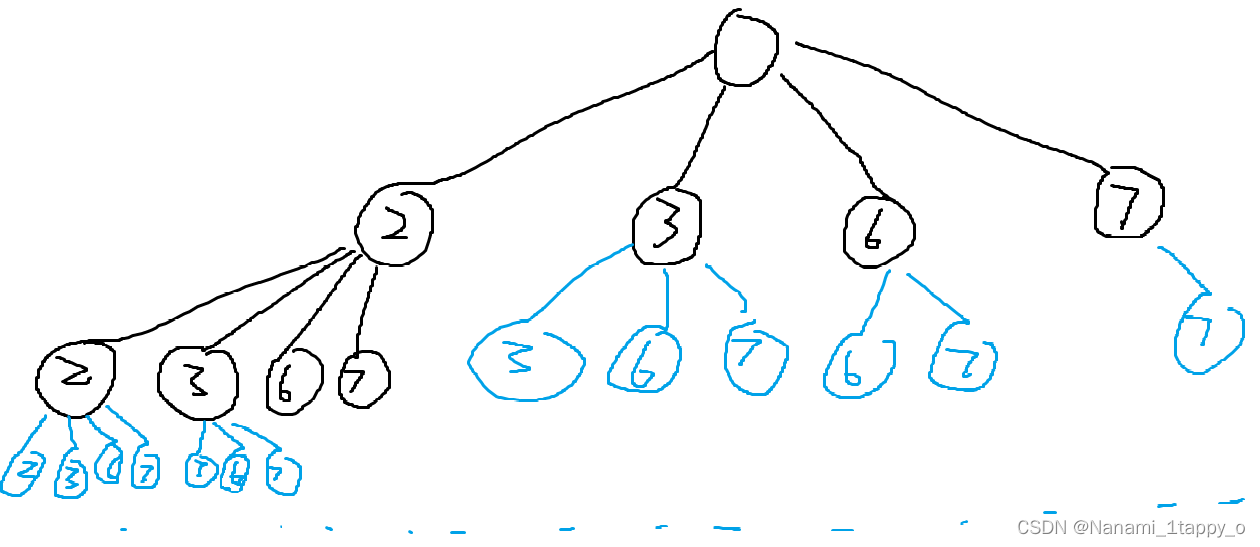
这样就是正确的树了
六.题目总结
要考虑好有顺序无顺序,有放回无放回