看这篇前请先把我上一篇了解一下:深入理解数据结构第一弹——二叉树(1)——堆-CSDN博客
前言:
相信很多学习数据结构的人,都会遇到一种情况,就是明明最一开始学习就学习了时间复杂度,但是在后期自己写的程序或者是做到哪个需要判断时间复杂度的题时,仍然判断不出来时间复杂度是多少,今天,我们结合我们上期学习的堆,给大家深入剖析一下时间复杂度这个概念,同时更深入的理解堆的概念,方便我们后期应用堆进行排序等。
目录
一、堆排序
1、堆排序的大体思路
2、堆排序的实例讲解
二、堆排序的时间复杂度
向下排序的时间复杂度
向上排序的时间复杂度
堆排序整体的时间复杂度
总结
一、堆排序
1、堆排序的大体思路
在上一篇我们已经讲过了堆是什么东西,我们已经知道堆有大堆和小堆两种形式,堆排序的想法正是借助它的这个特点诞生的,例如:
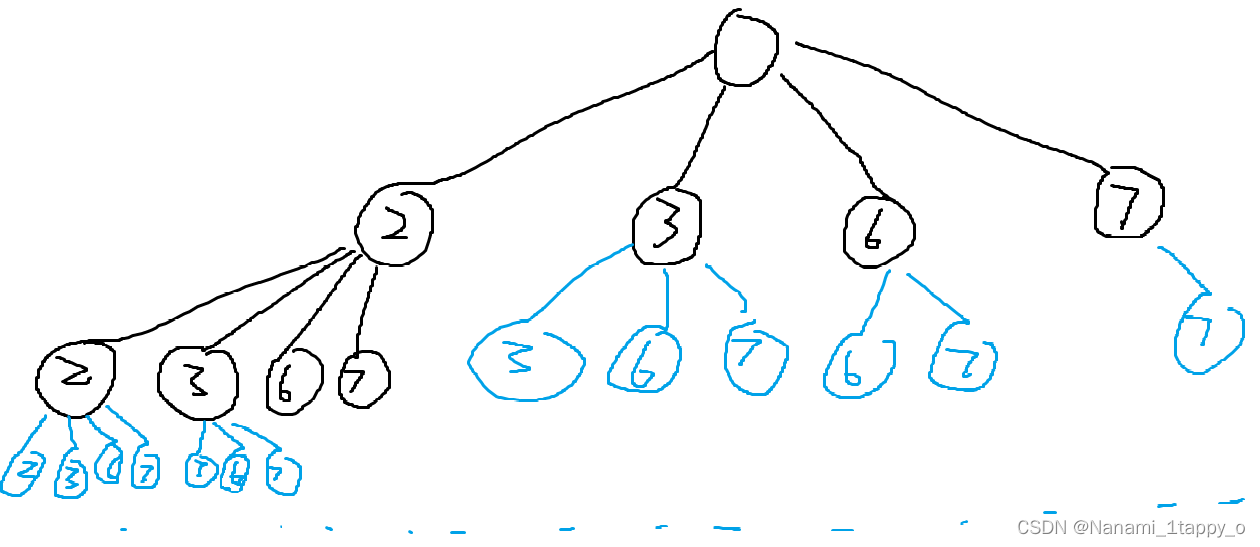
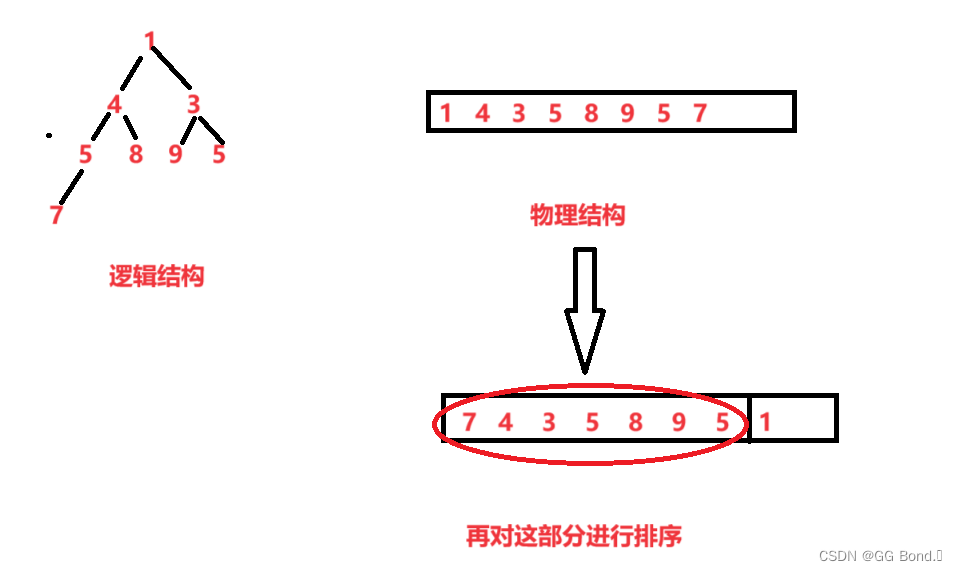
数组 { 7,8 ,3 ,5 ,1 ,9 ,5 ,4}在堆中分布为:

如图展示的是小堆,首先我们先强调一点,降序是需要小堆来解决,升序是需要大堆来解决
比如说图上这个数组,我们要求它的降序序列时,因为堆顶元素一定是堆中最小的,所以我们就可以把堆顶元素与堆尾元素进行交换,然后把堆尾元素刨除在外再进行降序排列
2、堆排序的实例讲解
堆排序与堆相比并没有什么新东西,把我前面那章看明白,这里直接把代码呈上
(除了test.c)其他的是直接从上一章搬过来的
Seqlist.h
typedef int HPDataType;
typedef struct Heap
{HPDataType* a;int sz;int capacity;
}HP;//初始化
void HeapInit(HP* php);
//销毁
void HeapDestory(HP* php);
//插入
void HeapPush(HP* php, HPDataType x);
//删除
void HeapPop(HP* php);
//找堆顶元素
HPDataType HeapTop(HP* php);
//判断是否为空
bool HeapEmpty(HP* php);
//算个数
int HeapSize(HP* php);test.c
//堆排序
void HeapSort(int* a, int n)
{//建堆——向下调整建堆O(N-log(n))for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(a, n, i);}int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);//再调整,选出次小数AdjustDown(a, end, 0);end--;}
}
int main()
{int a[] = { 7,8,3,5,1,9,5,4 };HeapSort(a, sizeof(a) / sizeof(int));return 0;
}Seqlist.c
//堆
//初始化
void HeapInit(HP* php)
{assert(php);php->a = NULL;php->capacity = 0;php->sz = 0;
}
//销毁
void HeapDestory(HP* php)
{free(php->a);free(php);
}
//交换
void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}
//删除//向上调整(小堆)
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}
//向下调整
void AdjustDown(int* a, int n, int parent)
{int child = parent * 2 + 1;while (child<n){if (child+1<n&&a[child + 1] < a[child]){++child;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}//插入
void HeapPush(HP* php, HPDataType x)
{assert(php);if (php->sz == php->capacity){int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity);php->a = tmp;php->capacity = newcapacity;}php->a[php->sz] = x;php->sz++;//向上调整AdjustUp(php->a, php->sz - 1);
}
//删除
void HeapPop(HP* php)
{assert(php);assert(!HeapEmpty(php));Swap(&php->a[0], &php->a[php->sz - 1]);php->sz--;//向下调整AdjustDown(php->a, php->sz,0);
}
//判断是否为空
bool HeapEmpty(HP* php)
{assert(php);return php->sz == 0;
}
//找堆顶元素
HPDataType HeapTop(HP* php)
{assert(php);assert(!HeapEmpty(php));return php->a[0];
}
//算个数
int HeapSize(HP* php)
{assert(php);return php->sz;
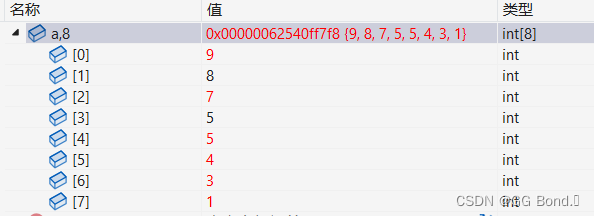
}实现上述代码,我们就可以实现堆排序了
二、堆排序的时间复杂度
我们都知道在实现堆时有向上排序和向下排序两种,细心的人可能已经注意到,我在实现上面那个堆排序用例时,用的是向下排序,原因就是向下排序的时间复杂度更低,接下来,我们就来分析一下这两种排序各自的时间复杂度
向下排序的时间复杂度
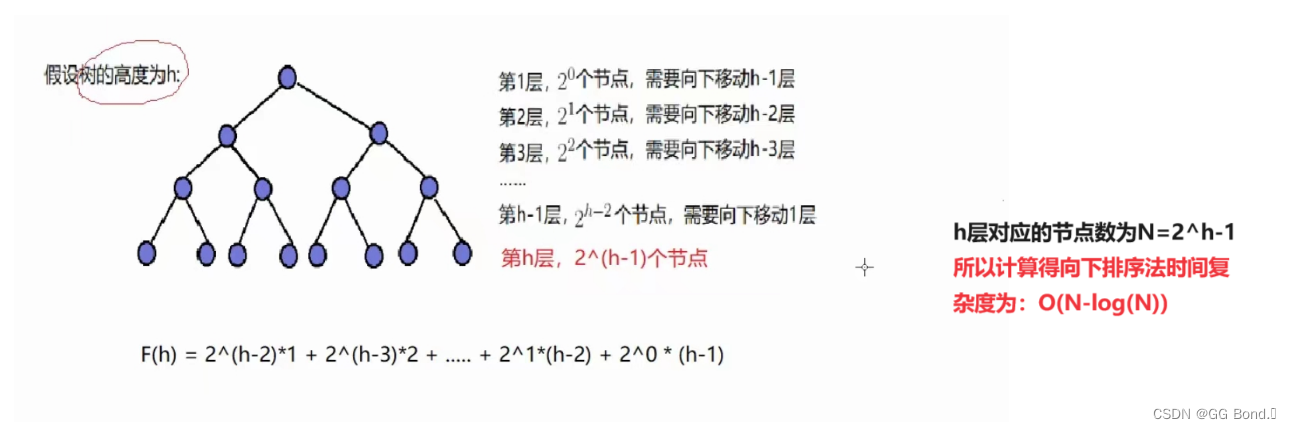
向上排序的时间复杂度
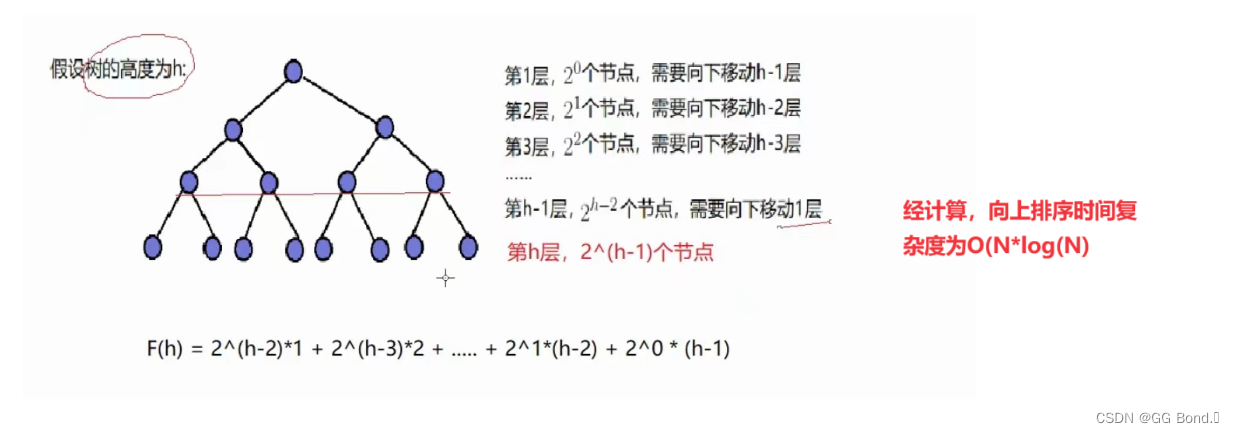
堆排序整体的时间复杂度

计算堆排序整体的时间复杂度就是计算上面这两步的时间复杂度
第一步:
因为这一步实际上就是多次向下调整建堆,所以这一步时间复杂度就是向下调整法时间复杂度的倍数,那根据渐进表示法就可以表示为O(N-log(N)),因为当N很大时,log(N)比N小很多,所以可以忽略表示为O(N)
第二步:
第二步外循环需要N次,内循环看似每次都是一个完整的向下排序法,但其实随着循环次数的增加,里面向下排序的时间复杂度在不断减小,因为堆尾排过去的数字实际上就不用再参与堆排序的,所以这一步时间复杂度实际上是O(N*log)
因此,堆排序的时间复杂度为O(N+N*log(N))
总结
堆排序及其时间复杂度的讲解就到此为止了,如果有不理解的地方欢迎在评论区中指出或者与我私信交流,欢迎各位大佬来访!!!
创作不易,还请各位大佬点赞支持!!!