逻辑回归(Logistic Regression)是一种常用的统计学习方法,用于解决二分类问题。虽然名字中包含“回归”,但逻辑回归实际上是一种分类算法,而不是回归算法。它的基本原理是使用逻辑函数(也称为Sigmoid函数)将输入的线性组合映射到0和1之间,从而得到一个概率值,表示样本属于某一类的概率。下面是逻辑回归的详细解释:
1. 基本原理:
逻辑回归的基本思想是将输入特征的线性组合通过一个sigmoid函数映射到[0,1]之间,表示样本属于某一类的概率。其数学表达式为:
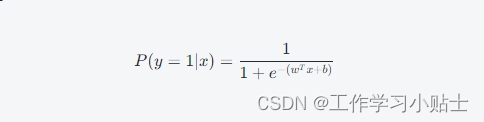
其中,P(y=1∣x) 表示在给定输入特征 x 的情况下,样本属于类别1的概率; 是特征的权重向量;b 是偏置项;
是自然对数的底。
2. 损失函数:
逻辑回归使用对数似然损失函数来衡量模型预测结果与真实标签之间的差异。对于二分类问题,损失函数定义如下:

其中,m 是样本数量,是第 i 个样本的真实标签,
是模型预测的标签。
3. 参数优化:
逻辑回归通常使用梯度下降(Gradient Descent)等优化算法来最小化损失函数,更新参数 �w 和 �b 以使损失函数达到最小值。
4. 决策边界:
通过学习到的参数 和 b,可以得到一个决策边界,用于将样本分为两个类别。
5. 正则化:
为了防止模型过拟合,逻辑回归可以使用 L1 正则化或 L2 正则化。正则化项会加到损失函数中,以惩罚模型的复杂度。
6. 多类别分类:
逻辑回归也可以扩展到多类别分类问题,其中常用的方法是一对多(One-vs-Rest)或一对一(One-vs-One)策略。
总之,逻辑回归是一种简单而有效的分类算法,在实际应用中被广泛使用。虽然它的名字中带有“回归”,但它实际上是一种分类模型。