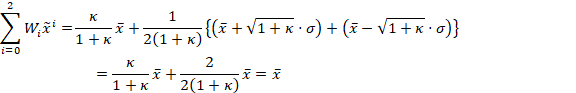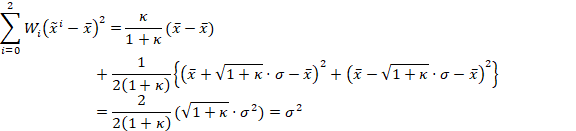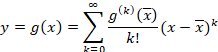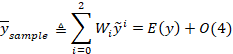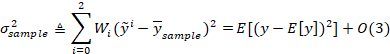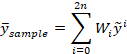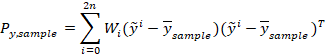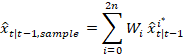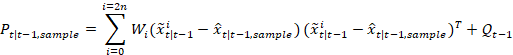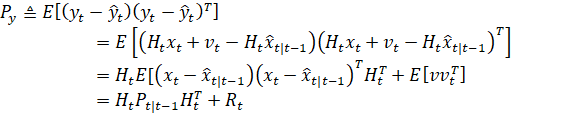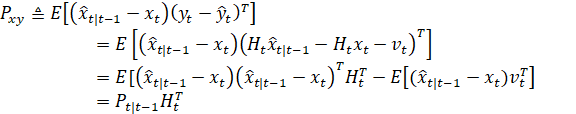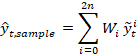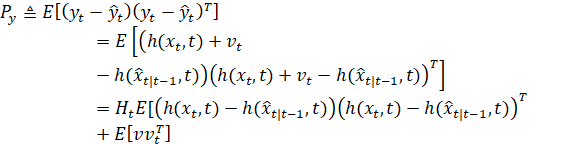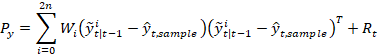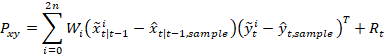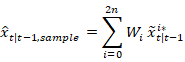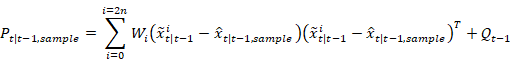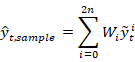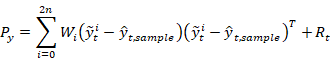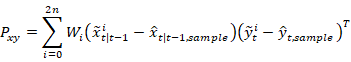pdf和图片链接:
链接:https://pan.baidu.com/s/1q8tIy1q5gqlhYEKH1l8frg
提取码:yyds1.1概述
无迹卡尔曼滤波(Unscented Kalman Filter),最初由Julier和Uhlmann提出,使用了一种不同的方法来计算误差协方差矩阵。它不使用(连续时间)黎卡提方程(Riccati Equations,形如、
的一类非线性方程)或(离散时间)协方差传播和更新规律。关键的思想是基于一组特殊的样本点来估计误差协方差,这些点被称为
点(Sigma Points),这些点直接通过原始非线性模型传播。
1.2 无迹变换
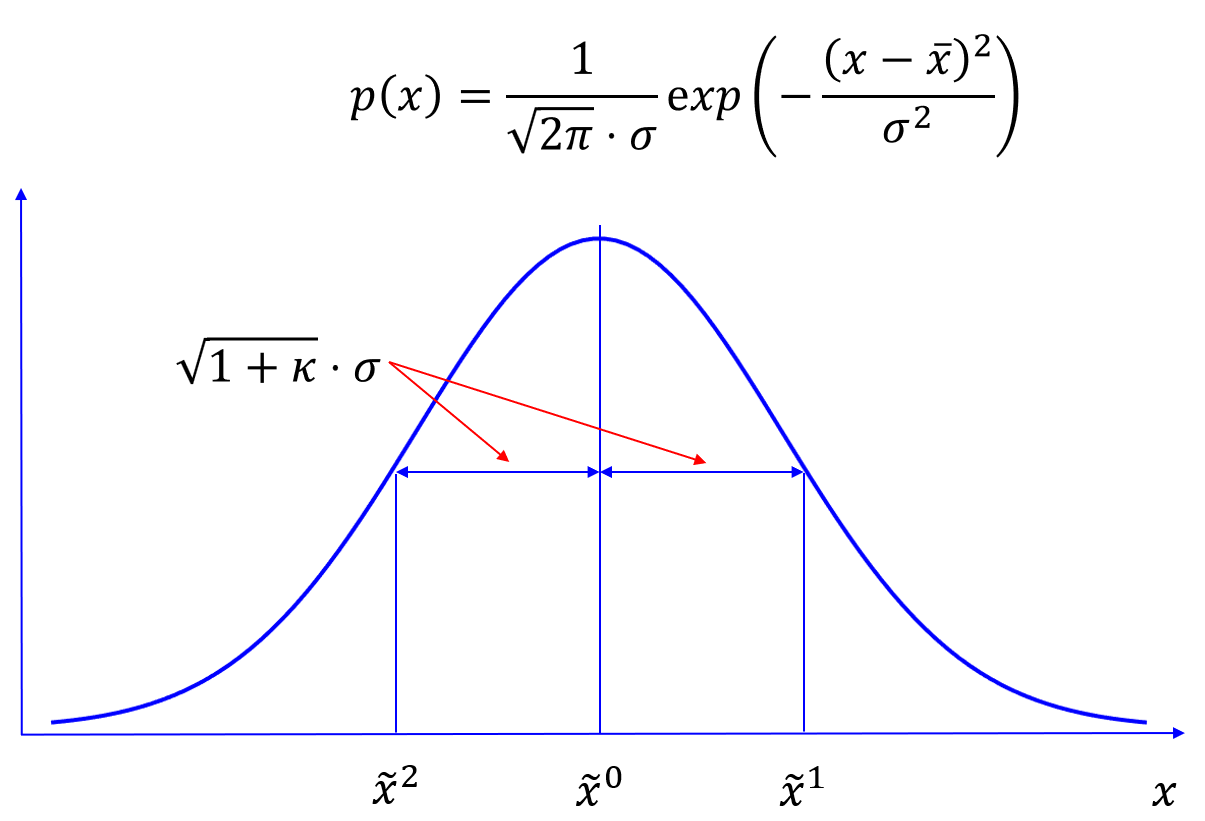
以一维高斯分布为例,随机变量为X,其中高斯分布的数学表达式为:
其中均值为
,方差为
,其分布函数如图1所示:
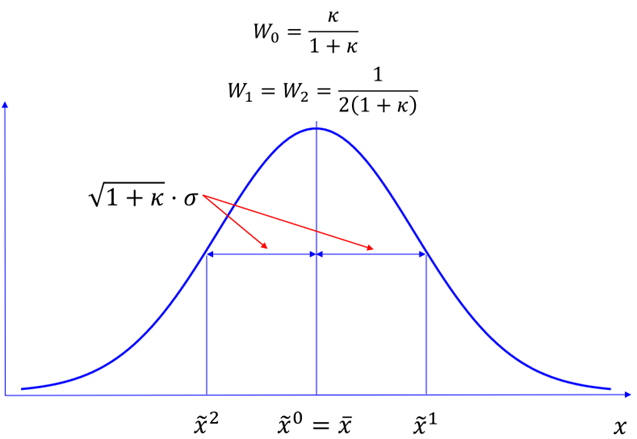
无迹变换表示有三个特殊样本点的高斯分布,称为
点,三个点分别为:
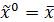
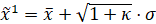
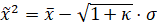
其中,
是需要调整的
点的参数,
是用于计算均值和方差的第
个
点的权值。
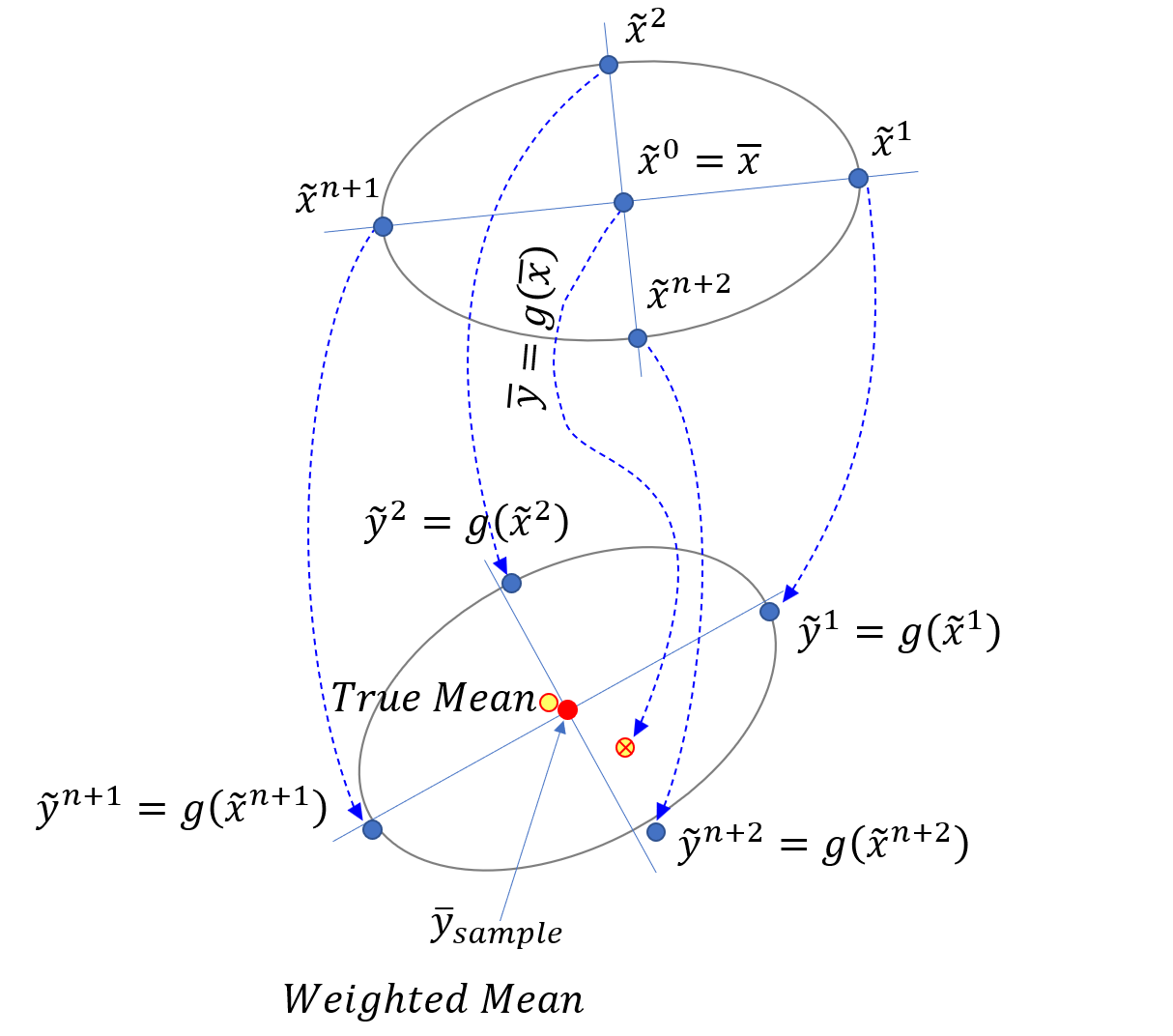
通过计算三个
点的加权均值,得出三个
点的加权均值与高斯分布的真实均值一致:
通过计算三个
点的加权方差,三个
点的加权方差与方差的真实值一致:
因此,
点的均值和方差提供了任意参数
值的真实高斯分布的正确均值和方差。
如图所示,现在有一个从x到y的非线性变换:
其中函数
是解析函数。
y的分布不再是高斯分布,但其均值
和方差
可以表征该分布。
我们可以证明通过非线性函数变换后的加权均值可以逼近三阶的真实均值。
其中
是一个4阶以上的小量。
进一步,我们可以证明加权方差可以近似真实方差到二阶。
1.3例子
如图所示,有
的分段线函数(为了可微性,两条线用光滑曲线连接)。
x的均值变换为
,这并不是y分布的真实均值,通过检验我们可以看到:
点的加权平均值可以给出较好的平均值:
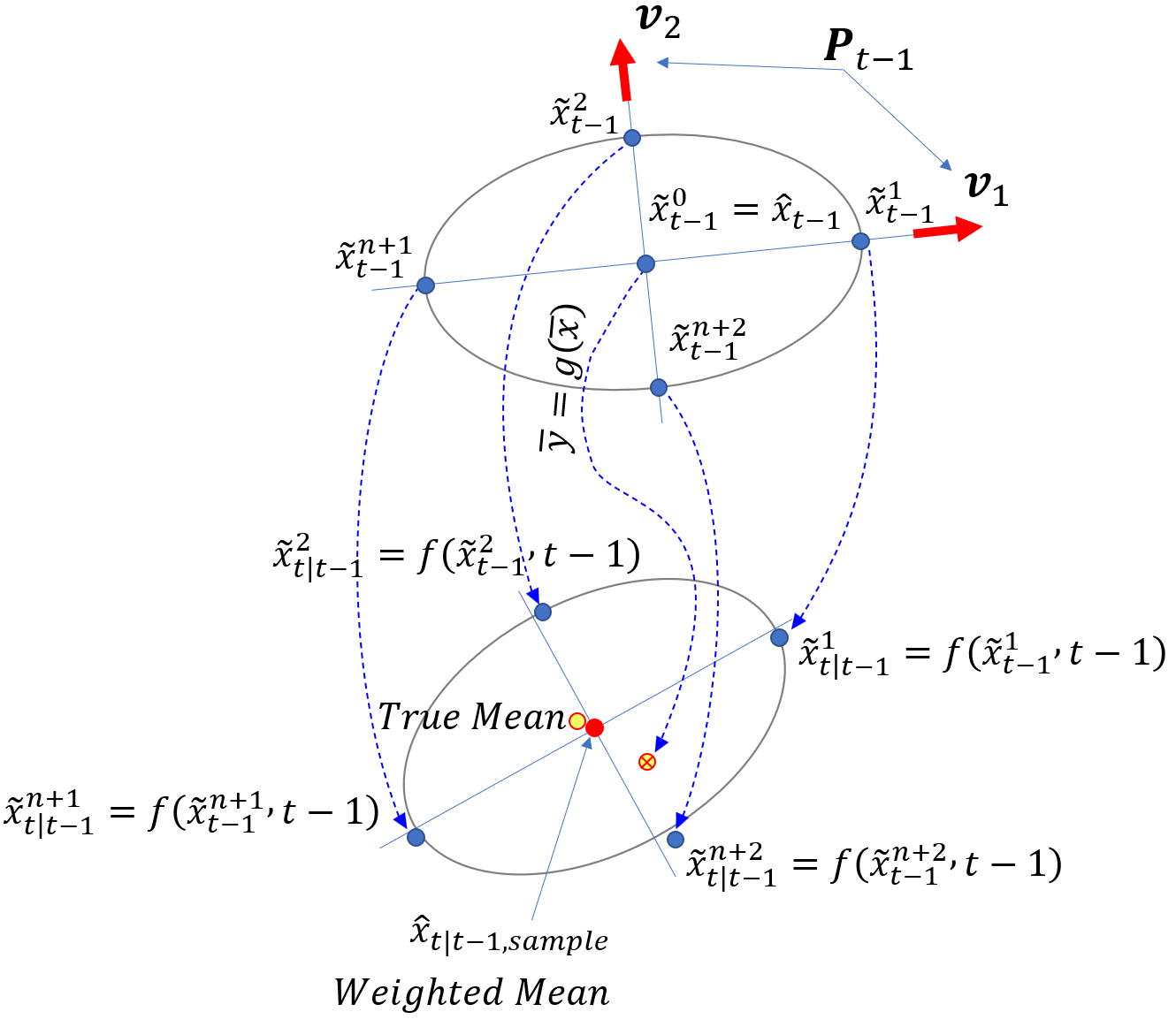
1.4 多元高斯分布的
点
1) 一般来说,对于n维高斯分布,我们使用2n+1个
点。
注意协方差矩阵
是实数、对称和正定的。因此,它可以对角化。
其中
2)
点沿单位长度的单个特征向量取
.
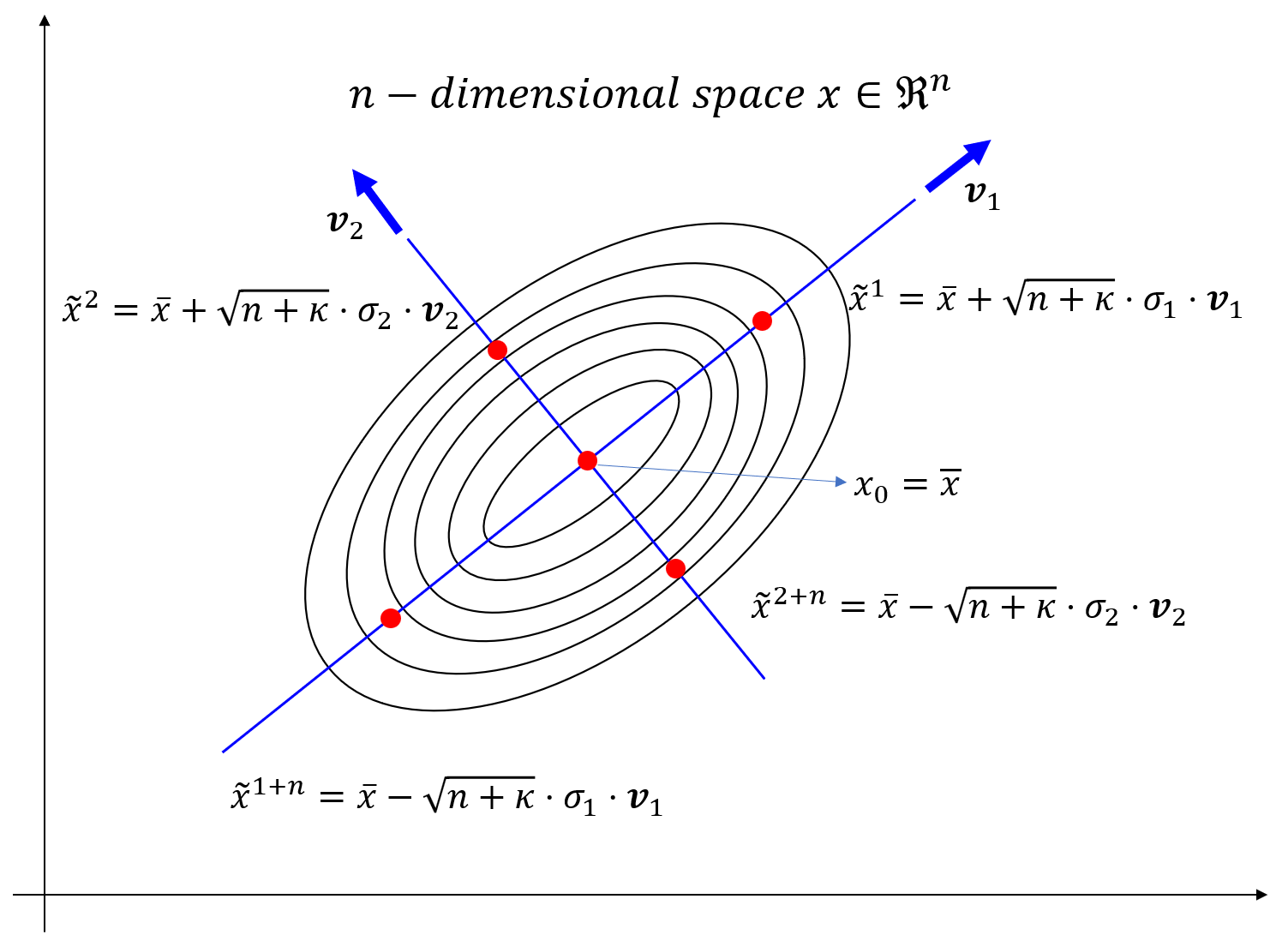


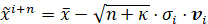
3) 和以前一样,所有的
点通过一个非线性解析函数传播,
,属于多元函数。
4) 对于这些传播点,计算加权平均值:
加权协方差为:
我们可以证明加权均值可以近似三阶真实均值,加权协方差可以近似二阶真实均值。这种采样方法称为无迹变换。
1.5无迹卡尔曼滤波
考虑一个非线性离散时间动态系统:
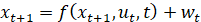
在不丢失一般性的情况下,我们将u设置为零,
。
过程噪声和测量噪声是零均值、不相关(白)噪声,协方差为
和
。

在时刻t-1,后验估计
和后验误差协方差是可用的:
问题是使用无迹变换找到递归公式:
1)状态和协方差的传播:从
和
中求
和
;
2)状态和协方差的更新:从
和
中找到
和
。
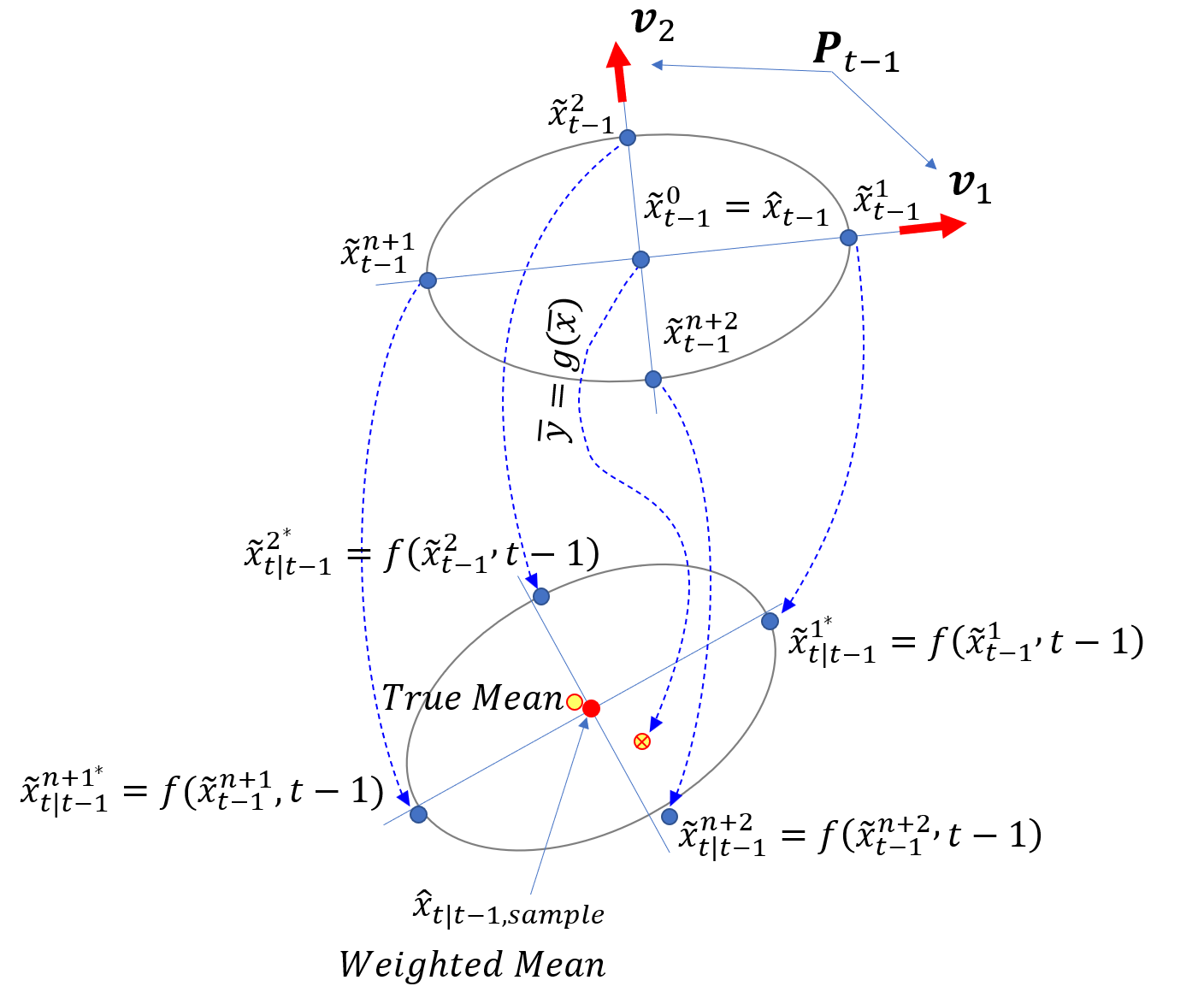
1.6 状态传播
1) 找到协方差
的特征值和特征向量,生成2n+1个点;
2) 通过状态方程传播
点,注意过程噪声为零均值:
3) 对于这些2n+1个
点,计算加权平均值:
1.7 协方差传播
先验协方差计算为:
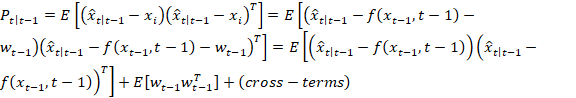
是未知的因为我们不知道
的确切状态。但是,加权平均值
近似于三阶。因此,我们将
替换为加权均值,并使用2n+1个
点计算先验协方差。
注意,预测的协方差在二阶前是正确的。为简便起见,下标“sample”将在下文中省略。
1.8利用新的协方差获得卡尔曼增益
我们的目标是使用
点更新状态和协方差。然而,标准卡尔曼增益和协方差更新法不适用于无迹变换。相反,我们将考虑一种新的替代方法。卡尔曼增益为
,但
矩阵对我们的非线性系统是不可用的。相反,我们使用下面的公式,
对于一个线性时变系统,这个新公式可以用结构证明。
结合上述两点,证明了卡尔曼增益的新公式。输出y的协方差称为“创新协方差”。
1.9 状态更新
通过对先验协方差
应用无迹变换可以更新状态和协方差。
1) 通过检验通过测量方程产生的输出,并通过分布来获得新协方差;
2) 计算先验协方差的特征值和特征向量:
3) 然后生成2n+1个
点,并估计输出y的分布与
点的均值和协方差;
4) 利用测量函数的确定性部分,将
点映射到:
5)
点的加权均值:
6) 结合创新协方差得到:
7) 用
点计算第一项:
同理,交叉协方差由:
8) 卡尔曼增益是
。
9) 状态更新为:
1.10协方差更新
1) 协方差更新公式中包含测量矩阵
,需要替换。
我们可以使用创新协方差:
2) 协方差更新公式中插入协方差更新公式中插入
:
式中,利用卡尔曼增益
消去测量矩阵
。
3) 利用
点,可以这样计算:
1.11无迹卡尔曼滤波器的递归算法
1) 给定
和
,通过计算
的特征值和向量对
点进行抽样;
2) 将
点通过非线性模型传播得到
;
3) 用2n+1个
点计算均值和方差:
4) 对
再次采样2n+1个
点;
5) 根据非线性测量方程,将传播的
点变换为输出估计
,并计算输出估计:
6) 利用2n+1个点的传播输出估计来评估创新协方差和交叉协方差,得到卡尔曼增益:
7) 用卡尔曼增益更新状态估计:
8) 更新后验协方差:
9) 设
,重复上述过程。
不需要雅可比矩阵,不需要偏导。用标准差点估计协方差比用雅可比矩阵估计协方差更精确。
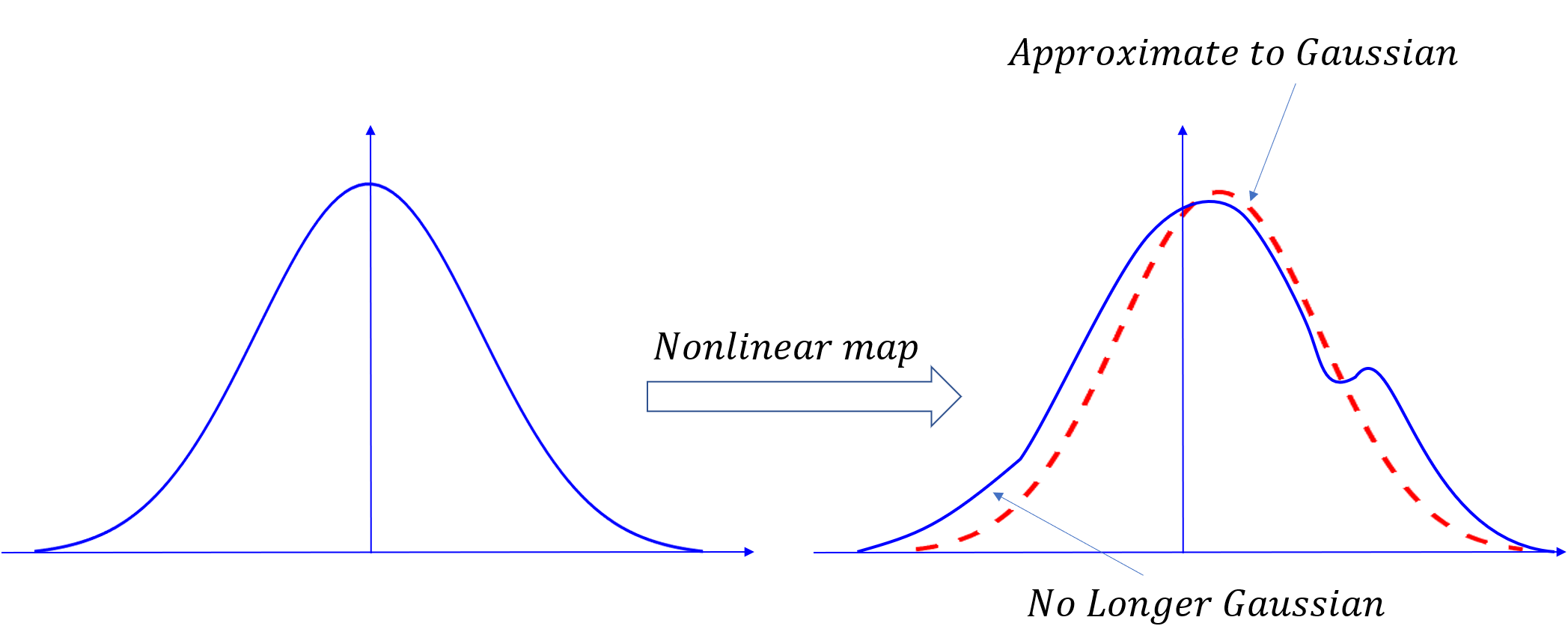
警告!随机变量通过非线性方程
,
变换后的分布不再是高斯分布,虽然原来的分布是高斯分布。
无迹卡尔曼滤波器将此分布近似为高斯分布,并以均值和协方差为特征。虽然该近似值精确到2阶,但随着过程的重复,与完全高斯分布的差异可能会增大。
无迹卡尔曼滤波(UKF)推导
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.hqwc.cn/news/588539.html
如若内容造成侵权/违法违规/事实不符,请联系编程知识网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
玩机进阶教程-----高通9008线刷XML脚本修改备份 檫除的操作步骤解析
在高通9008官方固件中我们可以看到刷写需要的脚本rawprogram0.xml和辅助脚本patch0.xml,脚本的作用在于将固件内各个分区对应写入手机内。根据分区地址段。然后判断脚本中那些分区不写入。以下步骤将分析emmc字库为例来讲解如何将默认刷入脚本修改为备份 檫除脚本。…
IpcRenderer.invoke Error: An object could not be cloned.
这个错误信息提示“Uncaught (in promise) Error: An object could not be cloned.”通常发生在使用 Electron 的 IPC 通信过程中,尝试通过 ipcRenderer.invoke 或 ipcMain.handle 发送不能被克隆的对象时。JavaScript 中一些特殊对象或包含循环引用的对象无法通过 …
【教学类-09-07】20240401细线迷宫图02+箭头图片(A4横版一页-2份竖版)
作品展示 作品展示 word模板 重点说明 代码展示 批量制作细线条的迷宫图(A4横板一面2张竖版)箭头图片
作者:
1、落难Coder https://blog.csdn.net/u014297502/article/details/124839912
2、AI对话大师
3、阿夏
作者:2024年4月3日
numint(input(几人&…
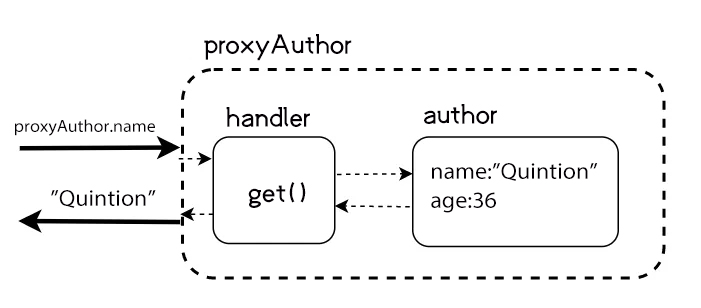
JavaScript 对象管家 Proxy
JavaScript 在 ES6 中,引入了一个新的对象类型 Proxy,它可以用来代理另一个对象,并可以在代理过程中拦截、覆盖和定制对象的操作。Proxy 对象封装另一个对象并充当中间人,其提供了一个捕捉器函数,可以在代理对象上拦截…
36.基于SpringBoot + Vue实现的前后端分离-高校汉服租赁网站系统(项目 + 论文)
项目介绍 本站是一个B/S模式系统,采用SpringBoot Vue框架,MYSQL数据库设计开发,充分保证系统的稳定性。系统具有界面清晰、操作简单,功能齐全的特点,使得基于SpringBoot Vue技术的高校汉服租赁网站系统设计与实现管理…
基于java+springboot+vue实现的医院门诊在线挂号系统(文末源码+Lw)23-222
摘 要
伴随着信息技术与互联网技术的不断发展,校园也进到了一个新的信息化时代,传统管理技术性没法高效率、容易地管理医院门诊在线挂号信息内容。为了实现时代的发展必须,提升医院门诊在线挂号高效率,各种各样医院门诊在线挂号…
高效学习方法:冥想背诵,看一句念一句,再每个词分析位置及语法等合理性,忘记哪个词再看猜下为什么会忘,跟自己的表达哪里不一样。
原则:易学则易行,则效果最好。《易经》
你提到的这种学习方法结合了多种记忆和理解技巧,可以帮助提高学习效率。下面是对这种方法的一个详细解释和一些建议: 冥想背诵:通过冥想来集中注意力,可以帮助你在没…
AI智能校色解决方案,专业级画质提升
由于拍摄环境、设备性能以及编辑经验等多种因素的影响,视频画质往往难以达到理想状态。这时,一款高效、智能的校色解决方案就显得尤为重要。美摄科技凭借深厚的图像处理技术和AI算法研发实力,推出了全新的AI智能校色解决方案,助力…
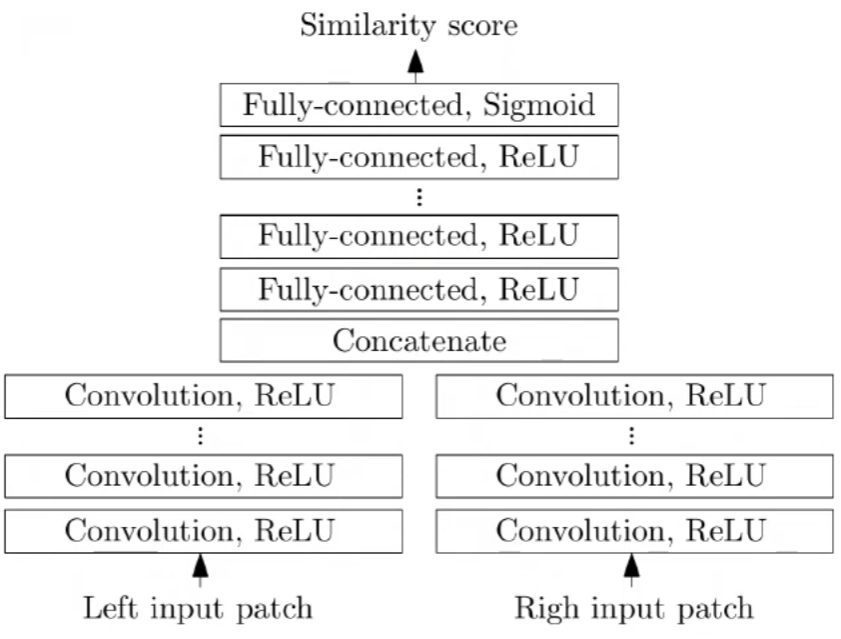
SAD法(附python实现)和Siamese神经网络计算图像的视差图
1 视差图
视差图:以左视图视差图为例,在像素位置p的视差值等于该像素在右图上的匹配点的列坐标减去其在左图上的列坐标
视差图和深度图: z f b d z \frac{fb}{d} zdfb 其中 d d d 是视差, f f f 是焦距, b b…
C语言第三十九弹---预处理(上)
✨个人主页: 熬夜学编程的小林
💗系列专栏: 【C语言详解】 【数据结构详解】
预处理
1、预定义符号
2、#define定义常量
3、#define定义宏
4、带有副作用的宏参数
5、宏替换的规则
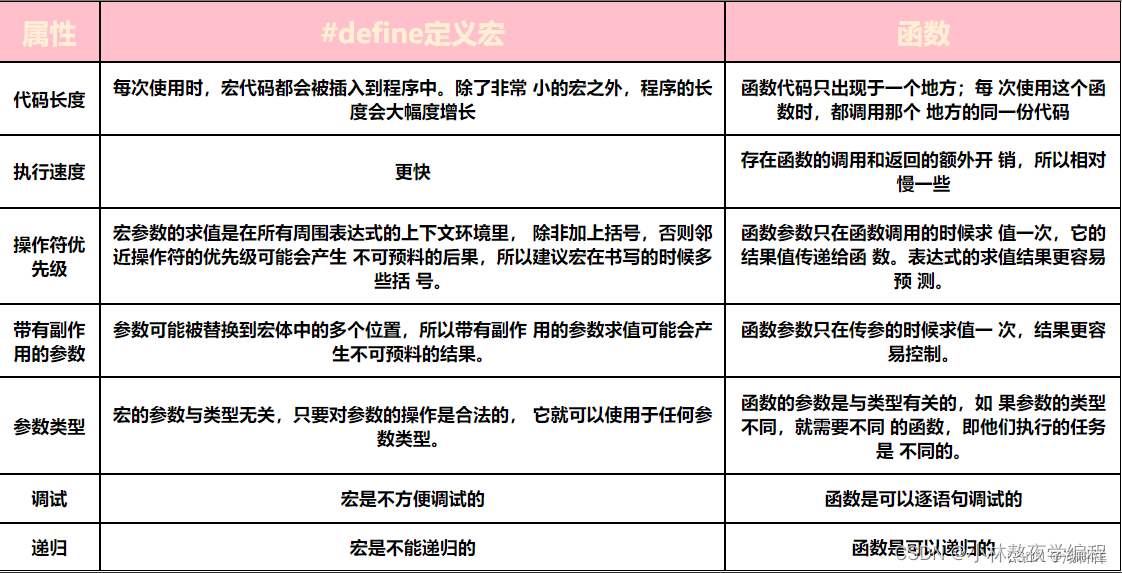
6、宏和函数的对比
总结 在C语言中,预处…
臻奶惠无人售货机:新零售时代的便捷消费革命
臻奶惠无人售货机:新零售时代的便捷消费革命
在新零售的浪潮中,智能无人售货机作为一个创新的消费模式,已经成为距离消费者最近的便捷购物点之一。这种模式不仅能够满足居民对消费升级的需求,还能通过建立多样化和多层次的消费体…
【御控物联】JavaScript JSON结构转换(12):对象To数组——键值互换属性重组
文章目录 一、JSON结构转换是什么?二、核心构件之转换映射三、案例之《JSON对象 To JSON数组》四、代码实现五、在线转换工具六、技术资料 一、JSON结构转换是什么?
JSON结构转换指的是将一个JSON对象或JSON数组按照一定规则进行重组、筛选、映射或转换…