算法基础--递推-编程知识

算法基础--递推

😀前言
递推算法在计算机科学中扮演着重要的角色。通过递推，我们可以根据已知的初始条件，通过一定的规则推导出后续的结果，从而解决各种实际问题。本文将介绍递推算法的基础知识，并通过一些入门例题来帮助读者更好地理解和掌握递推算法的应用。

🏠个人主页：尘觉主页

文章目录

算法基础
- 递推
- - 入门例题
  - - 斐波那契数列
    - 费解的开关
- 😄总结

算法基础

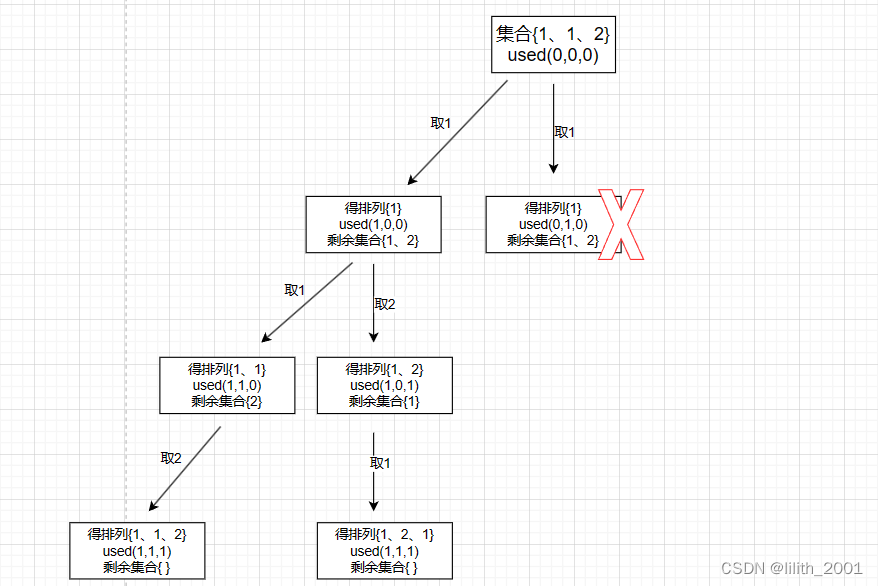
递推

入门例题

斐波那契数列

输入一个整数 n ，求斐波那契数列的第 n 项。

假定从 0 开始，第 0 项为 0。

数据范围
0≤n≤39
样例
输入整数 n=5

返回 5

题解

该题十分基础，我们要理解斐波那契数列的组成，数列中从每一项都是前两项的和，所以如果不要求存下一些数的数值，我们就可以直接使用，几个变量操作不用进行数组创建。

class Solution {
public:int Fibonacci(int n) {if(n<=1)return n;if(n==2) return 1;int a=1,b=1;int t;for(int i=3;i<=n;i++){t=a+b;a=b;b=t;}return t;}
};

费解的开关

你玩过“拉灯”游戏吗？

25 盏灯排成一个 5×5 的方形。

每一个灯都有一个开关，游戏者可以改变它的状态。

每一步，游戏者可以改变某一个灯的状态。

游戏者改变一个灯的状态会产生连锁反应：和这个灯上下左右相邻的灯也要相应地改变其状态。

我们用数字 1 表示一盏开着的灯，用数字 0 表示关着的灯。

下面这种状态

10111
01101
10111
10000
11011
在改变了最左上角的灯的状态后将变成：

01111
11101
10111
10000
11011
再改变它正中间的灯后状态将变成：

01111
11001
11001
10100
11011
给定一些游戏的初始状态，编写程序判断游戏者是否可能在 6 步以内使所有的灯都变亮。

输入格式
第一行输入正整数 n，代表数据中共有 n 个待解决的游戏初始状态。

以下若干行数据分为 n 组，每组数据有 5 行，每行 5 个字符。

每组数据描述了一个游戏的初始状态。

各组数据间用一个空行分隔。

输出格式
一共输出 n 行数据，每行有一个小于等于 6 的整数，它表示对于输入数据中对应的游戏状态最少需要几步才能使所有灯变亮。

对于某一个游戏初始状态，若 6 步以内无法使所有灯变亮，则输出 −1。

数据范围
0<n≤500
输入样例：
3
00111
01011
10001
11010
11100

11101
11101
11110
11111
11111

01111
11111
11111
11111
11111
输出样例：

3
2
-1

题解

该题我们分析可以发现，我们可以通过枚举第一行的5个灯的32中开与不开的状态来实现，因为第一行开关确定以后，第一行的开关亮与不亮只与下一层开关有关，如果i-1行j列是关的，我们就开一下i行j列的灯就可以使上一个灯泡开，一次递推我们就可以实现是否所有灯都能开，要注意的是我们要保存一下开始的灯泡状态，因为要枚举32次，积累一下位运算>>

我们可以通过op>>i&1表示第一行的灯是否开，这是通过二进制存储实现的，我们用0表示不开，用1表示开。

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>using namespace std;
const int N=510;
char g[6][6],backup[6][6];
int dx[6]={-1,0,1,0,0},dy[6]={0,1,0,-1,0};
int n;
void turn(int x,int y){for(int i=0;i<5;i++){int a=x+dx[i],b=y+dy[i];if(a<0||a>=5||b<0||b>=5)continue;g[a][b]^=1;}
}
int main(){cin>>n;while(n--){for(int i=0;i<5;i++)cin>>g[i];int ans=10;for(int op=0;op<32;op++){memcpy(backup,g,sizeof g);int stmp=0;for(int i=0;i<5;i++){if(op>>i&1){turn(0,i);stmp++;}}for(int i=1;i<5;i++){for(int j=0;j<5;j++){if(g[i-1][j]=='0'){turn(i,j);stmp++;}}}bool suf=true;for(int j=0;j<5;j++){if(g[4][j]=='0'){suf=false;break;}}if(suf){ans=min(ans,stmp);}memcpy(g,backup,sizeof backup);}if(ans>6){cout<<-1<<endl;}else{cout<<ans<<endl;}}return 0;
}