拓扑排序--有向无环图中一个节点的所有祖先-编程知识

拓扑排序--有向无环图中一个节点的所有祖先

题目描述

给你一个正整数 n ，它表示一个 有向无环图 中节点的数目，节点编号为 0 到 n - 1 （包括两者）。

给你一个二维整数数组 edges ，其中 edges[i] = [fromi, toi] 表示图中一条从 fromi 到 toi 的单向边。

请你返回一个数组 answer，其中 answer[i]是第 i 个节点的所有祖先，这些祖先节点升序排序。

如果 u 通过一系列边，能够到达 v ，那么我们称节点 u 是节点 v 的祖先节点。

示例 1：

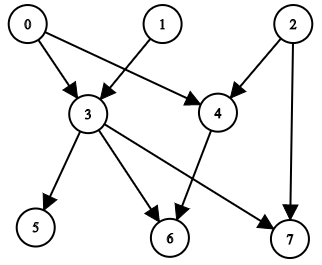
输入：n = 8, edgeList = [[0,3],[0,4],[1,3],[2,4],[2,7],[3,5],[3,6],[3,7],[4,6]]
输出：[[],[],[],[0,1],[0,2],[0,1,3],[0,1,2,3,4],[0,1,2,3]]
解释：
上图为输入所对应的图。
- 节点 0 ，1 和 2 没有任何祖先。
- 节点 3 有 2 个祖先 0 和 1 。
- 节点 4 有 2 个祖先 0 和 2 。
- 节点 5 有 3 个祖先 0 ，1 和 3 。
- 节点 6 有 5 个祖先 0 ，1 ，2 ，3 和 4 。
- 节点 7 有 4 个祖先 0 ，1 ，2 和 3 。

示例 2：

输入：n = 5, edgeList = [[0,1],[0,2],[0,3],[0,4],[1,2],[1,3],[1,4],[2,3],[2,4],[3,4]]
输出：[[],[0],[0,1],[0,1,2],[0,1,2,3]]
解释：
上图为输入所对应的图。
- 节点 0 没有任何祖先。
- 节点 1 有 1 个祖先 0 。
- 节点 2 有 2 个祖先 0 和 1 。
- 节点 3 有 3 个祖先 0 ，1 和 2 。
- 节点 4 有 4 个祖先 0 ，1 ，2 和 3 。

提示：

1 <= n <= 1000
0 <= edges.length <= min(2000, n * (n - 1) / 2)
edges[i].length == 2
0 <= fromi, toi <= n - 1
fromi != toi
图中不会有重边。
图是有向且无环的。

1. 思路

有向无环图中，每个节点的所有祖先节点集合即为该节点所有父节点（即有一条直接指向该节点的有向边的节点）的本身及其祖先节点组成集合的并集。

如果我们按照拓扑排序的顺序来遍历每个节点并计算祖先节点集合，那么遍历到某个节点时，其所有父节点的祖先节点集合都已计算完成，我们就可以直接对这些集合加上父节点本身取并集得到该节点的所有祖先节点。这一「取并集」的过程等价于在拓扑排序的过程中用每个节点的祖先集合更新每个节点所有子节点的祖先集合。

具体地，我们用哈希表数组 anc 来表示每个节点的祖先节点集合，用 e 以邻接表形式存储每个节点的所有出边，并用数组 indeg 来计算每个结点的入度。

我们可以用广度优先搜索的方法求解拓扑排序。首先我们遍历 edges 数组预处理邻接表 e 和入度表 indeg，并将所有入度为 0 的节点加入广度优先搜索队列 q。此时队列里的元素对应的祖先节点集合均为空集，且都已经更新完成。

在遍历到节点 u 时，我们首先遍历所有通过出边相邻的子节点 v，此时根据定义 u 一定是 v 的父节点，且根据拓扑序，u 的祖先节点集合 anc[u] 已经更新完毕。因此我们将 anc[u] 的所有元素和 u 加入至 anc[v] 中，并将 v 的入度 indeg[v] 减去 1。此时，如果 indeg[v]=0，则说明 anc[v] 已经更新完成，此时我们将 v 加入队列。

最终，我们需要利用嵌套数组 res 将 anc 中的每个哈希集合对应地转化为升序排序后的数组，此时 res 即为待求的升序排序的每个节点的所有祖先。我们返回 res作为答案即可。

2. 代码

public List<List<Integer>> getAncestors(int n, int[][] edges) {Set<Integer>[] anc = new Set[n];   // 存储每个节点祖先的辅助数组for (int i = 0; i < n; ++i) {anc[i] = new HashSet<Integer>();}List<Integer>[] e = new List[n];   // 邻接表for (int i = 0; i < n; ++i) {e[i] = new ArrayList<Integer>();}int[] indeg = new int[n];   // 入度表// 预处理for (int[] edge : edges) {e[edge[0]].add(edge[1]);++indeg[edge[1]];}// 广度优先搜索求解拓扑排序Queue<Integer> q = new ArrayDeque<Integer>();for (int i = 0; i < n; ++i) {if (indeg[i] == 0) {q.offer(i);}}while (!q.isEmpty()) {int u = q.poll();for (int v : e[u]) {// 更新子节点的祖先哈希表anc[v].add(u);for (int i : anc[u]) {anc[v].add(i);}--indeg[v];if (indeg[v] == 0) {q.offer(v);}}}// 转化为答案数组List<List<Integer>> res = new ArrayList<List<Integer>>();for (int i = 0; i < n; ++i) {res.add(new ArrayList<Integer>());for (int j : anc[i]) {res.get(i).add(j);}Collections.sort(res.get(i));}return res;}