一、按摩师
1、题目解析

简而言之就是,找到一个按摩师的预约总是长的最长方案,还有一个限制条件,选取的预约两两不相邻。
2、算法原理
a状态表示方程
小技巧:经验+题目要求
dp[i]表示以这个节点为结尾,最长的预约时长
b状态转移方程
1、找到最近的一个节点,划分问题
2、预约节点两两不相邻
dp[i]的值如何得出呢——找到前两个节点进行对比一下,取最大值再加上我这个值
最近的节点dp[i-1]不可考虑,因为相邻了


dp[i]=min(dp[i-2],dp[i-3])+nums[i]
有些同学就开始纠结了,为啥不考虑i-4的情况呢————因为i-2包括了
c初始化
根据上面的推断,可能会遇到边界问题的节点为0,1,2 。
所以我们可以给这三个节点进行初始化。
也可以通过虚拟节点的方法进行解决
虚拟节点注意事项:
- 初始化取值需要保证后续填表值的正确性
- 注意下标映射关系
我们选择的初始化取值为0,这样不会影响到后续取值,并且向nums取值时应该i-3
以下图为例
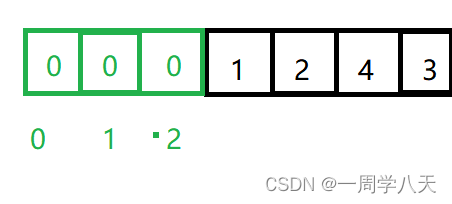
d填表顺序
从左到右
e返回值
dp表的最后两个节点的较大值
max(dp[n+2],dp[n+1])
3、代码
class Solution {
public:int massage(vector<int>& nums) {int n=nums.size();vector<int> dp(n+3,0);for(int i=3;i<n+3;i++)dp[i]=max(dp[i-2],dp[i-3])+nums[i-3];return max(dp[n+2],dp[n+1]);}
};4、解法2
算法原理
a状态表示方程
dp[i]表示以i为终点时的最大值
但是这个节点有两种情况:
f[i]表示以i为终点并且选了i节点值时的最大值
g[i]表示以i为终点时没有选择i节点的最大值
b状态转移方程
f[i]=g[i-1]+nums[i]

g[i]=max(g[i-1],f[i-1])+nums[i]
c初始化
f[0]=nums[0]
g[0]=0
d填表顺序
从左到右,两个表一起填
e返回值
max(f[n-1],g[n-1]);
n为nums大小
f代码
class Solution {
public:int massage(vector<int>& nums) {// 1. 创建⼀个 dp 表// 2. 初始化// 3. 填表// 4. 返回值int n = nums.size();if(n == 0) return 0; // 处理边界条件vector<int> f(n);auto g = f;f[0] = nums[0];for(int i = 1; i < n; i++){f[i] = g[i - 1] + nums[i];g[i] = max(f[i - 1], g[i - 1]);}return max(f[n - 1], g[n - 1]);}
};二、打家劫舍二
1、题目解析

第一道题契税就是这道题的变体,不同的是这道题多了一个要求——数组首尾相连
2、算法原理
a状态表示方程
经验+题目要求
dp[i]表示到这个i节点时最大的盗窃金额
但是这个值有两种情况,分别是选择了这个节点和没选择这个节点
f[i]表示i节点被盗窃时的最大金额
g[i]表示i节点没盗窃时的最大金额
这两者取的较大值就是dp[i]的值
但是这道题是一个环形数组,为了针对这一变数,有一个解决方法:
你不是环形数组嘛,说白了就是第一位被盗窃了和没被盗窃两种情况。
既然分了两种情况,我们进行两次盗窃,看哪次盗窃结果更大就行了。
偷盗了第一所房子——这就意味着1和n-1(第二位和最后一位不可以盗窃了),从第三位开始盗窃直到倒数第二位
没有盗窃第一所房子———这意味着需要从第一位盗窃至最后一位。
b状态转移方程
找到最近的节点划分问题
f[i]=g[i-1]+nums[i]

g[i]=max(g[i-1],f[i-1])+nums[i]
c初始化
f[0]=nums[0]
g[0]=0
d填表顺序
从左到右,两种情况分别填写两张表
e返回值
return max(rob1(nums,1,n-1),rob1(nums,2,n-2)+nums[0]);
3、代码
class Solution {
public:int rob(vector<int>& nums) {int n=nums.size();if(n==1)return nums[0];return max(rob1(nums,1,n-1),rob1(nums,2,n-2)+nums[0]); }int rob1(vector<int> nums,int left,int right){vector<int> f(right+1,0);vector<int> g(right+1,0);for(int i=left;i<=right;i++){f[i]=g[i-1]+nums[i];g[i]=max(f[i-1],g[i-1]);}return max(f[right],g[right]);}
};三、删除并且获得点数
1、题目解析

这道题就是将一个数删除然后获取这个数的点数,同时将+-1的数删除去补货的值,依次删除求获取的最大点数。
我们需要锻炼一种能力,将一道陌生的题目往我们熟悉的题目上联想————这其实不就是打家劫舍问题的变体吗,取一个值然后两两取值不能相邻。
这道题我们无法在原数组上获取数据,需要转换成一个行的数组arr,将每个数的和储存起来,通过下标来表示这个数,并且前后需要个例的数值一目了然

2、算法原理
a状态表示方程

b状态转移方程
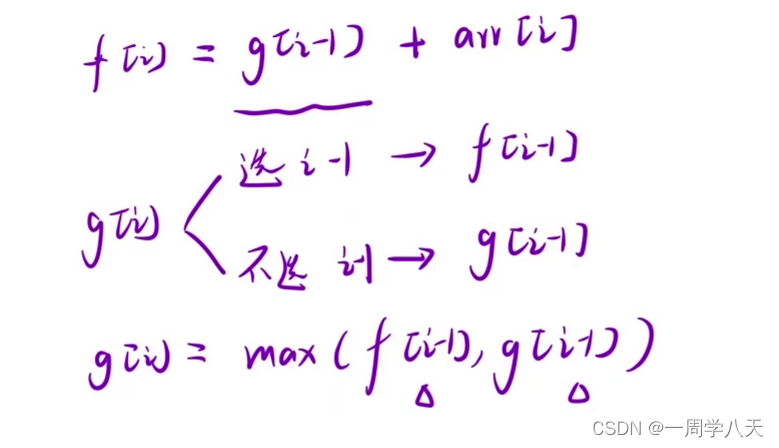
c初始化

d填表顺序

e返回值
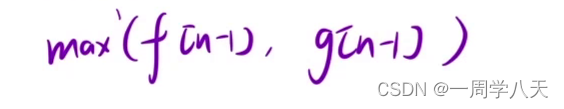
3、代码
class Solution {
public:int deleteAndEarn(vector<int>& nums) {//预处理//建表//初始化//填表//返回值int arr[10001]={0};for(int i=0;i<nums.size();i++){arr[nums[i]]+=nums[i];}int f[10001];int g[10001];f[0]=arr[0];g[0]=0;for(int i=1;i<=10000;i++){f[i]=g[i-1]+arr[i];g[i]=max(f[i-1],g[i-1]);}return max(f[10000],g[10000]);}
};四、粉刷房子
1、题目解析

题目的意思是给了我们一排房子,这一排房子不能刷上相同的颜色,让我们求最便宜的装修方案
题目给了我们一个二维数组,这个二维数组
这个二维数组从上到下写的是一个房子对应的颜色价格。
很多同学犯难了,不知道这个和动态规划有什么关联,或者不知道如何转化成动规问题。
就像动规的简化问题一样,我们需要问题转换成会写的问题来简化我们的问题。
我们写到过一道题下降路径最小和,我们将改题转换成这个问题。

将二维数组竖着看,表上横向写的是颜色对应的价格,竖向表示对应的楼房
2、算法原理
a状态表示方程
小技巧:经验+题目要求
dp[i][j]表示,到达该节点的时候,最小的专修价格。
b状态转移方程
小技巧:通规最近的一步简化问题
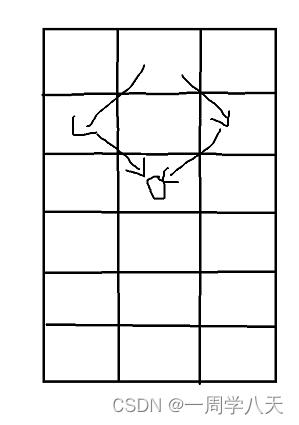
图中节点有且仅有两种可能,左上和右上这两种情况。
而这张图上也是两个节点对应的两个解决方法。
这其实也是这道题的影藏条件。
而dp[i][j]取值取两者较小值就行了。
c初始化
给dp第一排赋值即可
d填表顺序
从左到右,从上到下
e返回值
min(min(dp[m-1][0],dp[m-1][1]),dp[m-1][2])
3、代码
class Solution {
public:int minCost(vector<vector<int>>& costs) {int m=costs.size();vector<vector<int>> dp(m,vector<int> (3));dp[0][0]=costs[0][0];dp[0][1]=costs[0][1];dp[0][2]=costs[0][2];for(int i=1;i<m;i++){dp[i][0]=min(dp[i-1][1],dp[i-1][2])+costs[i][0];dp[i][1]=min(dp[i-1][0],dp[i-1][2])+costs[i][1];dp[i][2]=min(dp[i-1][0],dp[i-1][1])+costs[i][2];}return min(min(dp[m-1][0],dp[m-1][1]),dp[m-1][2]);}
};