此篇文章与大家分享分治算法关于归并排序的专题
对于归并排序在我个人主页专栏 <排序> 有详细的介绍
如果有不足的或者错误的请您指出!
1.归并排序
题目: 排序数组
1.1解析
关于归并排序的解析在我的个人主页<排序>专栏有详细的解释,理解归并排序对本专题的其他题目格外重要,一定要先理解归并排序的原理
本文直接画图说明:
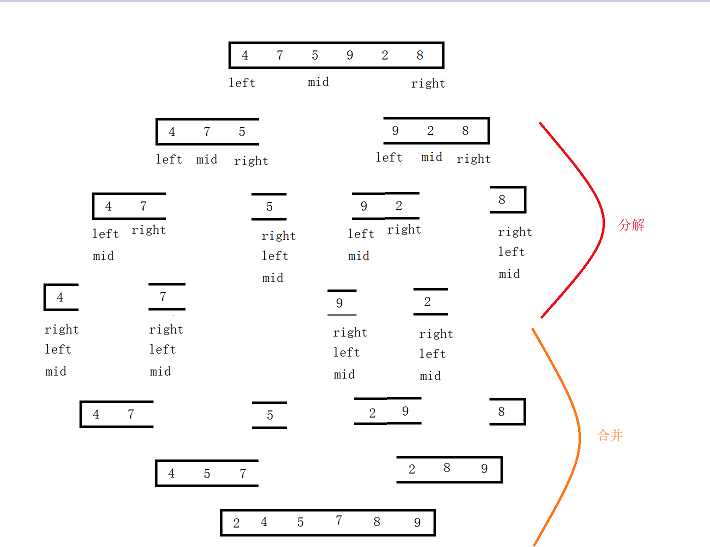
1.2题解
public class Test4 {int[] tmp;//将tmp数组设置为类属性时间复杂度更低public int[] sortArray(int[] nums) {tmp = new int[nums.length];mergeSort(nums,0,nums.length-1);return nums;}private void mergeSort(int[] nums,int left,int right){if(left >= right){return;}int mid = left + (right-left)/2;mergeSort(nums,left,mid);mergeSort(nums,mid+1,right);int i = 0;int cur1 = left;int cur2 = mid+1;while(cur1 <= mid && cur2 <= right){tmp[i++] = nums[cur1] > nums[cur2] ? nums[cur2++] : nums[cur1++];}while(cur1 <= mid){tmp[i++] = nums[cur1++];}while(cur2 <= right){tmp[i++] = nums[cur2++];}for(int j = left; j <= right; j++){nums[j] = tmp[j-left];}}
}2.数组中的逆序对
题目:数组中的逆序对
2.1解析:
如果我们通过暴力解法,就是两个两个枚举,但是时间复杂度太高了,在本题会超时
我们转变一下思路:
如果我们把数组划分维如图所示的两段区间,假设左区间的逆序对的数量为a,右边的逆序对的数量为b,再加上枚举左边一个右边一个元素的所有逆序对的情况为c,那么总逆序对的情况就是a + b + c;而左边区间和右边区间又各自可以分成两段区间…
举个具体例子:
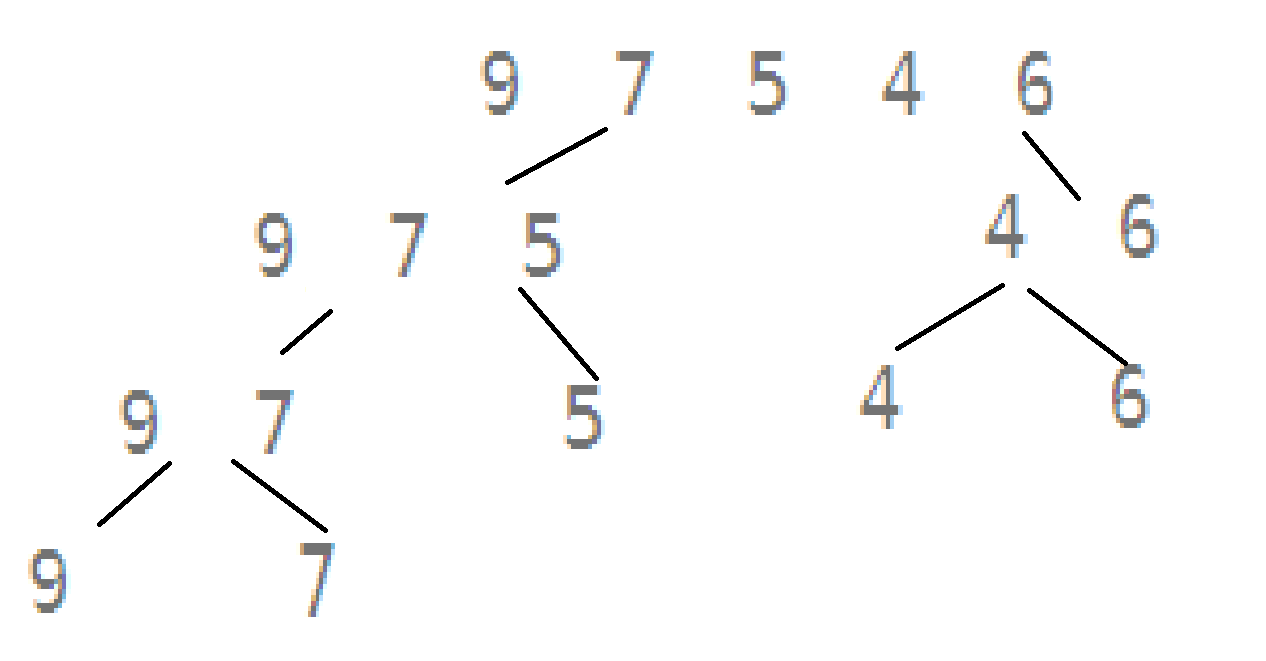
如图所示,我们用count来记录逆序对的个数,那么最后一层9 和 7,就是1组逆序对,count = 1; 9 7 和 5,可以组成 (9,5)和 (7,5),那么count = 3;
4和6不能组成逆序对;9 7 5 和 4 6,可以组成(9,4),(9,6),(7,4),(7,6),(5,4) ,那么count = 8
而上述每次分解成两段区间的过程不就是我们归并排序的分解过程嘛??
再者说,好像我们这样子分,到头来还是需要一一枚举,好像时间复杂度并没有很大的提示.但是我们实际上会发现一个细节:
我们在一一枚举的过程中并不关心左区间元素的顺序,也不关心右区间元素的顺序,我们每次只需要关心相对于左边的某个元素,在右边有多少个比这个元素小即可
那么我们就可以利用归并排序,将左右区间排序好

假设这是我们某段已经分别排好序的左右区间,排完序后我们找逆序对的时间复杂度就很低了
我们用变量cur2来遍历右区间,用变量cur1来遍历左区间
那么在定住cur2的时候,我们只需在左边从左到右找到第一个比2大的,就是3,那么,在左区间内3以后的所有数字,都可以和右区间的2组成逆序对,这样我们一下子就找出很多逆序对,不再需要一一枚举;接下来cur2++,但是cur1不需要回头重新从1开始遍历,因为我们的区间是递增的,而1 < 2,1就必然小于3,这就是排序给我们带来的很多好处
而当我们回顾一下归并排序的过程:我们也是用变量cur2来遍历右区间,用变量cur1来遍历左区间,当nums[cur1] <= nums[cur2]的时候,cur1++;反之cur2++,这不就恰好和我们上面分析的过程一模一样嘛???
因此我们只需要将上面的找逆序对的过程穿插在归并排序中间即可!不会给原归并排序带来时间复杂度的增加,因此时间复杂度还是O(N logN)!
理解完上面后,我们来拓展一个点
我们上面的数组是递增的,但是如果是递减呢??
那么此时我们应该是定住左边的元素,在右边找到第一个比这个元素小的,那么找到的这个元素之后的所有元素,都能和左边这个元素组成逆序对
2.2题解:
class Solution {private int count = 0;private int[] tmp;public int reversePairs(int[] record) {tmp = new int[record.length];mergeSort(record,0,record.length-1);return count;}private void mergeSort(int[] record,int left,int right){if(left >= right){return;}int mid = left + (right-left)/2;mergeSort(record,left,mid);mergeSort(record,mid+1,right);int cur1 = left;int cur2 = mid+1;int k = 0;while(cur1 <= mid && cur2 <= right){if(record[cur1] > record[cur2]){tmp[k++] = record[cur2++];count += mid - cur1 + 1;}else{tmp[k++] = record[cur1++];}}while(cur1 <= mid){tmp[k++] = record[cur1++];}while(cur2 <= right){tmp[k++] = record[cur2++];}for(int i = left; i <= right; i++){record[i] = tmp[i-left];}}
}
3.计算右侧小于当前元素的个数
题目:计算右侧小于当前元素的个数
3.1解析
实际上和我们上一道题的原理是一模一样的,但是这道题要我们返回的是数组就给我们带来了一定的难度
即题目要求我们返回的是数组,数组中存储的是给定数组对应元素的右侧小于当前元素的个数,而由于我们的原数组在归并排序中是一直在变的
解决方法就是哈希思想,但是我们采用哈希表,因为数组中可能会存在重复元素;
我们可以构建一个index数组,用来映射给定数组的下标,.当给定数组变了的时候,我们的index也要跟着变
3.2 题解
class Solution {int[] ret;int[] tmp;int[] tmpIndex;int[] index;public List<Integer> countSmaller(int[] nums) {ret = new int[nums.length];tmp = new int[nums.length];tmpIndex = new int[nums.length];index = new int[nums.length];for(int i = 0; i < index.length; i++){index[i] = i;}mergeSort(nums,0,nums.length-1);List<Integer> list = new ArrayList<>();for(int x : ret){list.add(x);}return list;}private void mergeSort(int[] nums,int left,int right){if(left >= right){return;}int mid = left + (right - left)/2;mergeSort(nums,left,mid);mergeSort(nums,mid+1,right);int cur1 = left;int cur2 = mid + 1;int k = 0;while(cur1 <= mid && cur2 <= right){if(nums[cur2] >= nums[cur1]){tmp[k] = nums[cur2];tmpIndex[k++] = index[cur2++];}else{ret[index[cur1]] += right - cur2 + 1;tmp[k] = nums[cur1];tmpIndex[k++] = index[cur1++];}}while (cur1 <= mid){tmp[k] = nums[cur1];tmpIndex[k++] = index[cur1++];}while(cur2 <= right){tmp[k] = nums[cur2];tmpIndex[k++] = index[cur2++];}for(int i = left; i <= right; i++){nums[i] = tmp[i-left];index[i] = tmpIndex[i-left];}}
}
4.翻转对
题目:翻转对
4.1解析
大体思路还是和我们前两题的思路是一样的,但是有一点特别的就是,.我们前两道题,无论是找逆序对还是找比当前元素小的个数,实际上都是单纯的两个数比大小,恰好和归并排序的过程吻合
但是我们这道题要比较的是两倍的关系,因此我们需要"合并"两次,第一次合并实际上并不是真正的合并,而是判断进行比较;第二次才是真正的合并
4.2题解
class Solution {int[] tmp;int count = 0;public int reversePairs(int[] nums) {tmp = new int[nums.length];merseSort(nums,0,nums.length-1);return count;}private void merseSort(int[] nums,int left,int right){if(left >= right){return;}int mid = left + (right - left) / 2;merseSort(nums,left,mid);merseSort(nums,mid+1,right);int cur1 = left;int cur2 = mid + 1;while(cur1 <= mid && cur2 <= right){while(cur2 <= right && nums[cur1] / 2.0 <= nums[cur2]){cur2++;}count += right - cur2 + 1;cur1++;}cur1 = left;cur2 = mid+1;int k = 0;while(cur1 <= mid && cur2 <= right){tmp[k++] = nums[cur1] > nums[cur2] ? nums[cur1++] : nums[cur2++];}while(cur1 <= mid){tmp[k++] = nums[cur1++];}while(cur2 <= right){tmp[k++] = nums[cur2++];}for(int i = left; i <= right; i++){nums[i] = tmp[i-left];}}
}
感谢您的访问!!期待您的关注!!!