1. 问题描述

gSpan 是一款图规则挖掘算法，目标是从现有的图集中挖掘频繁子图。如下图中包含三个图：

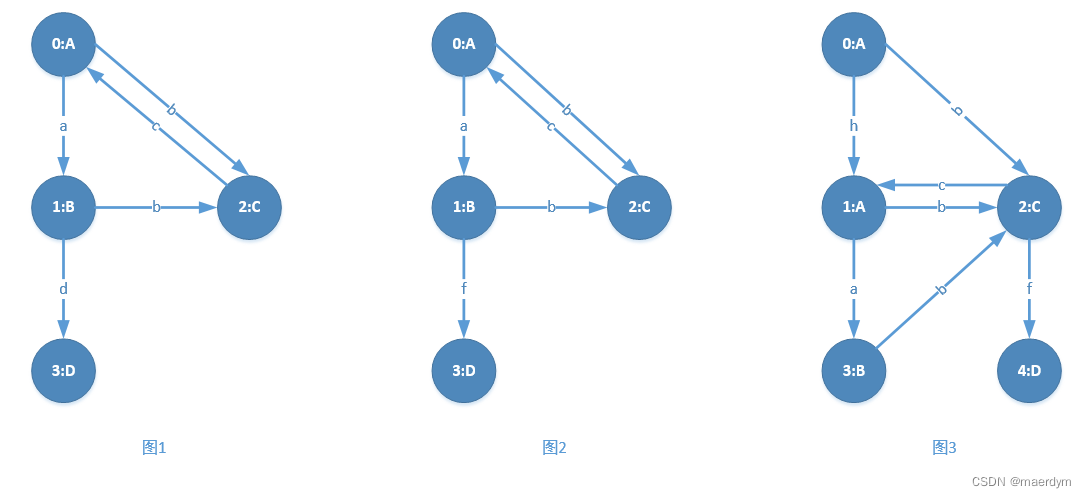
其中圆圈为顶点，连线为边，顶点包含两项信息：顶点表示和订单标签，如“0:A”表示顶点标识为0，顶点标签为A。边包含一项信息，即边的标签。
gSpan的目标是找出上述图集中所有的频繁子图（按标签进行查找）。例如将支持度设置为3，可以看出最大的频繁子图如下：

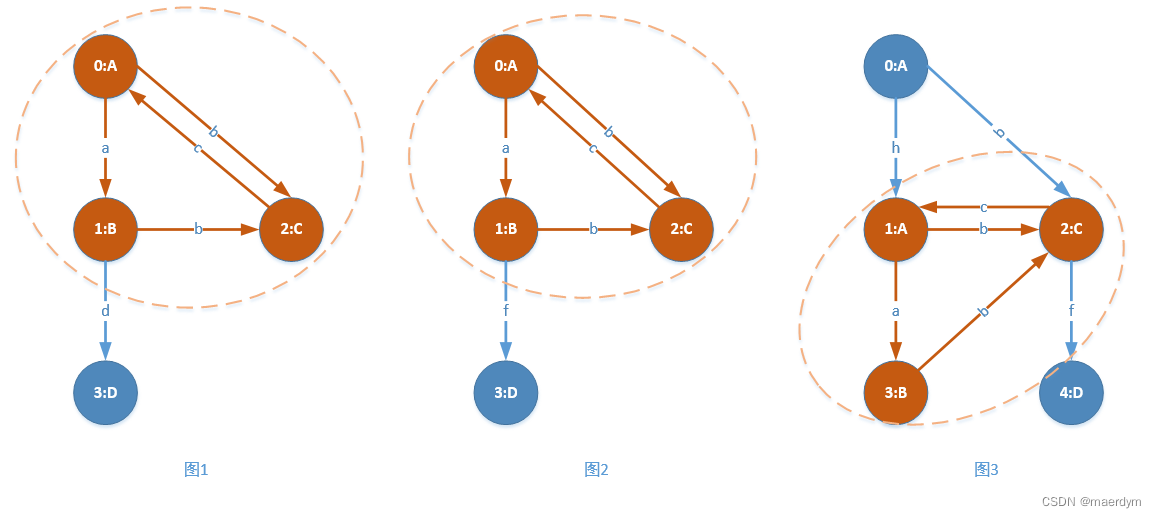
上图中只标注了最大频繁子图。

2. gSpan算法步骤

2.1 数据预处理

gSpan算法的首先会去除支持度小于设定阈值的顶点和边，因为如图某个顶点或某条边支持度小于设定阈值，那么包含这些点和这些边的子图支持度肯定也小于设定阈值。去除后得到的结果如下：

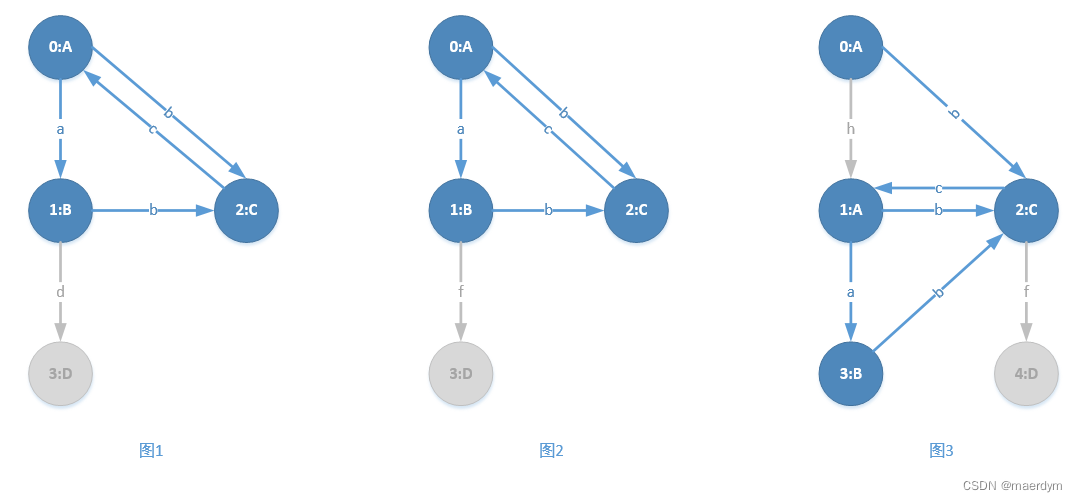
其中灰色的顶点和边为删除的顶点和边（虽然顶点D的支持度等于设定阈值3，但是没有边与顶点D相连因此删除顶点D）

2.2 深度递归挖掘频繁子图

2.2.1 获取所有的频繁边

遍历所有的图，构建边和所在图的映射字典，字典的key为以顶点标签和边的标签组成的三元组（<起始点标签,边标签,终止点标签>），value为该边所在的图的集合。例如边<A,a,B>,出现在图1，图2，图3中，则字典中key为<A,a,B>对应的value为数组“[图1，图2，图3]”。
通过上图构建的完整字典信息如下：

key(边)	Value（边所在的图组成的数组）
<A,a,B>	[图1，图2，图3]
<A,b,C>	[图1，图2，图3, 图3]
<B,b,C>	[图1，图2，图3]
<C,c,A>	[图1，图2，图3]

2.2.2 深度递归挖掘频繁子图

获取频繁边后，遍历频繁边，以频繁边作为起始边，并递归扩展边，查找频繁子图。边的扩展包括三种三种方式：

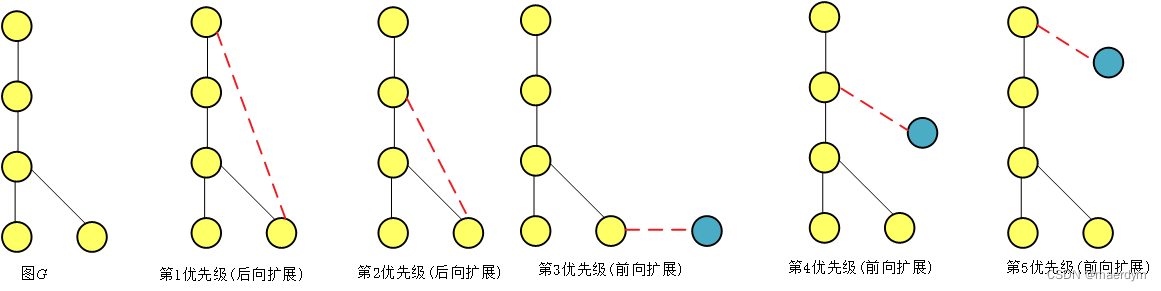
以边<A,a,B>为例：

• 第一优先级扩展的边为最右侧顶点到之前顶点的边，在<A,a,B>所在的图中查找顶点B到A的边，但所有图中均无此边，因此无第一优先级扩展边

• 因为只有两个订单因此不存在第二优先级

• 第三优先级为从最右侧端点B扩展出的边，遍历<A,a,B>所在的图，查找端点B扩展出的边为,可得：<B,b,C>，并记录该边所在的图[图1，图2，图3]

• 接着扩展第四优先级的边(因为只有两个订单，也没有第四优先级的边)

• 遍历<A,a,B>所在的图，查找顶点A扩展出的其他边，为：<A,b,C>，该边所在的图为[图1，图2，图3]

  共找到2条扩展边，且支持度均达到最小阈值：<B,b,C>和<A,b,C>
  
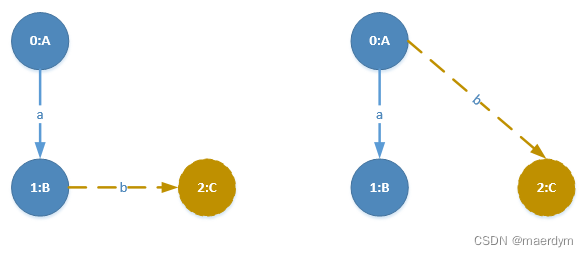
  先加入扩展边<B,b,C>,并继续扩展(在<A,b,B><B,b,C>所在的图中查找)：

• 第一优先级扩展边：查找C到A的边，为<C,c,A>,该边所在的图为[图1，图2，图3]

• 第二优先级扩展边：查找C到B的边，未找到对应的边，因此无第二优先级扩展边

• 第三优先级扩展边：从最右侧顶点扩展出的到其他边，未找到，因此无第三优先级扩展边

• 第四优先级扩展边：查找从顶点B扩展出的到其他边，未找到，因此无第四优先级扩展边

• 第五优先级扩展边：查找从从顶点A扩展出的到其他边，为<A,b,C>,其所在的图为[图1，图2，图3]

  
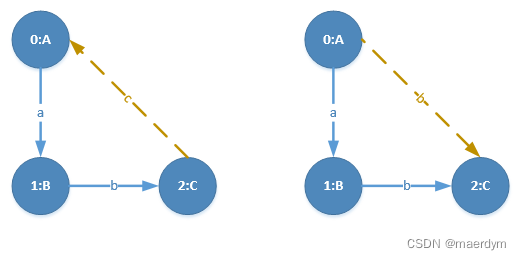
  共找到两条边：<C,c,A>,<A,b,C>,这两条边的支持度均达到最小阈值
  先加入<C,c,A>并继续扩展(在<A,a,B><B,b,C><C,c,A>所在的图中进行查找)

• 第一优先级：查找A到B的其它边，未找到

• 第二优先级：查找A到C的其它边，找到<A,b,C>，改边所在的图为[图1，图2，图3]

• 第三优先级：查找A出发的其它边，未找到

• 第四优先级：查找C出发的其它边，未找到

• 第五优先级：查找B出发的其它边，未找到

只找到一条边：<A,b,C>，且支持度达到最小阈值。

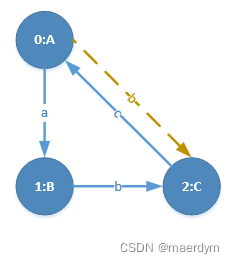
加入边<A,B,C>，并继续扩展，发现五个优先级扩展边都不存在，则退回上一步
在<A,a,B><B,b,C>中加入扩展边<A,b,C>,并继续扩展，以此类推，直到找出所有频繁子图。

参考文献

[1]. 数据挖掘之子图模式
[2]. gSpan频繁子图数据挖掘代码及原理解析