目录
一、买股票的最佳实际含冷冻期
1、题目解析
2、算法原理
a状态表示方程
b状态转移方程
c初始化
d填表顺序
e返回值
3、代码
4、感想
二、买股票的最佳时机函手续费
1、题目解析
2、算法原理
a状态表示方程
b状态转移方程
c初始化
d填表顺序
e返回值
3、代码
4、写题感悟
三、买卖股票最佳时机4
1、题目解析
2、算法原理
a状态表示方程
b状态转移方程
c初始化
d填表顺序
e返回值
3、代码
这篇文章每道题我都会以题目解析、算法原理、以及代码编写这三个模块进行讲解。
在算法原理这里,我们使用动态规划的解题模式进行讲解:
- 找出状态表示方程
- 找出状态转移方程
- 如何进行初始化
- dp表的填写顺序
- 该返回什么值
推荐从专题中的动态规划1开始进行训练,由浅入深
一、买股票的最佳实际含冷冻期
1、题目解析

这道题就是一个先买——>卖——>冷冻期——>买这三个过程然后期间可以选择何时卖也可以选择买,但是主体上就是按照这个流程来的。
而且通过示例二可以得出,只有一天交易的时候不要买入,不然会亏本
2、算法原理
a状态表示方程
经验+题目要求
dp[i]粗浅的表示当天结束后获得的最大利润
但是dp[i]会涵盖三种状态
- 买入状态——手上已经买入了股票
- 冷冻期状态——将股票卖出后进入的状态
- 可交易状态——经过冷冻期可以选择对当天股票是否买入的状态
这三种情况我们需要分别讨论,就需要三个表来表示。
因此状态表示方程应该是:
dp[i][0]表示第i天结束后,处于已买入状态的最大利润。
dp[i][1]表示第i天结束后,处于可交易状态的最大利润。
dp[i][2]表示第i天结束后,处于冷冻期状态的最大利润。
b状态转移方程
根据最近的一步划分问题
这道题目复杂的地方在于,最近的一步也有三种情况,我们要分别讨论前一天的三种情况怎么转换成今天的三种情况之一。
以转换成买入这种状态我们就需要讨论三种情况,
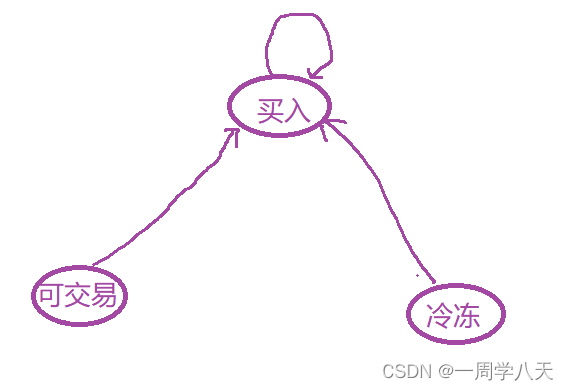
然后另外拉警钟情况都需要分别讨论,但其实有些情况是不可能达成的,以上面为例:
- 买入——>买入,啥事不做就可以达成了
- 冷冻——>买入,不可能达成,前一天结束时冷冻期意味着今天就是冷冻期。
- 可交易——>买入,前一天结束是可交易,那我今天买入股票,今天结束就是买入状态了。
所以最后只有这两种情况
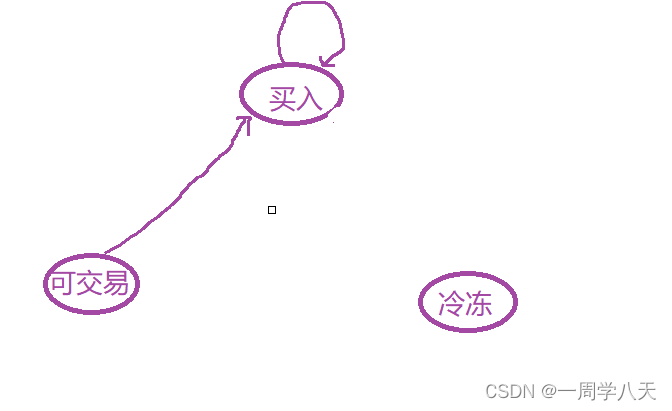
讨论完:
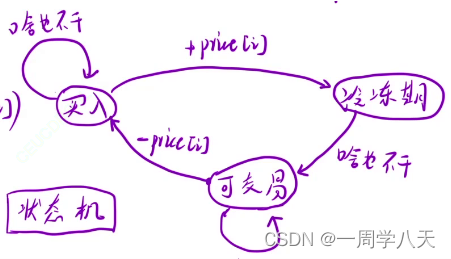
所以状态转移方程为:
dp[i][0]=max(dp[i-1][0],dp[i-1][1]-p[i])
dp[i][1]=max(dp[i-1][1],dp[i-1][2])
dp[i][2]=dp[i-1][0]+p[i]
c初始化
为了避免边界问题:
将dp[0][0],dp[0][1],dp[0][2]这三个值初始化,分别是:-p[i],0,0
d填表顺序
从左到右,每次每次填入上个表。
e返回值
返回最后一天三种情况最大值即可
3、代码
class Solution {
public:int maxProfit(vector<int>& prices) {//建表//初始化//填表//返回值int n=prices.size();int dp[n][3];dp[0][0]=0-prices[0];dp[0][1]=0;dp[0][2]=0;for(int i=1;i<n;i++){dp[i][0]=max(dp[i-1][0],dp[i-1][1]-prices[i]);dp[i][1]=max(dp[i-1][1],dp[i-1][2]);dp[i][2]=dp[i-1][0]+prices[i];}return max(max(dp[n-1][0],dp[n-1][1]),dp[n-1][2]);}
};4、感想
写到这道题的时候我感觉动态规划的解题方法是将所有情况穷举完了,然后选取最合适的值,尽管我们知道有些地方可以优化,但是这种穷举的方法反而可以帮我们解决处理这些优化地方的思考。
就像是返回值,我们直觉上会觉得返回值那天肯定不需要购入股票了,我们压根就不需要考虑这情况。但是站在代码的层面上考虑的话,就是多加了一个比较的是,这样还不需要我们去考虑一些特殊情况。
在写一道题目时侯我们可以根据示例,将一道题准确的得出最优解,但是要我们总结其中逻辑时却无从下手,因为情况太多了,反正你是一步接着一步,我把每一步的情况考虑清楚的话是可以选出我们需要的结果的,这其实也是一种剪枝思想的实现。
二、买股票的最佳时机函手续费
1、题目解析

相较于第一道题,这里有三种状态——买入后、卖出后、可买入。不过在一个完整的交易过程后需要扣除一个手续费。
2、算法原理
a状态表示方程
经验+题目要求
dp[i]粗浅的表示第i天后获得的最大利润
不过第i天有可能有三种情况,买入后、卖出后、可买入
经过分析:
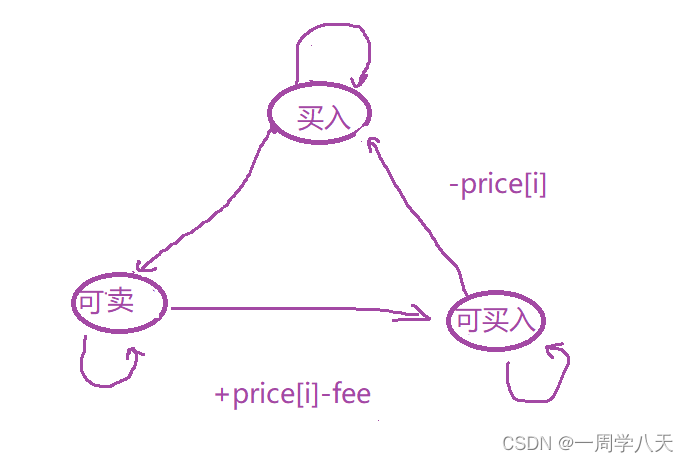
我们发现买入到达可买是没有任何数值变换的,所以其实这一种状态其实是没有 必要的。
简化成:

所以我们需要运营两个表:
dp[i][0]表示第i天结束后为未持有股票的情况下拥有的最高利润
dp[i][0]表示第i天结束后为持有股票的情况下拥有的最高利润
b状态转移方程
通过最近的一步简化问题。
分析可以得出
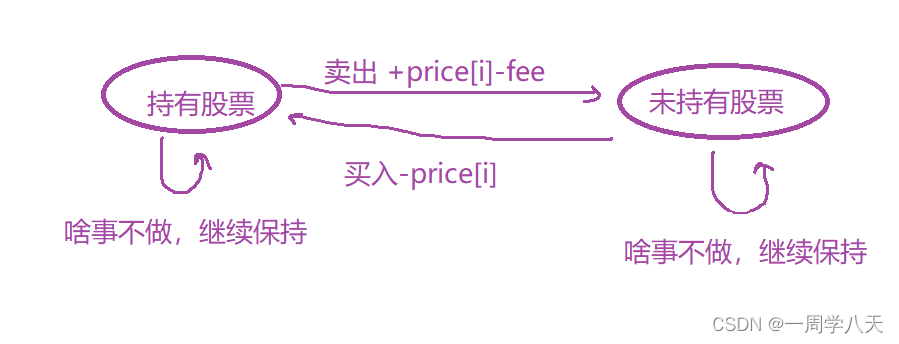
dp[i][0]有可能是

要想让我这一个i的值最大化,当然是要选择i-1值的最大情况
dp[i][1]有可能是:

c初始化
为了避免边界问题,考虑dp[0][0],和dp[0][1]即可
dp[0][0]=0
dp[0][1]=0-p[i]
d填表顺序
从左到右,两个表同时填
e返回值
max(dp[n-1][0],dp[n-1][1])
3、代码
class Solution {
public:int maxProfit(vector<int>& prices, int fee) {//建表//初始化//填表//返回值int n=prices.size();int dp[n][2];dp[0][0]=0;dp[0][1]=0-prices[0];for(int i=1;i<n;i++){dp[i][0]=max(dp[i-1][0],dp[i-1][1]+prices[i]-fee);dp[i][1]=max(dp[i-1][0]-prices[i],dp[i-1][1]);}return max(dp[n-1][0],dp[n-1][1]);}
};4、写题感悟
这种选择的思路感觉有点像是比较大小时,每次保存一个最小值
int my_min=0;
for(auto e:arr)
{if(my_min>e)my_min=e;
}
这道题是每次当前状态下最优解,你有更好的办法再来代替我
三、买卖股票最佳时机4
1、题目解析

2、算法原理
a状态表示方程
经验+题目要求
dp[i]粗浅的表示第i天结束后获得的利润最高
但是在第i天结束后又两种情况,手上持有股票、手上未持有股票。我们用两张表来表示:
f[i]表示第i天后持有股票时的最高利润
g[i]表示第i天后未持有股票时的最高利润
又这道题有一个附加条件,只最多只能进行k次交易。我们还有一种特殊状态需要维护、考虑,而且这种状态是影响每一天获取过程的。
所以我们通过一个二维数组表示这个状态转换方程:
f[i][j]表示第i天后持有股票的情况剩余j次交易机会的最高利润
g[i][j]表示第i天后未持有股票剩余j次交易机会的最高利润
b状态转移方程
还是那个小技巧:通过前一步,划分问题
最近的一步就是前一天,
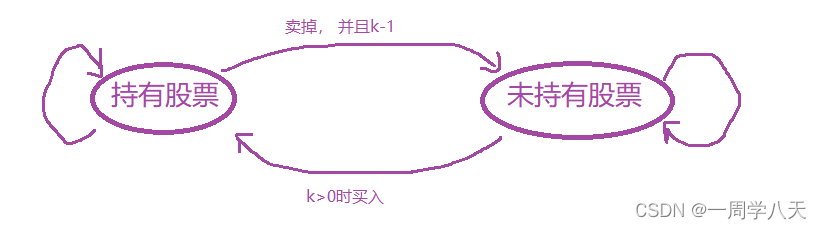
持有股票的状态需要前一天未持有股票的状态买入、或者前一天本身就持有股票
未持有股票的状态需要前一天持有股票的状态卖出、或者前一天本身就未持有股票
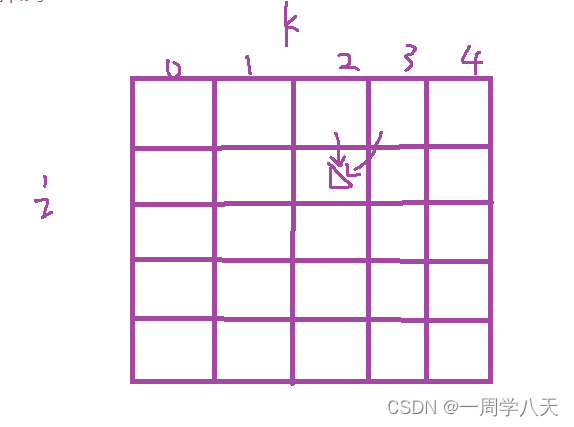
假设这个图是表示f[i][j]的,图中三角形的位置只会由上面和右上这两种情况得出。
由此可以得出状态转移方程:
f[i][j]=max(f[i-1][j],g[i-1][j]-prices[i])
g[i][j]=max(g[i-1][j],g[i-1][j+1]+prices[i])
c初始化
初始化需要解决的问题就是边界问题。
由状态转移方程可以观察出,容易出现边界问题的下标为i-1,j+1这两个地方。
所以我们需要对第一行和最后一列特殊处理。
for(int i=0;i<=k;i++){//对第一行进行特殊处理f[0][i]=0-prices[0];g[0][i]=0;}持有股票就减去价格,未持有就i为0
有同学可能会疑惑,为什么f[0][0]也可以这样赋值,应为它影响不到后续的结果,这样还使代码更加简洁。
最后一列我们进过特殊情况处理即可,在填写表格时:
for(int i=1;i<n;i++){for(int j=0;j<=k;j++){if(j==k){f[i][j]=max(f[i-1][j],g[i-1][j]-prices[i]);g[i][j]=g[i-1][j];continue;}f[i][j]=max(f[i-1][j],g[i-1][j]-prices[i]);g[i][j]=max(f[i-1][j+1]+prices[i],g[i-1][j]);}}d填表顺序
从左到右,同时填写两个表
e返回值
返回最后一天各个情况的最大值
int Max=INT_MIN;for(int i=0;i<=k;i++){int tem;tem=max(f[n-1][i],g[n-1][i]);Max=max(tem,Max);}return Max;3、代码
class Solution {
public:int maxProfit(int k, vector<int>& prices) {//建表//初始化//填表//返回值int n=prices.size();int f[n][k+1],g[n][k+1];f[0][0]=0;g[0][0]=0;for(int i=1;i<=k;i++){f[0][i]=0-prices[0];g[0][i]=0;}for(int i=1;i<n;i++){for(int j=0;j<=k;j++){if(j==k){f[i][j]=max(f[i-1][j],g[i-1][j]-prices[i]);g[i][j]=g[i-1][j];continue;}f[i][j]=max(f[i-1][j],g[i-1][j]-prices[i]);g[i][j]=max(f[i-1][j+1]+prices[i],g[i-1][j]);}}int Max=INT_MIN;for(int i=0;i<=k;i++){int tem;tem=max(f[n-1][i],g[n-1][i]);Max=max(tem,Max);}return Max;}
};