参考B站:09 Transformer 之什么是注意力机制(Attention)
1. 注意力机制(Attention)

红色的是科学家们发现,如果给你一张这个图,你眼睛的重点会聚焦在红色区域
人–》看脸
文章看标题
段落看开头
后面的落款
这些红色区域可能包含更多的信息,更重要的信息
注意力机制:我们会把我们的焦点聚焦在比较重要的事物上
Q、K、V
我(查询对象 Q),这张图(被查询对象 V),图中包含的模块(K)。
我看这张图,第一眼,我就会去判断哪些东西对我而言更重要,哪些对我而言又更不重要(去计算 Q 和 V 里的事物的重要度)
重要度计算,其实是不是就是相似度计算(更接近),点乘其实是求内积(数学中的原理,两个矩阵点乘得到的值越大,证明两个矩阵越相似。)
Q 、 K = k 1 , k 2 , ⋅ ⋅ ⋅ , k n Q、K=k_1,k_2,···,k_n Q、K=k1,k2,⋅⋅⋅,kn
通过点乘的方法计算Q 和 K 里的每一个事物的相似度,就可以拿到 Q 和
k 1 k1 k1的相似值 s 1 s1 s1,Q 和 k 2 k2 k2的相似值 s 2 s2 s2,Q 和 k n kn kn的相似值 s n sn sn.
进一步做 s o f t m a x ( s 1 , s 2 , ⋅ ⋅ ⋅ , s n ) softmax(s_1,s_2,···,sn) softmax(s1,s2,⋅⋅⋅,sn),便可以得到概率值 a 1 , a 2 , ⋅ ⋅ ⋅ , a n a_1,a_2,···,a_n a1,a2,⋅⋅⋅,an。
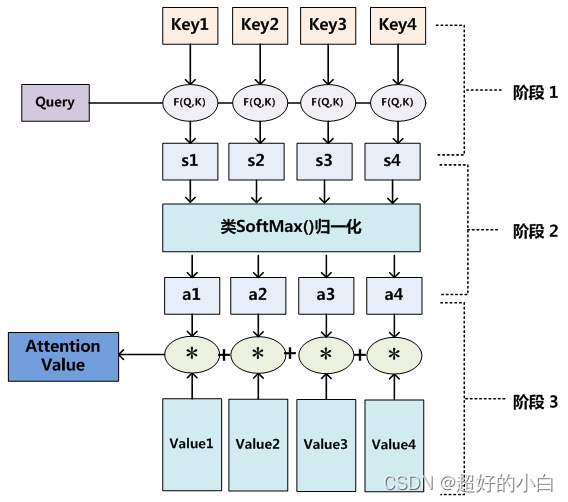
我们还得进行一个汇总,当你使用 Q 查询结束了后,Q 已经失去了它的使用价值了,我们最终还是要拿到这张图片的,只不过现在的这张图片,它多了一些信息(多了于我而言更重要,更不重要的信息在这里)。
V = ( v 1 , v 2 , ⋅ ⋅ ⋅ , v n ) = ( a 1 , a 2 , ⋅ ⋅ ⋅ , a n )•( v 1 , v 2 , ⋅ ⋅ ⋅ , v n ) = ( a 1 ∗ v 1 + a 2 ∗ v 2 + ⋅ ⋅ ⋅ + a n ∗ v n ) = V ′ V = (v_1,v_2,···,v_n)=(a_1,a_2,···,a_n)•(v_1,v_2,···,v_n)=(a_1*v_1 + a_2*v_2 + ··· + a_n*v_n )= V' V=(v1,v2,⋅⋅⋅,vn)=(a1,a2,⋅⋅⋅,an)•(v1,v2,⋅⋅⋅,vn)=(a1∗v1+a2∗v2+⋅⋅⋅+an∗vn)=V′
这样的话,就得到了一个新的 V’,这个新的 V’ 就包含了,哪些更重要,哪些不重要的信息在里面,然后用 V’ 代替 V。一般 K=V。
理解
注意力机制就是接收一个输入的东西(模型里面可能是特征),利用注意力机制找出图像中和该特征最相似的区域,该区域应该是提取出特征的区域,我们应该更加关注。
Transformer之自注意力机制(self-Attention)
Self-Attention 的关键点在于: K≈V≈Q 来源于同一个 X,这三者是同源的。
通过 X 找到 X 里面的关键点。
并不是 K=V=Q=X,而是通过三个参数 W Q , W K , W V W_Q,W_K,W_V WQ,WK,WV,接下来的步骤和注意力机制一模一样。
1.Q、K、V的获取
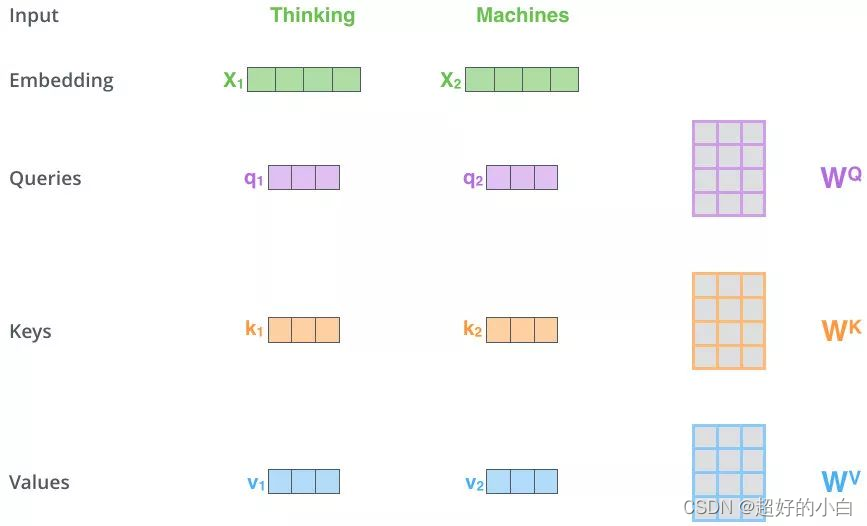
这里的 q 1 q_1 q1, q 2 q_2 q2 是由 x 1 x_1 x1, x 2 x_2 x2 与 W Q W_Q WQ 相乘得到的
, k 1 k_1 k1, k 2 k_2 k2 是由 x 1 x_1 x1, x 2 x_2 x2 与 W K W_K WK 相乘得到的
, v 1 v_1 v1, v 2 v_2 v2 是由 x 1 x_1 x1, x 2 x_2 x2 与 W V W_V WV 相乘得到的
这里的Q、K、V都来自于 x 1 x_1 x1, x 2 x_2 x2 ,所以是同源的。
2. Matmul (Q、K点乘,这里会和每个k进行点乘)
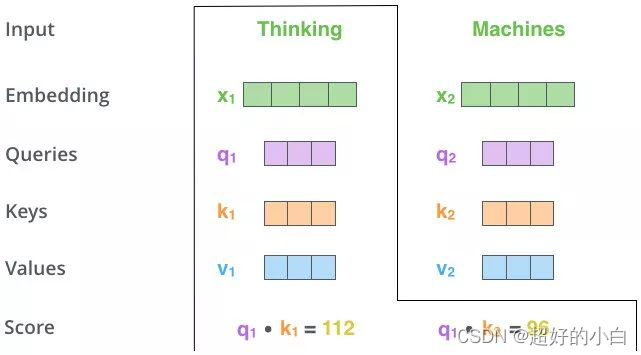
这里会先进行Q、K相乘,得到其相似值。
3.Scale+Softmax(对Q、K点乘结果进行softmax):
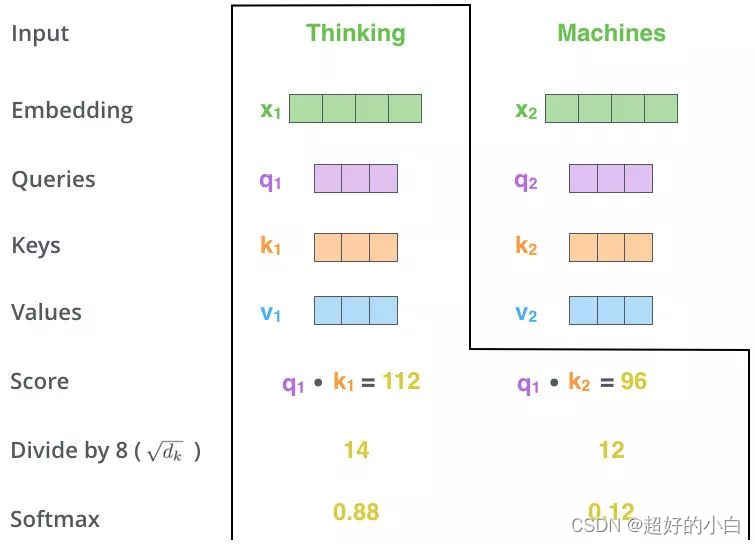
将Q、K相乘的相似值通过softmax,转为概率。
4. Matmul(得到的V1,并通过V1得到Z1):
将前面softmax得到的概率值0.88,再与 v 1 v_1 v1相乘, v 1 ∗ 0.88 v_1*0.88 v1∗0.88 得到一个新的向量值 v 1 v_1 v1。
此时的 v 2 v_2 v2的概率值是0.12, v 2 ∗ 0.12 v_2*0.12 v2∗0.12 得到一个新的向量值 v 2 v_2 v2。
最终的 z 1 = v 2 + v 2 z_1= v_2 + v_2 z1=v2+v2, z 1 z_1 z1 中包含了 v 1 v_1 v1和 v 2 v_2 v2的信息。
z 1 z_1 z1表示的就是 thinking 的新的向量表示,对于 thinking,初始词向量为 x 1 x_1 x1。
现在我通过 thinking machines 这句话去查询这句话里的每一个单词和 thinking 之间的相似度,新的 z 1 z_1 z1依然是 thinking 的词向量表示,只不过这个词向量的表示蕴含了 thinking machines 这句话对于 thinking 而言哪个更重要的信息。
举个例子:
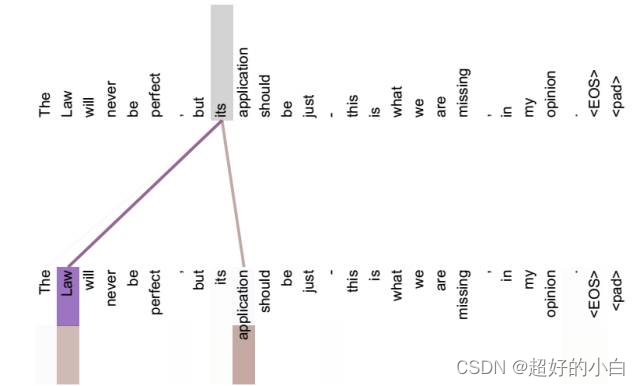
这里的 its 做了自注意力,其包含了这句话所有词的信息,并且对Law的相似度最高,所以这里的its最有可能代表its。
但是如果不做自注意力,这里的 its 就是单纯的三个字母 its,并没有包含任何信息。
也就是说 its 有 law 这层意思,而通过自注意力机制得到新的 its 的词向量,则会包含一定的 laws 和 application 的信息
自注意力矩阵表示:
Q 、K、V的获取
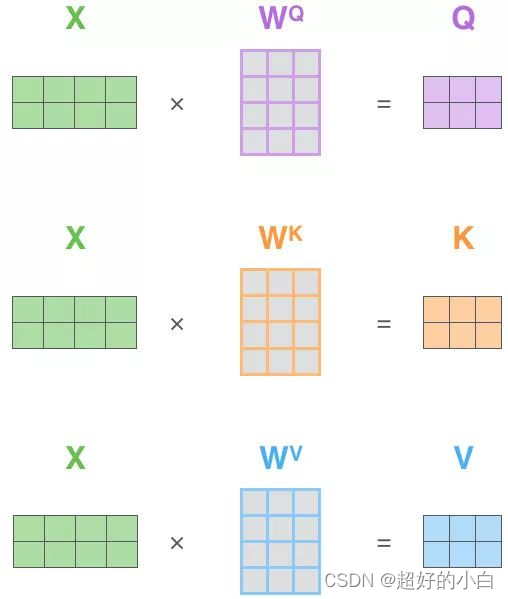
Z矩阵的获取
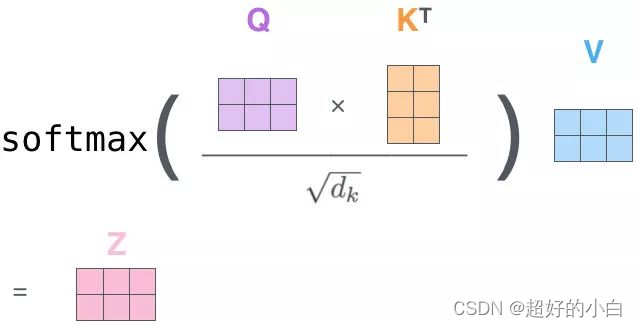
Z矩阵的表示

最终Z矩阵中就有每个单词和每个单词联系的概率值。






![[开源] 基于GRU的时间序列预测模型python代码](https://img-blog.csdnimg.cn/direct/b4eda21ff10944fba9afff8afc864c23.png)