39.组合总和

区别：同一个数字可以无限制重复被选取！

所以树形结构中，选择一个数，剩余集合也要带上选了的那个数！—下一层递归还是传i

剪枝：对数组排序，一进for循环就判断是否sum + candidates[i] > target，是就直接break

• 全局变量：二维数组result 一维数组path

1. 递归函数

void backtracking(candidate,target,sum,startIndex)

2. 终止条件

if(sum > target) return;
if(sum == target) {  //找到了一个目标组合result.add(new ArrayList<>(path));return;
}

3. 单层递归逻辑

这里的i就是数组的下标！candidate[i] 。startIndex从0开始！（代表下标）

进入下一层递归时传的还是i才能保证 本层使用了之后，下一层还要也要带上这个数

startIndex是当前层的最开始，backTracking传入的startIndex是死的，但是当前层还需要进行自己后续的for循环，所以得用i，因为I是不断++的

for(int i = startIndex; i < candidate.size(); i++) {path.add(candidate[i]);sum += candidate[i];backtracking(candidate,target,sum,i);  //注意下一层递归传的还是ipath.remove(path.size()-1);sum -= candidate[i];
}

4. 剪枝

本题如何剪枝？先对数组进行排序，一进for循环就先判断，如果本层的 sum + candidates[i]）已经大于target，就可以直接结束for循环的遍历，没必要进入下一层递归了，break出for循环（再往后累加只会更大）

• 完整代码

class Solution {List<List<Integer>> result = new ArrayList<>();List<Integer> path = new ArrayList<>();public List<List<Integer>> combinationSum(int[] candidates, int target) {Arrays.sort(candidates);backtracking(candidates, target, 0, 0);return result;}void backtracking(int[] candidates, int target, int sum, int startIndex) {if(target == sum) {result.add(new ArrayList<>(path));return;}for(int i = startIndex; i < candidates.length; i++) {if(sum + candidates[i] > target) break;path.add(candidates[i]);sum += candidates[i];backtracking(candidates, target, sum, i);path.remove(path.size()-1);sum -= candidates[i];}}
}

40.组合总和 II

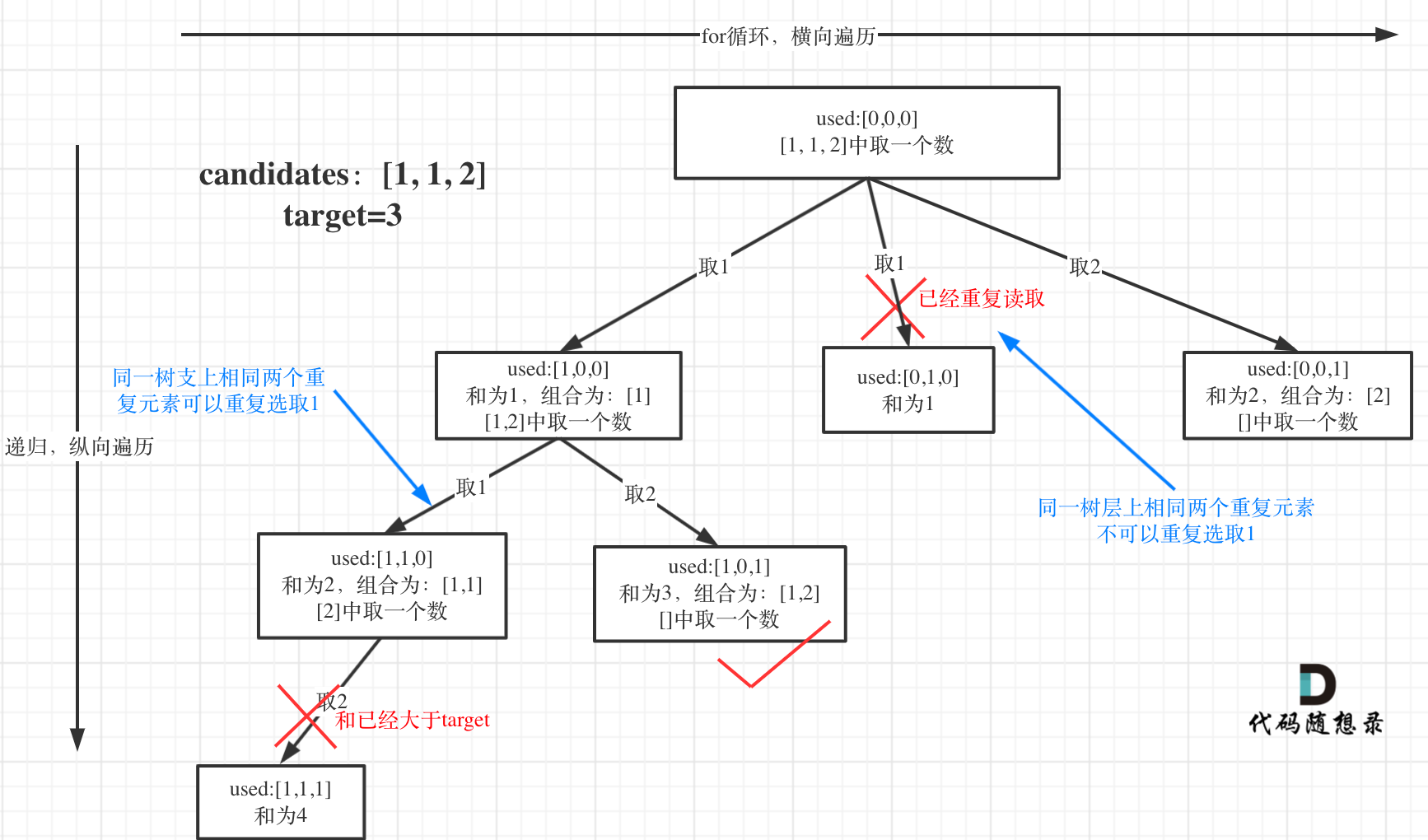
• 区别：给的数组中有重复元素。比如[1,1,7] 我们要进行去重，不然会出现两个[1,7]！

怎么去重？在搜索的过程中去重。重复过的元素不能再用了

两个维度：树层去重，树枝去重 树枝去重是指组合中不能有一样的元素，是可以有的！我们要的是树层去重

需要一个数组used告诉我们哪个元素使用过，下标对应原数组，用过就变为1

先对数组排序，这样相同的元素就在一起了！第一个1搜索过了，第二个1就没必要去搜索了，直接跳过！

• 具体是在for循环里，if(i>0 && nums[i]==nums[i-1] && used[i-1]==0) continue;跳过这个元素往后取

used[i-1]=0说明前一个和它相等的元素没有被用过，此时是树层去重！否则就是两个[1,7]了。(used[i-1]=1为什么不行？这样就是两个都用的情况，[1,1,7])

• 或者：直接if (i > starIdex && candidates[i - 1] == candidates[i]) continue; 可以不用used数组！

class Solution {List<List<Integer>> result = new ArrayList<>();List<Integer> path = new ArrayList<>();public List<List<Integer>> combinationSum2(int[] candidates, int target) {int[] used = new int[candidates.length];Arrays.sort(candidates);Arrays.fill(used, 0);backtracking(candidates,target,0,used,0);return result;}void backtracking(int[] candidates, int target, int sum, int[] used, int startIndex) {if(sum > target) return;if(target == sum) {result.add(new ArrayList<>(path));return;}for(int i = startIndex; i < candidates.length; i++) {if(i > 0 && candidates[i] == candidates[i-1] && used[i-1]==0) continue;path.add(candidates[i]);sum += candidates[i];used[i] = 1;backtracking(candidates, target, sum, used, i+1);path.remove(path.size()-1);used[i] = 0;sum -= candidates[i];}}
}

131.分割回文串

和组合问题是类似的。怎么类似？例如"abcdef" 一开始分割a，接下来分割bcdef。再分b，a|b|cdef

两个分割之间的区间组成了一个子串

回溯的过程其实是求出所有分割子串的可能方案！然后对所有的可能判断每一个子串是否是回文串

两个全局变量path和result。startIndex就是切割线（从0开始）。

我们把判断回文子串的逻辑放在了单层搜索里。如果不是回文就不会进入下一层的递归！

如何表示每一个子串？[startIndex，i] i代表当前切割点，index代表上一个切割点

1. 递归函数

void backtracking(String s, int startIndex)

2. 递归终止条件

//切割到字符串最后了，如果起始位置大于等于s的大小，说明找到了一组分割方案
if(startIndex >= s.length()) {lists.add(new ArrayList(deque));  //一定都是回文串了，直接收集return;
}

3. 单层搜索逻辑

for(int i = startIndex; i < s.length(); i++) {if(isPalindrome(startIndex,i,s)) {String str = s.substring(startIndex, i + 1);  //substring是左闭右开！path.add(子串);} else continue;  //直接跳到下一个i，不会进入下一层递归backtracking(s,i+1);path.remove(path.size()-1);
}

4. 判断子串是否回文的函数

boolean isPalindrome(int left, int right, String s) {for(int i = left,j = right; i < j; i++,j--) {if (s.charAt(i) != s.charAt(j)) {return false;}}return true;
}

• 完整代码

class Solution {List<List<String>> result = new ArrayList<>();List<String> path = new ArrayList<>();public List<List<String>> partition(String s) {backtracking(s,0);return result;}void backtracking(String s, int startIndex) {if(startIndex >= s.length()) {result.add(new ArrayList<>(path));return;}for(int i = startIndex; i < s.length(); i++) {if(isPalindrome(startIndex,i,s)) {  //如果不是回文子串 直接跳到i+1，不会进入递归path.add(s.substring(startIndex,i+1));} else continue;backtracking(s, i+1);path.remove(path.size()-1);}}//判断回文子串boolean isPalindrome(int left, int right, String s) {for(int i = left,j = right; i < j; i++,j--) {if(s.charAt(i) != s.charAt(j)) {return false;}}return true;}
}

Day 27总结

1. 虽然都是一进for循环里就判断，但一个是continue一个是break！continue代表跳到下一个i+1开始搜，不进入下一层递归。break代表直接结束整个for循环，终止搜索！

2. 初始化used数组可以用Arrays.fill()

3. 切割回文串问题要联想到组合问题，startIndex相当于切割线，终止条件就是起始位置≥s的长度。在单层逻辑里判断是不是回文串，是就直接substring收集子串，不是就continue（直接跳到下一个i，不会进入下一层递归）。这样可以直接在终止条件里收集path了。

4. substring是左闭右开！！

5. 判断回文串isPalindrome，用i和j两边夹击。

6. 如果要求这一位元素不能重复用，递归时传i+1，可以重复用（如39）就传i！