目录
- 文本输入处理
- 词向量
- 位置向量
- 编码器 Encoder
- Self-Attention
- 多头注意力机制
- 残差连接
- 解码器 Decoder
- 线性层与Softmax
- 损失函数
- 总结与心得体会
这周来看一下Transformer是怎么将文本转换成向量,然后又输入到模型处理并得到最终的输出的。
文本输入处理
词向量
和常见的NLP任务一样,我们会先使用词嵌入(Embedding)算法,将文本序列转换成词向量。实际应用中的向量维数很高,不方便演示,以4维的词向量为例。
于是当我们输入的文本中有3个词时,就会生成三个维度为4的向量。
而在实际的应用过程中,我们会同时给模型输入多个句子,如果每个句子的长度不一样,模型就没有办法批量处理了,所以这里会有一个pad操作,选择一个合适的最大长度,达不到的用0填充,超出的进行截断。
最大序列长度是一个超参数,通常希望越大越好,但是更长的序列会占用更大的显存,所以还是要权衡。
位置向量
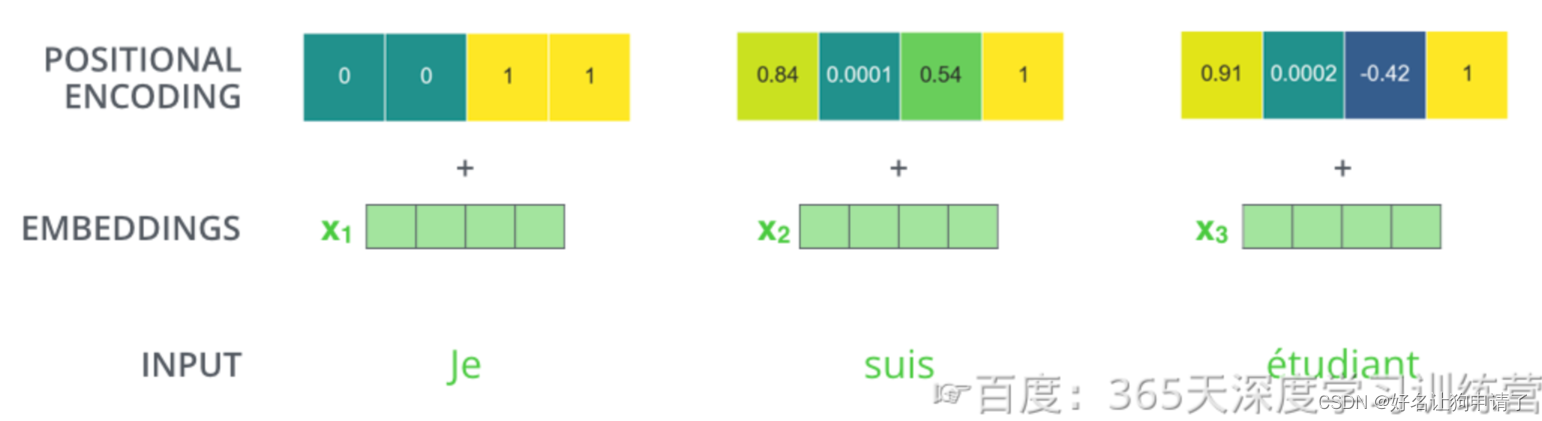
输入序列中的每个单词被转换成词向量后,还需要加上位置向量才能得到该词的最终向量表示。
Transformer对每个输入的词向量都加上了位置向量。这些向量有助于确定每个单词的位置特征、句子中不同单词之间的距离特征。
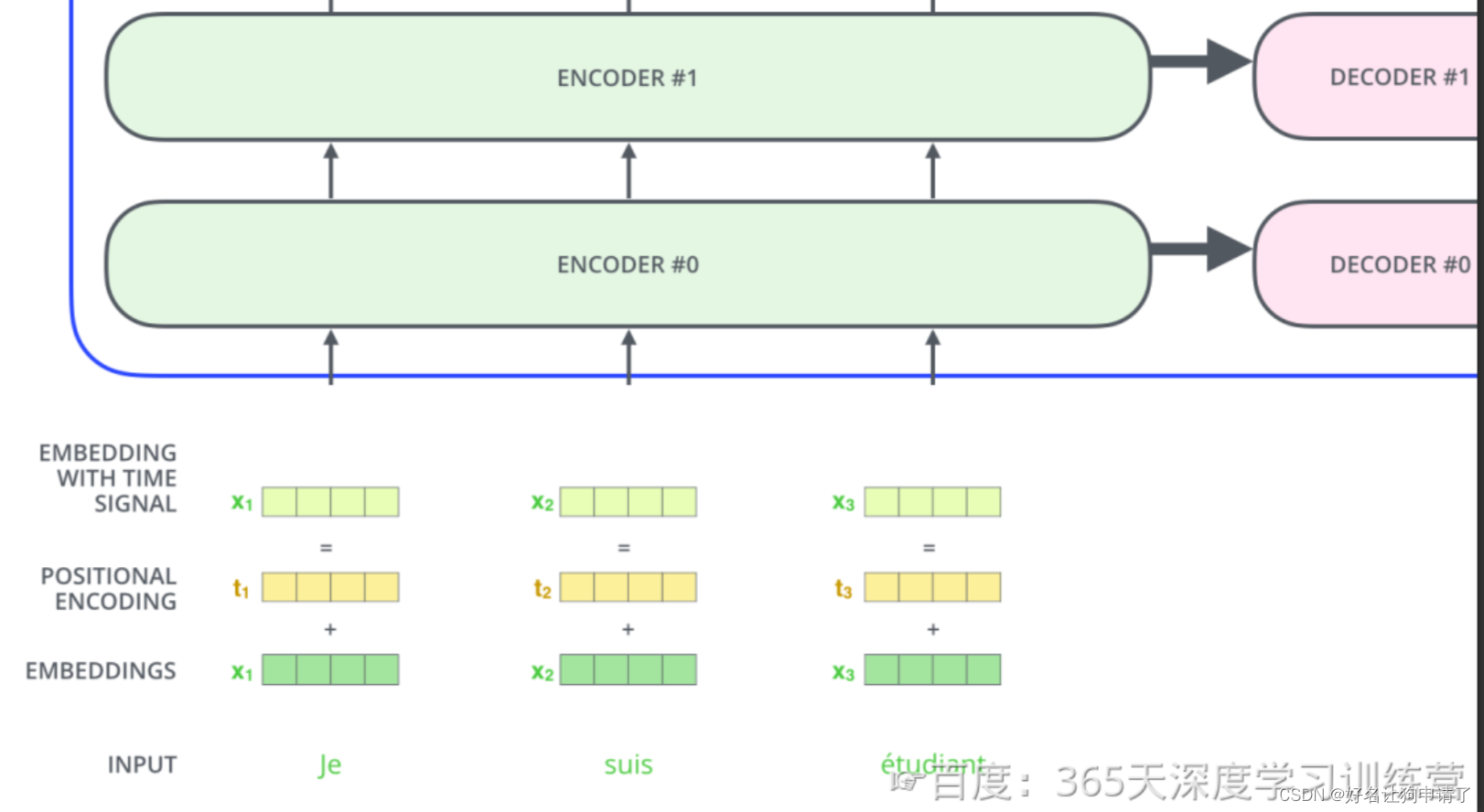
假设词向量和位置向量的维度是4,下图展示了一种可能 的位置向量+词向量。
编码器 Encoder
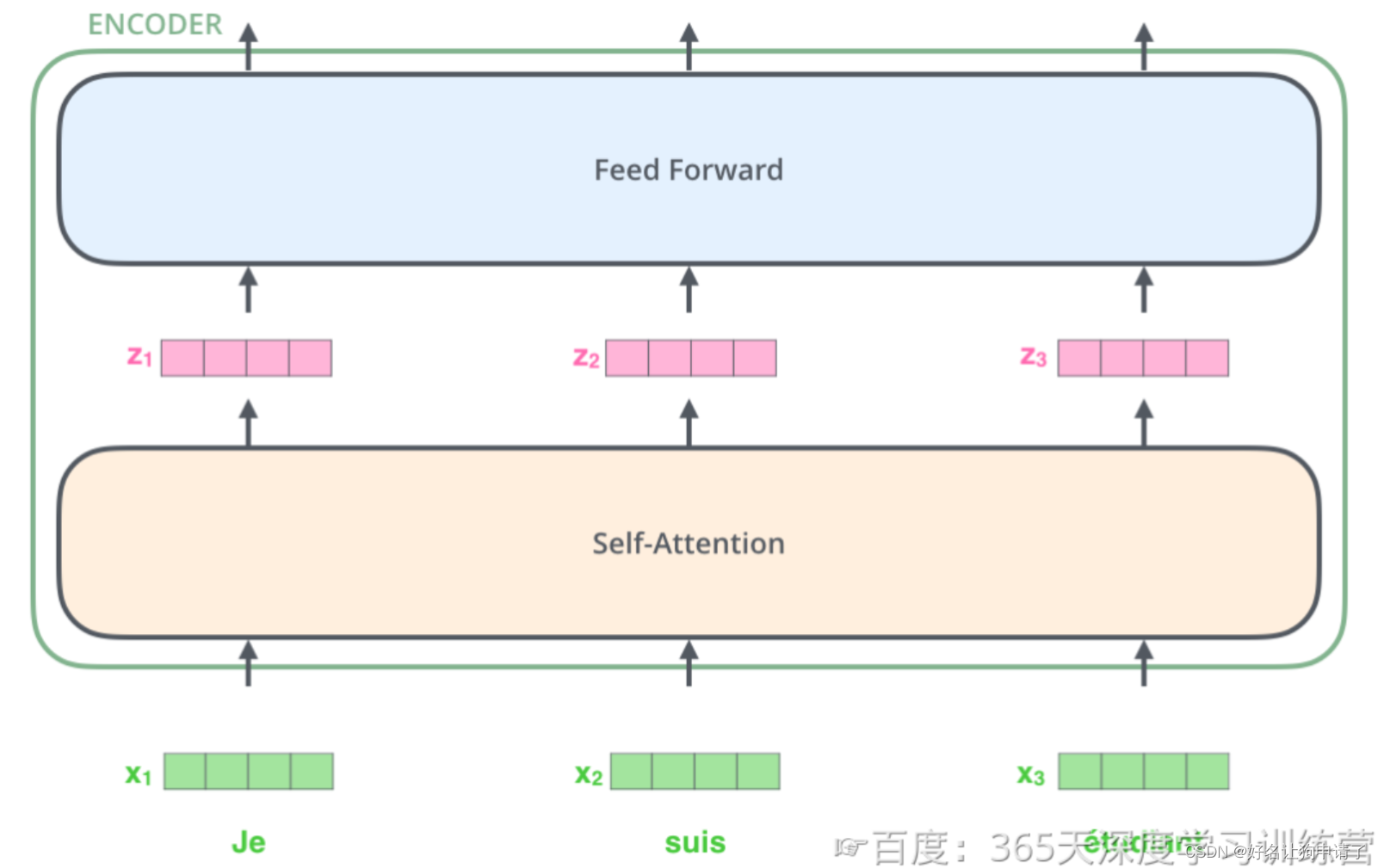
编码器的输入是经过上一步的文本输入处理后的向量,这个向量将从编码器的第一层开始,第一层编码器输出的同样是一样向量序列,然后以此类推再送入下一层编码器。如图所示,在第一层中,向量先进入Self-Attention块,然后进入FFN神经网络,最后得到当前层的新向量作为输出。
Self-Attention
自注意力机制就是使用向量与自己进行注意力计算,通过一个nxn的矩阵来进行,得到每个词向量对句中所有词向量的注意力分数,然后将注意力分数应用到原向量中,得到注意力模块的输出
多头注意力机制
通过多次并行的计算,得到一组向量的结果,然后再合并,可以得到表示能力更强的向量。
多头注意力机制在两个方面增强了Attention层的能力:
- 扩展了模型关注不同位置的能力。
- 多头注意力机制赋予Attention层多个“子表示空间”。
残差连接
模型计算得到self-attention输出后,单层的encoder后续还有两个重要的操作:残差连接和标准化。
编码器的每个子层(一个完整的Self-Attention+FFN)都有一个残差连接和层标准化(LayerNormalization),如图。
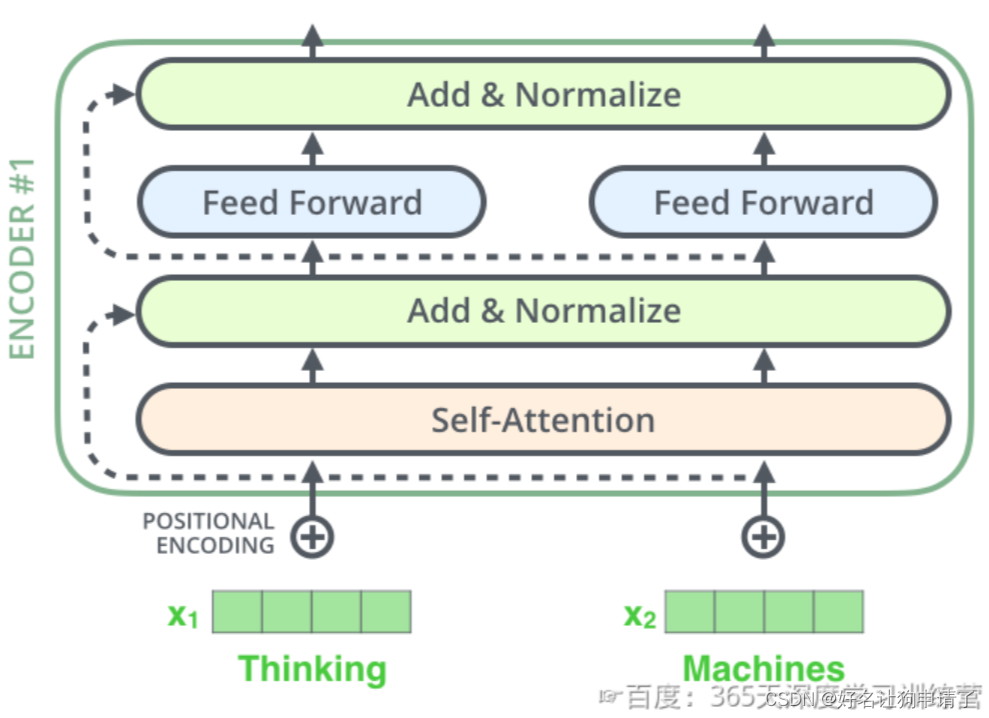
更细粒度的图如下:
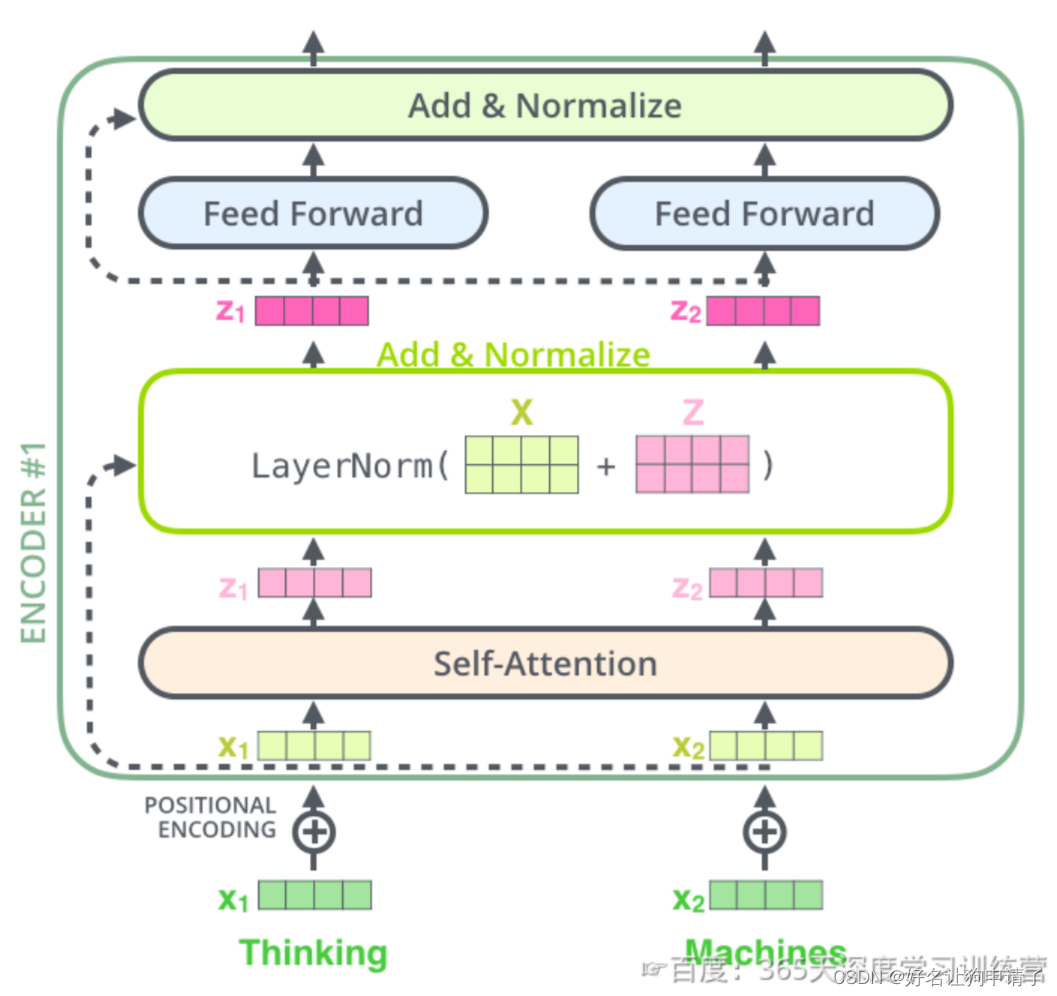
这一特性不仅在编码器中应用,也被应用到了解码器中。
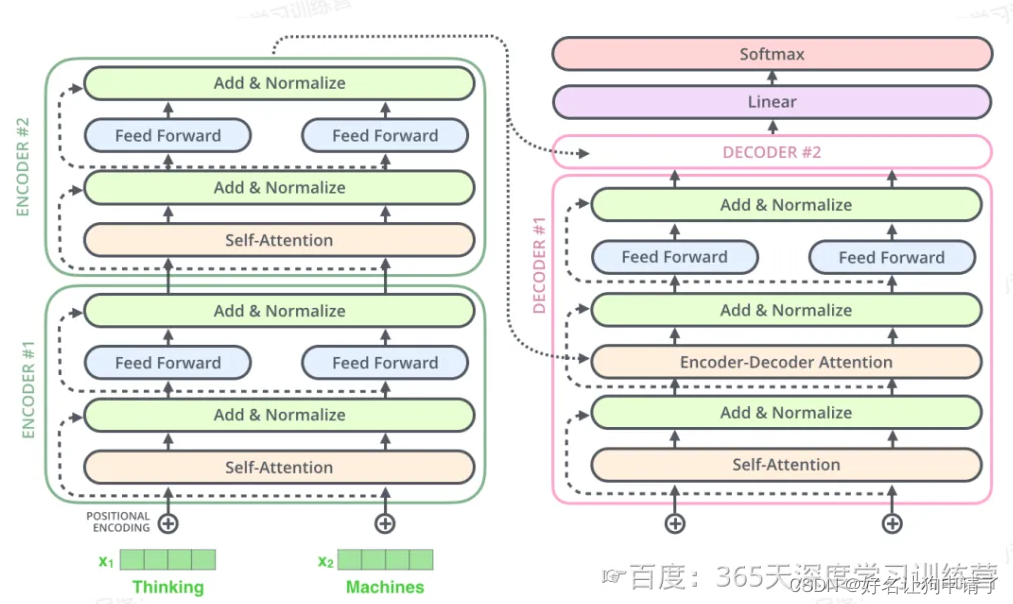
解码器 Decoder
和一般的模型不同的是,解码器的输入也是一个序列文本,和编码器一样。
而编码器的输出会输入到编码器的Encoder-Decoder-Attention层中,与解码器输入的向量进行计算。
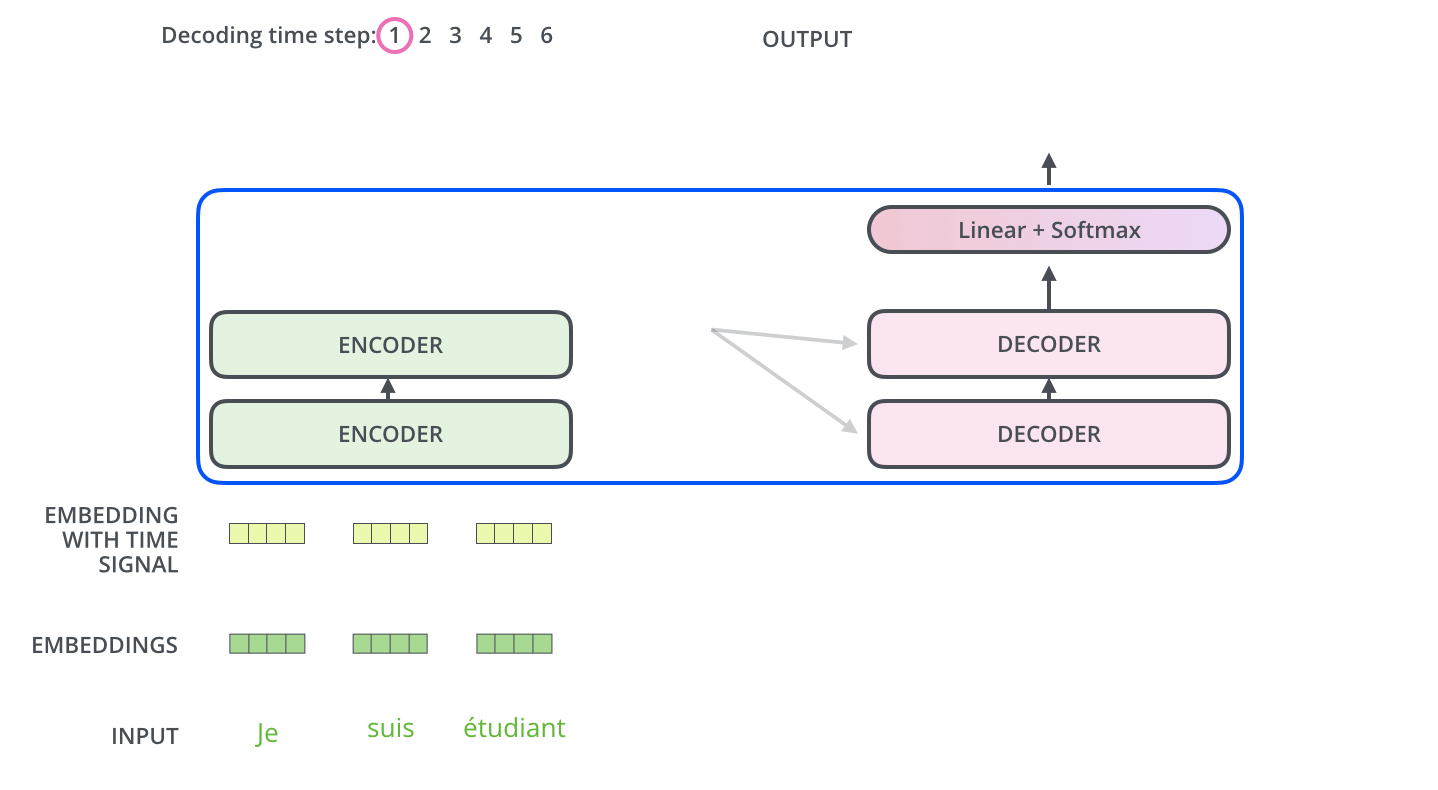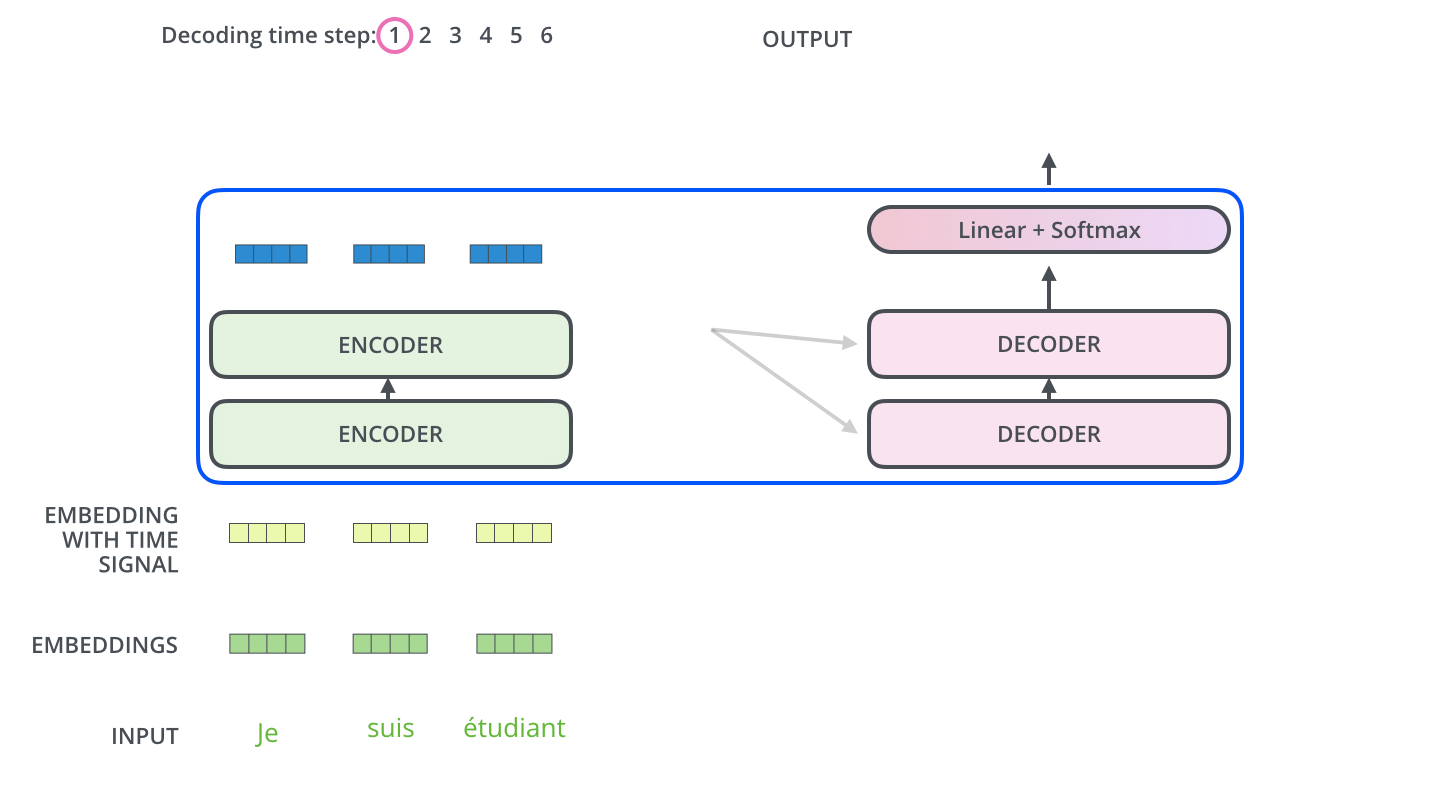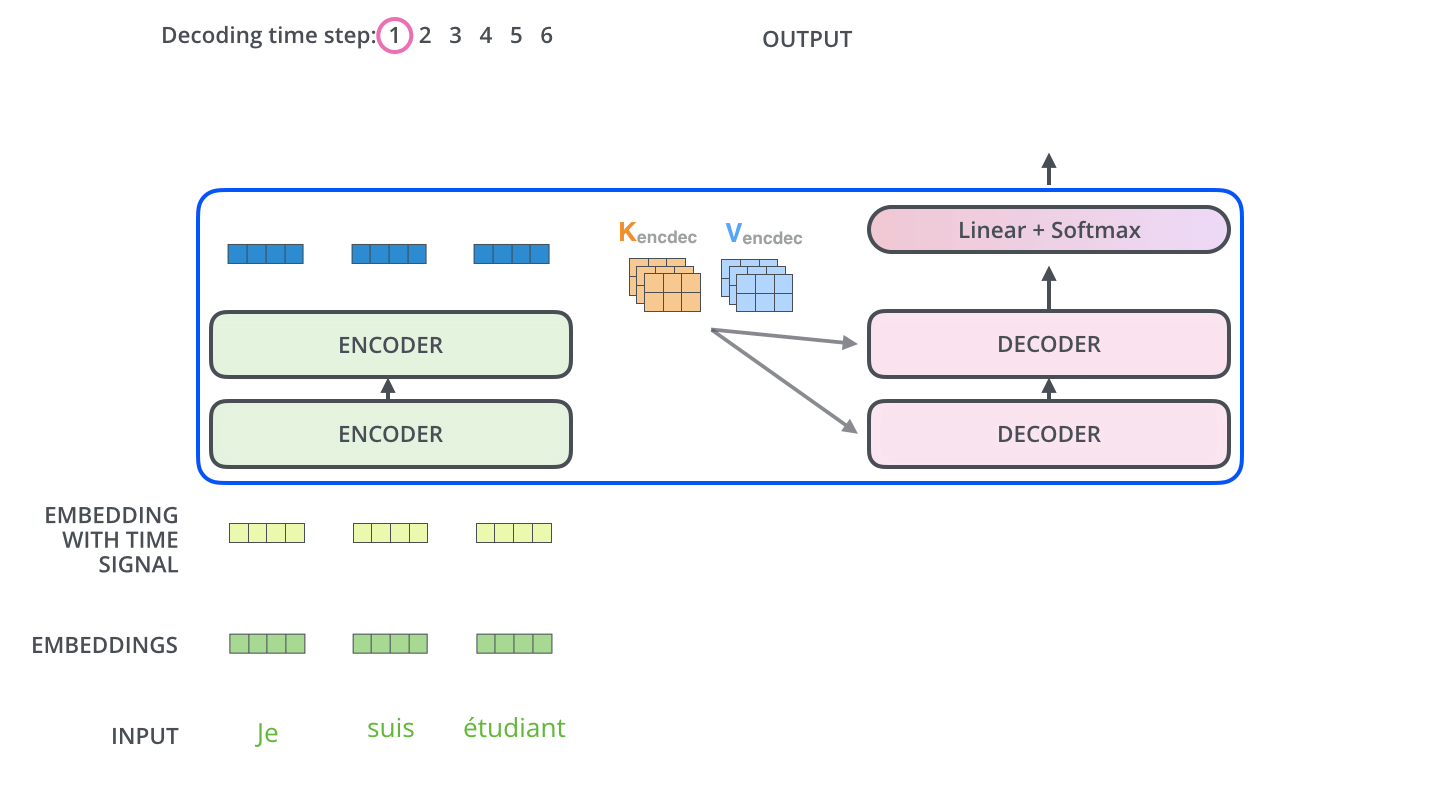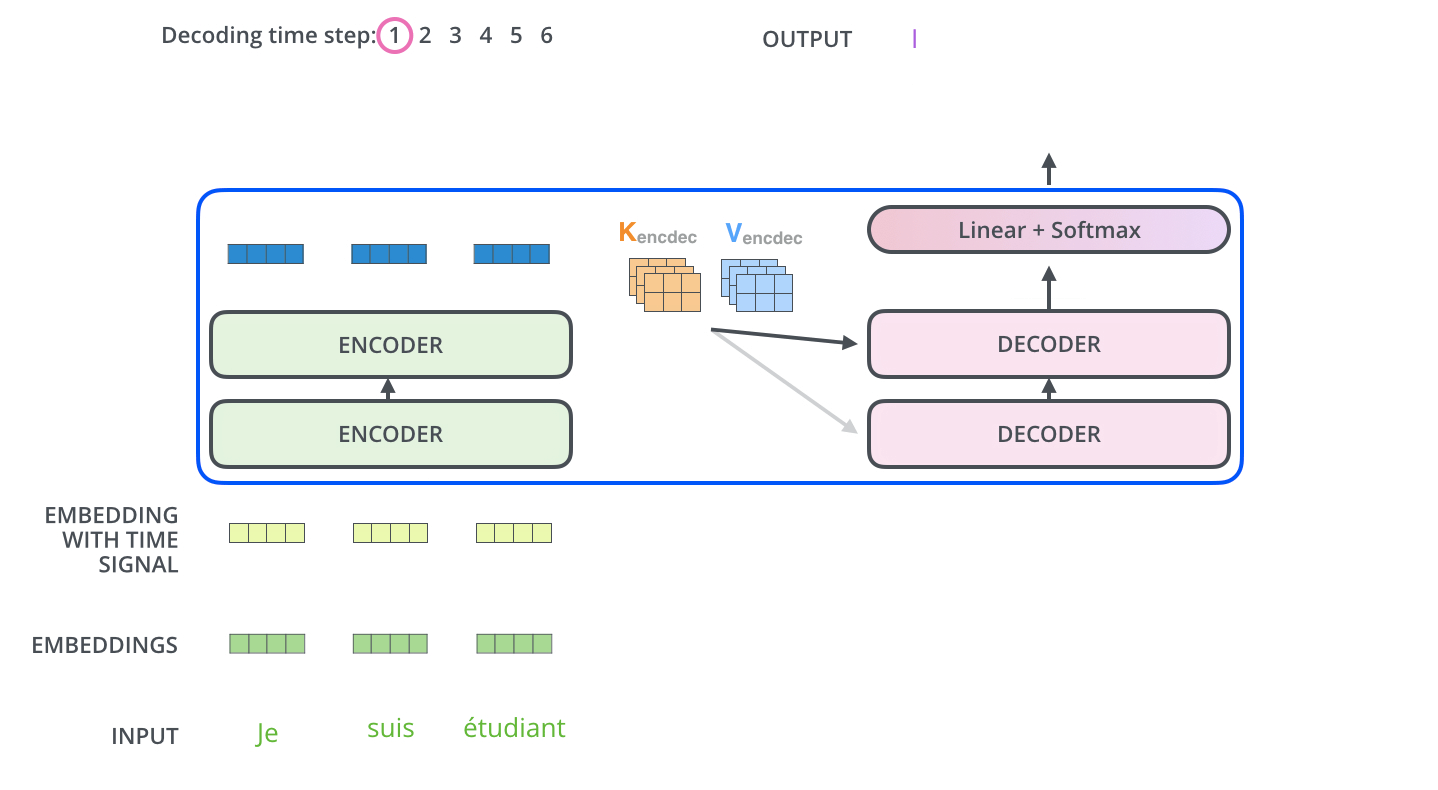
解码阶段的每一个时间步都输出一个翻译后的单词,然后这个单词又输入到下一个时间步的解码器,重复这个过程,直到输出一个结束符。
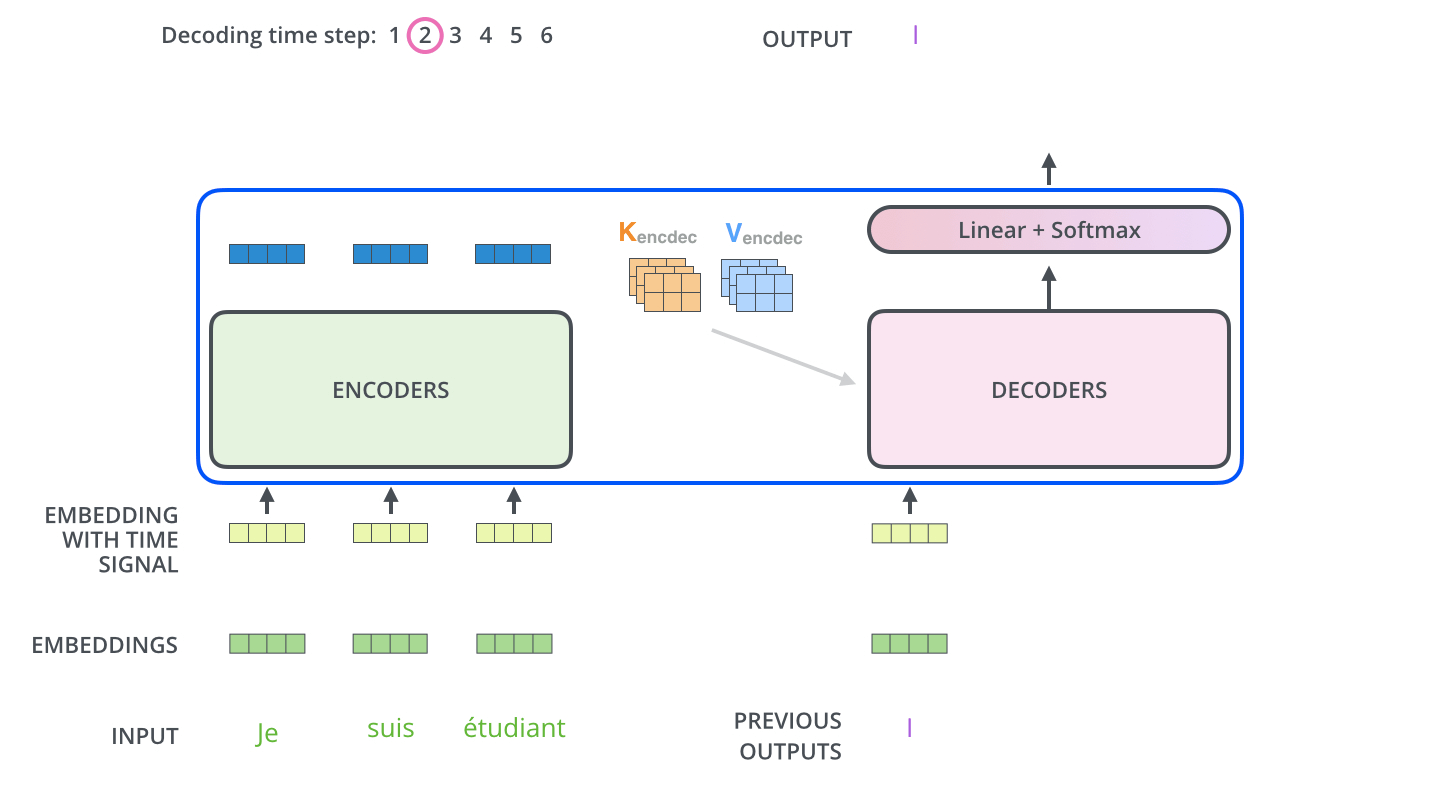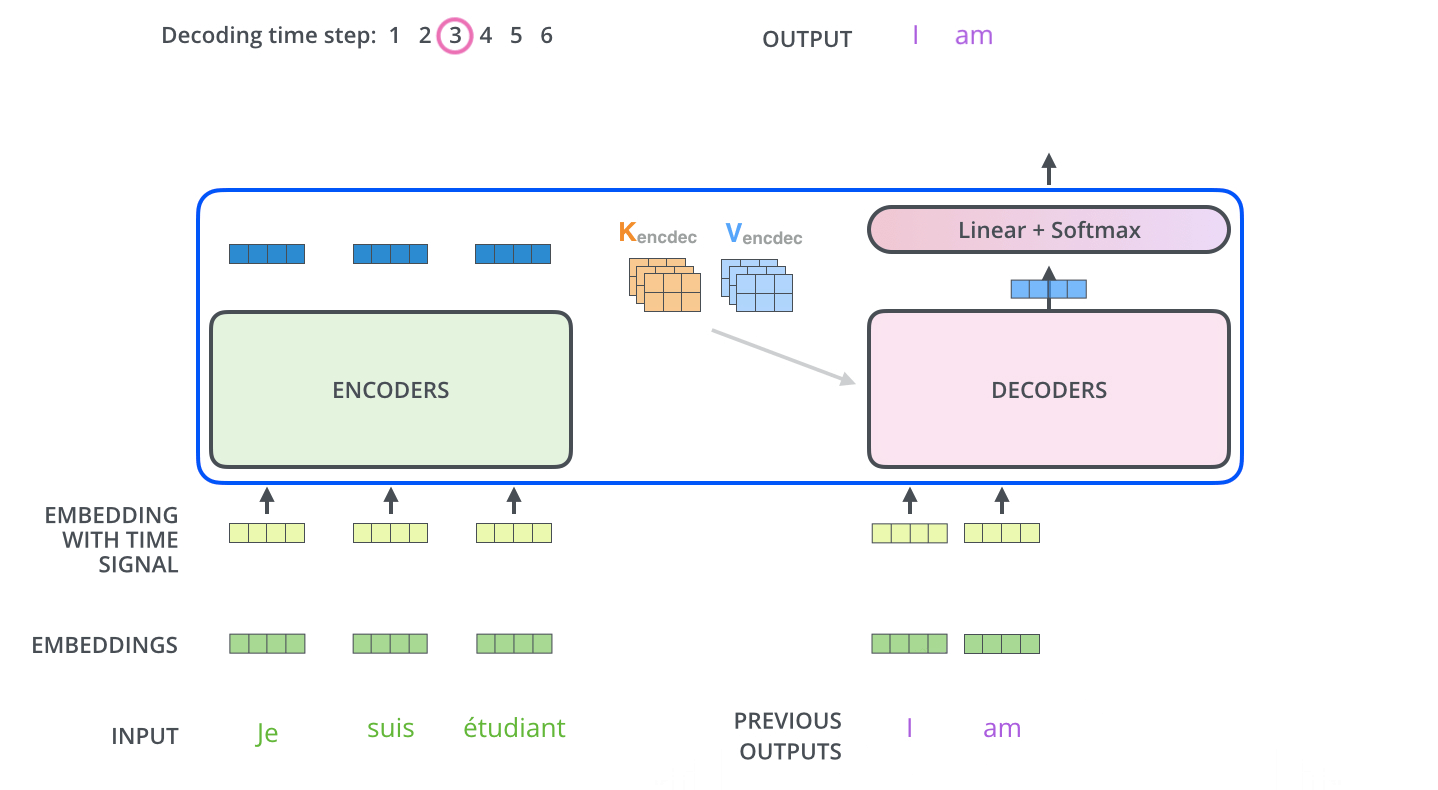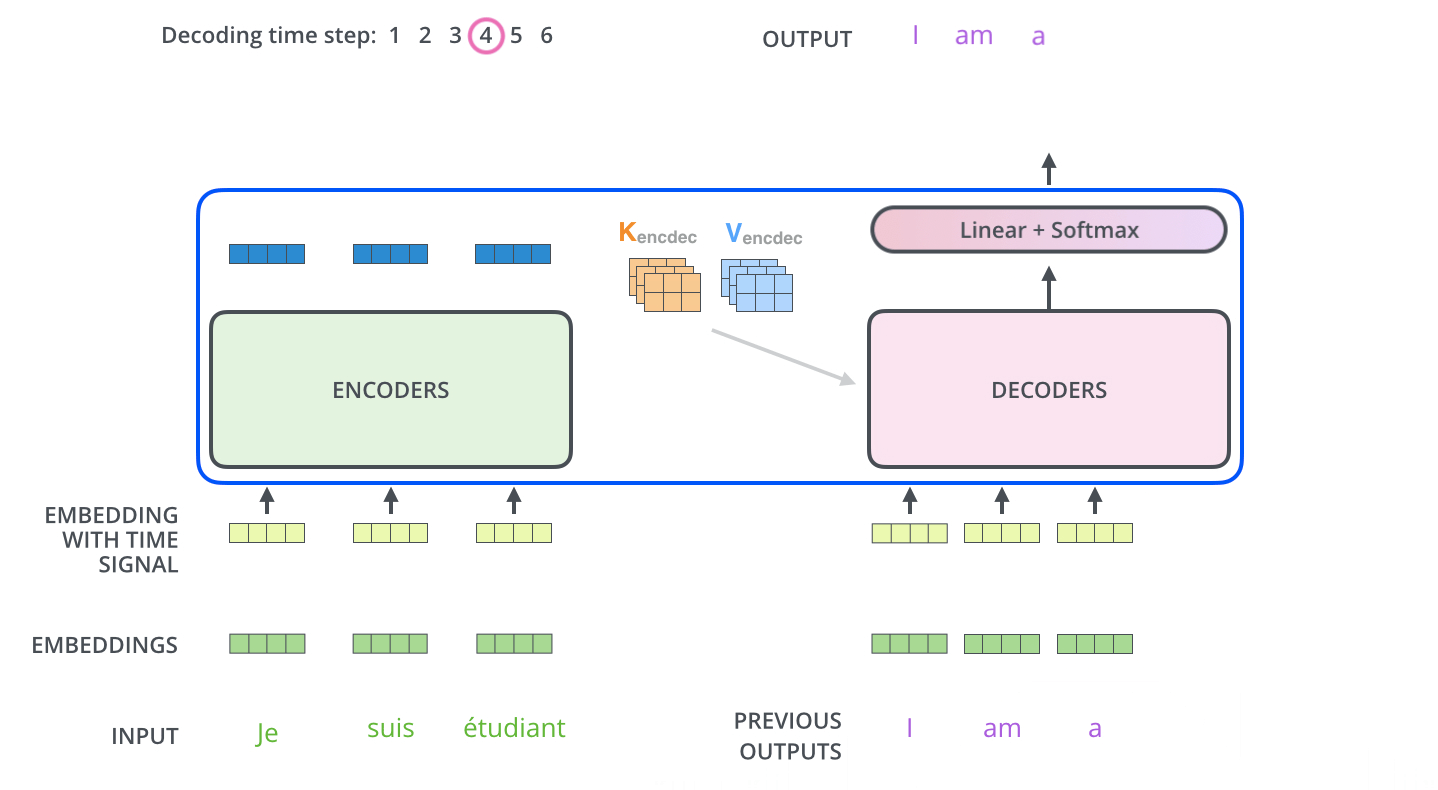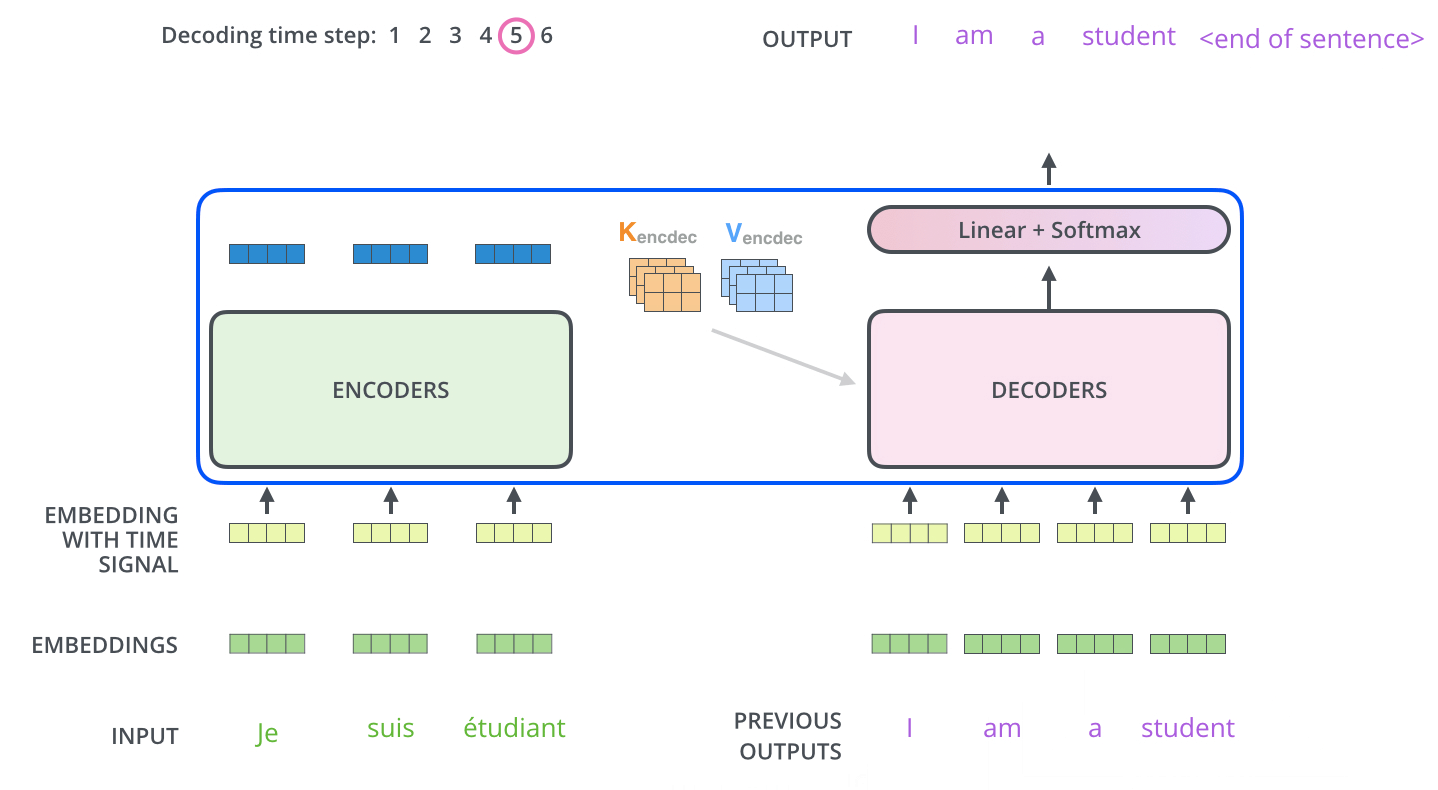
线性层与Softmax
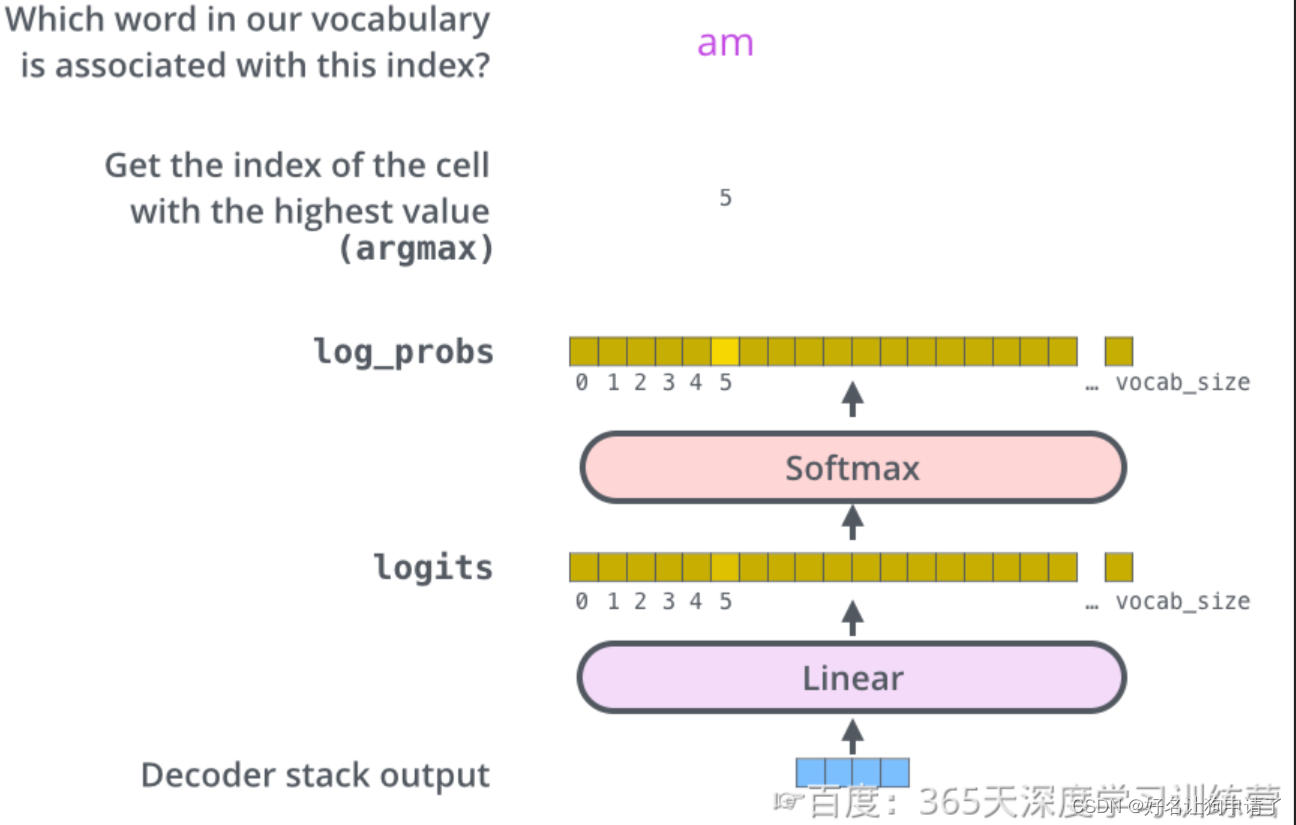
解码器的最终输出结果是一个向量,其中的每个元素都是浮点数。和基本的分类模型一样,通过线性层和Softmax层可以将向量转换为单词对应的概率(类似于不同的分类)。
线性层就是一个普通的全连接网络,它把解码器输出的向量,映射成一个更大的向量,这个向量被称为logits向量。假设我们的模型有10000个单词(词汇表的容量),此logits向量便要有10000维,每一个数表示一个单词的分数。
然后通过Softmax层把这些数字转换为概率(就是转换为全是正数,并且相加为1),这时我们就可以选择概率最高的那个数字对应的单词,作为本轮的输出单词。
损失函数
Transformer训练的时候,需要将解码器的输出和label一同送入损失函数,以获得Loss。通过前面的分析我们可以得知,损失函数只需要和分类网络一样使用交叉熵即可。通过损失函数的反向传播,修正模型的参数,最终得到目标模型。
总结与心得体会
本周在理论上学习了Transformer模型的结构、组成、训练过程。让我印象最深刻的就是Seq2Seq模型不仅有一个输入头,它的编码器是和CV模型共通的,但是编码器也有输入,并且先每个时间步只输出一个单词,这点和RNN一样并没有什么变化 。这也制约了NLP任务的训练和推理。另外我没想到它的损失函数竟然和最基础的分类网络一样,用简单的交叉熵损失就可以。