曲面上的曲线PCurve,字面上理解即为参数曲线(Parametric Curve)。在几何建模中,PCurve通常被描述为附加在参数曲面之间公共边上的数据结构。从更具体的定义来看,当给定一个曲面方程,并且其参数u和v是另一个参数t的函数时,通过将这些参数代入曲面方程,随着t的变化,我们就可以得到曲面上的一条单参数曲线,这就是曲面上的曲线或简称曲面上曲线(Curve on Surface)。
在Open CASCADE中,PCurve用于描述参数曲面的双参数空间中的二维样条曲线。所有的三维曲线(面的边界)都对应于二维参数曲线PCurve,二维参数曲线PCurve上的二维点对应实际曲线上的三维点。通过这种方法,可以方便地提取和处理曲面的边界和其他相关特性。
#include <Geom_Plane.hxx>
#include <gp_Ax3.hxx>
#include <Geom_RectangularTrimmedSurface.hxx>
#include <Geom_Geometry.hxx>
#include <BRepBuilderAPI_MakeFace.hxx>
#include <Precision.hxx>
#include <TopExp_Explorer.hxx>
#include <BRep_Tool.hxx>
#include <TopoDS.hxx>#include"Viewer.h"int main(int argc, char* argv[])
{gp_Ax3 loc;loc = gp_Ax3(gp_Pnt(0, 0, 0), gp_Dir(0, 0, 1), gp_Dir(1, 0, 0));Handle(Geom_Plane) C = new Geom_Plane(loc);Handle(Geom_Surface) S =new Geom_RectangularTrimmedSurface(C, -1, 1, -1, 1, Standard_True, Standard_True);TopoDS_Shape res= BRepBuilderAPI_MakeFace(S, Precision::Confusion());TopExp_Explorer ex(res, TopAbs_EDGE);Standard_Real f, l;res.Orientation(TopAbs_FORWARD);for (Standard_Integer i = 1; ex.More(); ex.Next(), i++) {Handle(Geom2d_Curve) c = BRep_Tool::CurveOnSurface(TopoDS::Edge(ex.Current()), TopoDS::Face(res), f, l);if (c.IsNull()) {std::cout << "Error: Edge " << i << " does not have pcurve" << std::endl;continue;}Standard_Real fr = c->FirstParameter(), lr = c->LastParameter();Standard_Boolean IsPeriodic = c->IsPeriodic();std::cout << "No." << i << ":" << "FirstParameter=" << f<<" " << "LastParameter=" << l << " " << "IsPeriodic=" << IsPeriodic << " " << std::endl;}Viewer vout(50, 50, 500, 500);vout << res;vout.StartMessageLoop();return 0;
}
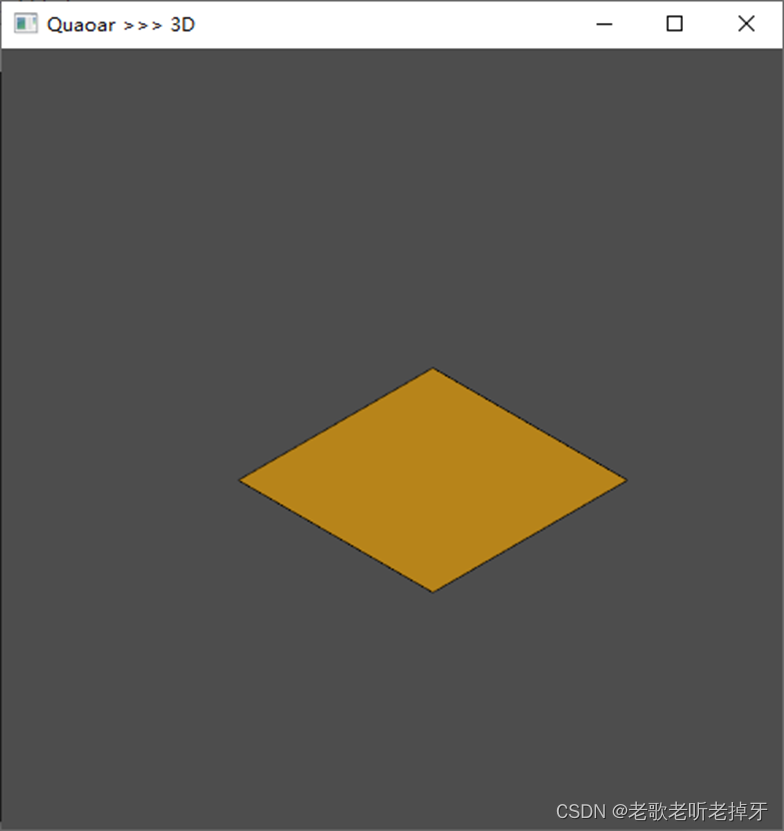
No.1:FirstParameter=-1 LastParameter=1 IsPeriodic=0
No.2:FirstParameter=-1 LastParameter=1 IsPeriodic=0
No.3:FirstParameter=-1 LastParameter=1 IsPeriodic=0
No.4:FirstParameter=-1 LastParameter=1 IsPeriodic=0