个人主页:学习前端的小z
个人专栏:HTML5和CSS3悦读
本专栏旨在分享记录每日学习的前端知识和学习笔记的归纳总结,欢迎大家在评论区交流讨论!
文章目录
- ✍一、MATLAB数据类型和运算符
- 💎1 MATLAB的数据类型
- 🌹1.1 特殊常量
- 🌹1.2 变量
- 🌹1.3 整数
- 🌹1.4 浮点数
- 🌹1.5 复数
- 💎2 MATLAB运算符
- 🌹2.1 算术运算符
- 🌹2.2 关系运算符
- 🌹2.3 逻辑运算符
- 🌹2.4 优先级
- ✍二、矩阵的创建
- 💎1 直接输入矩阵
- 💎2 冒号生成矩阵
- 💎3 利用函数生成矩阵
- 🌹3.1 linspace函数
- 🌹3.2 logspace函数
- 💎4 利用文本文件生成矩阵
- 💎5 利用M文件生成矩阵
- 💎6 特殊矩阵的生成
- 🌹6.1 单位矩阵
- 🌹6.2 0矩阵
- 🌹6.3 1矩阵
- 🌹6.4 魔方矩阵
- 🌹6.5 0~1均匀分布随机矩阵
- 🌹6.6 正态分布随机矩阵
- 🌹6.7 对角矩阵
- 🌹6.8 三角矩阵
✍一、MATLAB数据类型和运算符
💎1 MATLAB的数据类型
🌹1.1 特殊常量
MATLAB有些固定的变量,称为特殊常量。这些特殊常量具有特定的意义,用户在定义变量名时应避免使用。
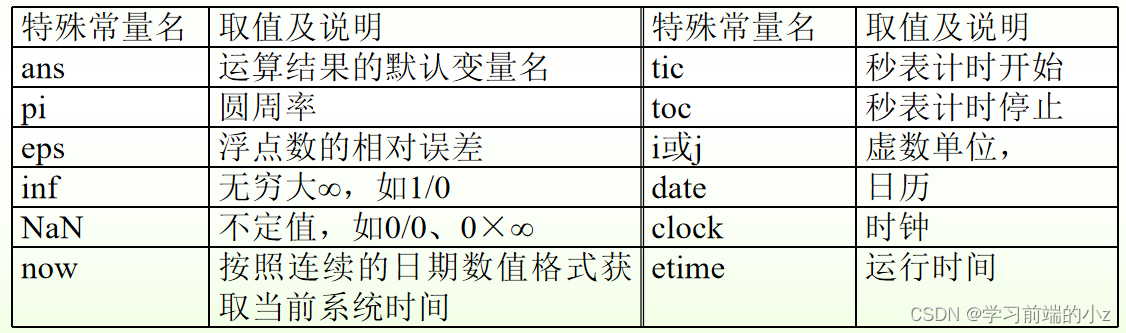
在MATLAB语言中,需要知道程序或者代码的运行时间,可以使用计时函数tic/toc,和etime两种方法实现。
(1)tic/toc方法
例如:
tic
%程序段
toc%返回时间就是程序运行时间
(2)etime方法
函数命令格式为:
etime(t2,t1)
其中t2和t1可以使用clock函数获得。
例如:
t1=clock
%程序段
🌹1.2 变量
变量是其值可以改变的量,是数值计算的基本单元。MATLAB变量使用无需事先定义和声明,也不需要指定变量的数据类型。可以自动根据变量值或对变量操作来识别变量类型。在变量赋值过程中,自动使用新值替换旧值,用新值类型替换旧值类型。
变量的命名规则:
(1)变量名由字母、数字和下划线组成,且第一个字符为字母,不能有空格和标点符号。例如:“1a”,“a 1”、“_a”“a%”、“b-1”和“变量a”都是不合法的变量名。
(2)变量名区分大小写。例如P1Q,p1q,P1q,p1Q是四个不同的变量。
(3)变量名的长度上限为63个字符,第63个字符后面的字符被忽略。
(4)关键字或者系统的函数名。
🌹1.3 整数
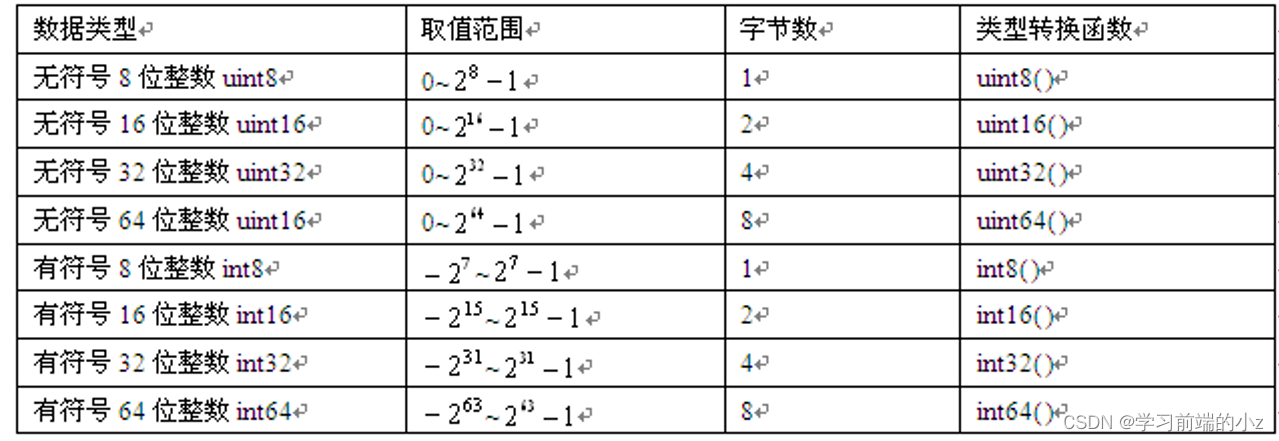
MATLAB R2020a提供8种常见的整数类型,可以使用类型转换函数将各种整数类型强制互相转换。下表给出MATLAB各种整数类型的取值范围和类型转换函数。
🌹1.4 浮点数
浮点数包括单精度型(single)和双精度型(double),默认的数据类型是双精度型。单精度型取值范围是
;双精度型取值范围是 ,浮点数类型可以用类型转换函数single ( )和double()互相转换。
>> y1=int8(1.6e16) %将浮点数强制转换为有符号8位整数
y1 = 127
>> y2=int16(1.6e16) %将浮点数强制转换为有符号16位整数
y2= 32767
>> y3=int8(2.65) % 将浮点数强制转换为有符号8位整数
y3 = 3
>> y4=uint8(-3.2) % 8位无符号整数最小值是0
y4 = 0
>> y5=1/3 % MATLAB默认的数据类型是双精度型
y5 = 0.3333
>> y6=single(1/3) % 用single()函数,将双精度型强制转换为单精度型
y6 = 0.3333
🌹1.5 复数
MATLAB用特殊变量i或j表示虚数的单位。MATLAB中复数运算可以直接进行。复数z可以通过以下几种方式产生:
z=a+bi或者z=a+bj %其中a为实部,b为虚部
z=a+bi或者z=a+bj
z=rexp(ithetha) %其中r为半径,thetha为相角(以弧度为单位)
z=complex(a,b)
z=a+b*sqrt(-1)
MATLAB复数运算常见函数如下表所示:
💎2 MATLAB运算符
三种常见运算符:算术运算符、关系运算符和逻辑运算符
🌹2.1 算术运算符
(1)加、减、乘和乘方运算规则与传统的数学定义一样,用法也相同。
(2)点运算是指对应元素点对点运算,要求参与运算矩阵的维度要一样。点左除与点右除不一样,A./B是指A的对应元素除以B的对应元素,A.\B是指B的对应元素除以A的对应元素。
(3)MATLAB除法相对复杂些,对于单个数值运算,右除和传统除法一样,即a/b=a÷b;而左除与传统除法相反,即a\b=b÷a。对于矩阵运算,左除A\B相当于矩阵方程组 的解,即X=A\B=inv(A)B; 右除B/A相当于矩阵方程组 的解,即X=B/A= Binv(A)。
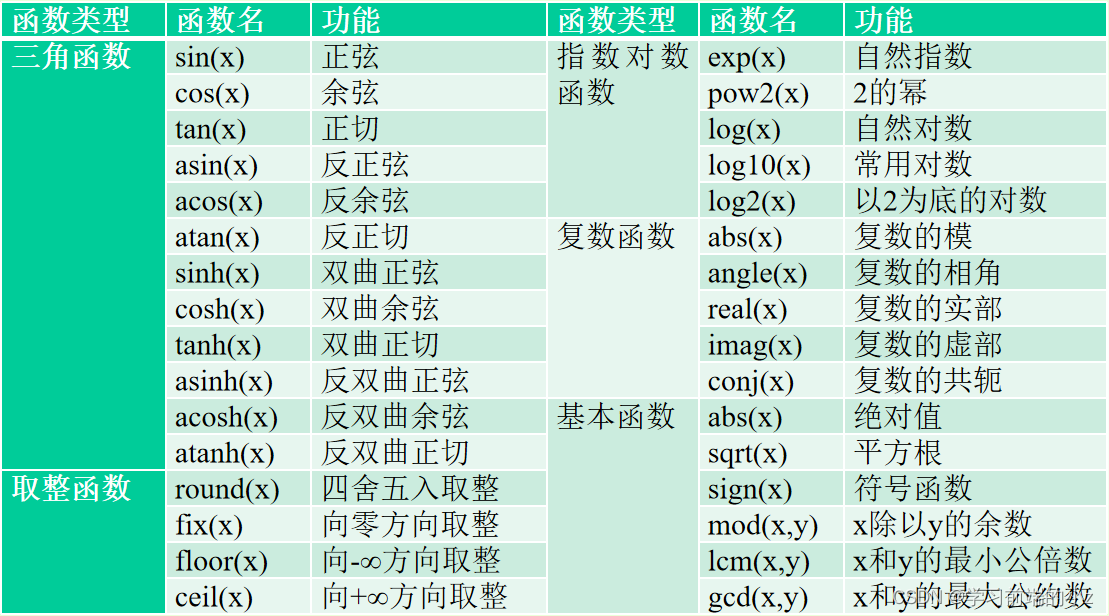
下图是MATLAB中常用的数学函数:
说明:
(1)abs函数可以求实数的绝对值,复数的模和字符串的ASII值,比如:abs(-2.3)=2.3;abs(3+4i)=5; abs(‘a’)=97。
(2)MATLAB语言有四个取整的函数:round,fix,floor和ceil,它们之间是有区别的。比如:round(1.49)=1;fix(1.49)=1;floor(1.49)=1;ceil(1.49)=2。round(-1.51)=-2;fix(-1.51)=-1;floor(-1.51)=-2;ceil(-1.51)=-1。
(3)MATLAB语言中以自然对数函数是log10(x),而不是lg(x),自然对数函数是exp(x),而不是e^(x)。
(4)符号函数sign(x)的值有三种,当x=0,sign(x)=0;当x>0, sign(x)=1;当x<0, sign(x)=-1。
(5)MATLAB语言三角函数都是对弧度操作,使用三角函数时候,需要将度变换为弧度,变换公式为:弧度=2pi(度/360)。比如:数学上的sin(60),MATLAB语言应该写成:sin(2pi60/360)。
🌹2.2 关系运算符
MATLAB语言有大于、大于等于、小于、小于等于、等于和不等于六种常见关系运算符,如下表所示:
注意:关系运算符主要用于数与数、数与矩阵元素、矩阵与矩阵之间元素进行比较,返回两者之间的关系的矩阵(由数0和1组成),0和1分别表示关系不满足和满足。矩阵与矩阵之间进行比较时,两个矩阵的维度要一样。
🌹2.3 逻辑运算符
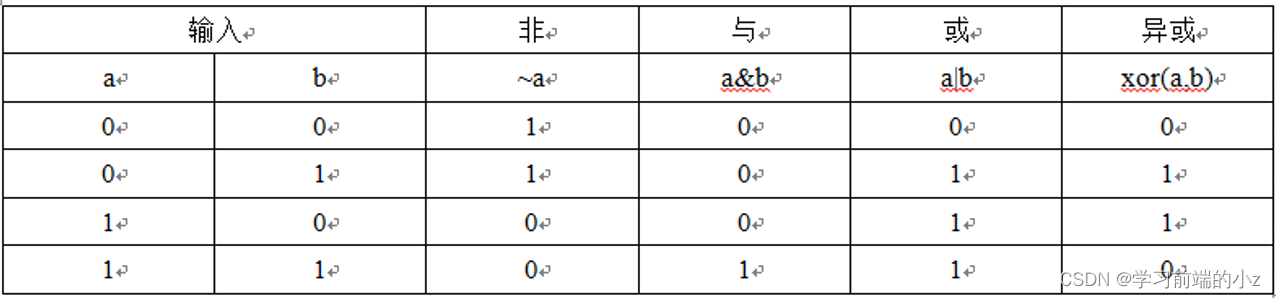
4种逻辑运算符:&(与)、|(或)、~(非)和xor(异或)。
运算规则:
(1)在逻辑运算中,所有非零元素均被认为真,用1表示;零元素为假,用0表示。
(2)如果两个同维矩阵参与逻辑运算,矩阵对应元素按标量规则进行逻辑运算,得到同维的由1或者0构成的矩阵。
(3)如果一个标量和一个矩阵参与逻辑运算,标量和矩阵的每个元素按标量规则进行逻辑运算,得到同维的由1或者0构成的矩阵。
🌹2.4 优先级
算术运算符优先级最高,关系运算符次之,逻辑运算符为最低。即程序先执行算术运算,然后执行关系运算,最后执行逻辑运算。在逻辑“与”、“或”、“非”三种运算符中,“非”的优先级最高,“与”和“或”的优先级相同,即从左往右执行。实际应用中,可以通过括号来调整运算的顺序。
例如:
>> q=(1>2|2<1+2)
q = 1
其中,MATLAB先执行算术运算:1+2=3,然后执行关系运算1>2为0,和2<3为1,最后执行逻辑运算0|1=1。
个人主页:学习前端的小z
个人专栏:HTML5和CSS3悦读
本专栏旨在分享记录每日学习的前端知识和学习笔记的归纳总结,欢迎大家在评论区交流讨论!
文章目录
- ✍一、MATLAB数据类型和运算符
- 💎1 MATLAB的数据类型
- 🌹1.1 特殊常量
- 🌹1.2 变量
- 🌹1.3 整数
- 🌹1.4 浮点数
- 🌹1.5 复数
- 💎2 MATLAB运算符
- 🌹2.1 算术运算符
- 🌹2.2 关系运算符
- 🌹2.3 逻辑运算符
- 🌹2.4 优先级
- ✍二、矩阵的创建
- 💎1 直接输入矩阵
- 💎2 冒号生成矩阵
- 💎3 利用函数生成矩阵
- 🌹3.1 linspace函数
- 🌹3.2 logspace函数
- 💎4 利用文本文件生成矩阵
- 💎5 利用M文件生成矩阵
- 💎6 特殊矩阵的生成
- 🌹6.1 单位矩阵
- 🌹6.2 0矩阵
- 🌹6.3 1矩阵
- 🌹6.4 魔方矩阵
- 🌹6.5 0~1均匀分布随机矩阵
- 🌹6.6 正态分布随机矩阵
- 🌹6.7 对角矩阵
- 🌹6.8 三角矩阵
✍二、矩阵的创建
MATLAB各种数据类型都是以矩阵形式存在,大部分运算都是基于矩阵运算,矩阵主要分为三类:数值矩阵,符号矩阵和特殊矩阵
💎1 直接输入矩阵
MATLAB语言最简单的创建矩阵方法是通过键盘在命令窗口直接输入矩阵,直接输入法的规则是:
- 将所有矩阵元素置于一对方括号“[ ]”内;
- 同一行不同元素之间用逗号“,”或者空格符来分隔;
- 不同行用分号“;”或者回车符分隔。
例如:
在命令空间输入:
>> A=[1 2;3 4] %元素之间用空格符分隔,换行用分号A =1 2
3 4
MATLAB语言创建复数矩阵,方法和创建一般实数矩阵一样,虚数单位用i或者j表示。
- 虚部和虚数单位之间可以使用乘号“”连接,也可以忽略乘号“”;
- 复数矩阵元素可以用运算表达式;
- 虚数单位用i或者j,显示时都是i。
例如,创建复数矩阵:
>> B=[1+2i,2-3*j;2+2*sqrt(-2),3.5j]
B =1.0000 + 2.0000i 2.0000 - 3.0000i2.0000 + 2.8284i 0.0000 + 3.5000i
💎2 冒号生成矩阵
利用冒号“:” 产生步长相等的一维数组或行向量。其格式为:
x=a:step:b
- a是数组或者行向量的第一个元素,b是最后一个元素,step是步长增量;
- 冒号表达式可以产生一个由a开始到b结束,以步长step自增或自减(步长为负值,b<a)的数组或者- 行向量;
- 如果步长step=1,则冒号表达式可以省略步长,直接写为x=a:b。
例如:
>> x1=1:1:10
x1 = 1 2 3 4 5 6 7 8 9 10
>> x2=1:10
x2 = 1 2 3 4 5 6 7 8 9 10
>> x3=10:-2:0
x3 = 10 8 6 4 2 0
💎3 利用函数生成矩阵
🌹3.1 linspace函数
可以用linspace函数生成初值、终值和元素个数已知的一维数组或者行向量,元素之间是等差数列。其调用格式如下:
x=linspace(a,b,n)
- a和b分别是生成一维数组或者行向量的初值和终值,n是元素总数。当n省略时候,自动产生100个元素;
- linspace函数产生的一维数组或者行向量,n个元素是等差数列;
- 当a>b,元素之间是等差递减;当a<b,元素之间是等差递增;
- 显然,linspace(a,b,n)与a: (b-a)/(n-1): b是等价的。
例如:
>> x1=linspace(0,10,5)
x1 = 0 2.5000 5.0000 7.5000 10.0000
>> x2=linspace(10,0,5)
x2 = 10.0000 7.5000 5.0000 2.5000 0
>> x3=10:(0-10)/(5-1):0
x3 =10.0000 7.5000 5.0000 2.5000 0
🌹3.2 logspace函数
MATLAB语言可以用logspace函数生成一维数组或者行向量,元素之间也是对数等比数列。其调用格式如下.
x=logspace(a,b,n)
其中:
- 第一个元素为10a,最后一个元素为10b,元素个数为n的对数等比数列;
- 如果b的值为pi,则该函数产生到pi之间n个对数等比数列。
例如:
>> x1=logspace(1,2,10)
x1 = 10.0000 12.9155 16.6810 21.5443 27.8256 35.9381 46.4159 59.9484 77.4264 100.0000
>> x2=logspace(1,pi,10)
x2 = 10.0000 8.7928 7.7314 6.7980 5.9774 5.2558 4.6213 4.0634 3.5729 3.1416
💎4 利用文本文件生成矩阵
矩阵还可以由文本文件生成,即先建立txt数据文件,然后在命令窗口直接调用该文件,就能产生数据矩阵。需要注意,txt文件中不含变量名称,文件名为矩阵变量名,每行数值个数相等。
优点:可以将数据存储在文本文件中,利用load函数,直接将数据读入工作空间中,自动生成矩阵,而不需要手动输入数据。
例如:
利用文本文件建立矩阵A,其中
把下面代码另存为工作目录中,文件名为A.txt文件。
1 2
3 4
>> load A.txt
>> A
A =1 23 4
💎5 利用M文件生成矩阵
对于一些比较大的常用矩阵,可以立一个M文件,在命令窗口中调用文件,适合大型矩阵创建,便于修改。需要注意,M文件中的矩阵变量名不能与文件名相同,否则变量名和文件名会混乱。
例如:
%定义exam_2_2.m函数,将下面代码另存为工作目录下的
A=[34 32 30 28 26 24
32 30 28 26 24 22
30 28 26 24 22 20
28 26 24 22 20 18
26 24 22 20 18 16]
>> exam_2_2
A = 34 32 30 28 26 2432 30 28 26 24 2230 28 26 24 22 2028 26 24 22 20 1826 24 22 20 18 16
💎6 特殊矩阵的生成
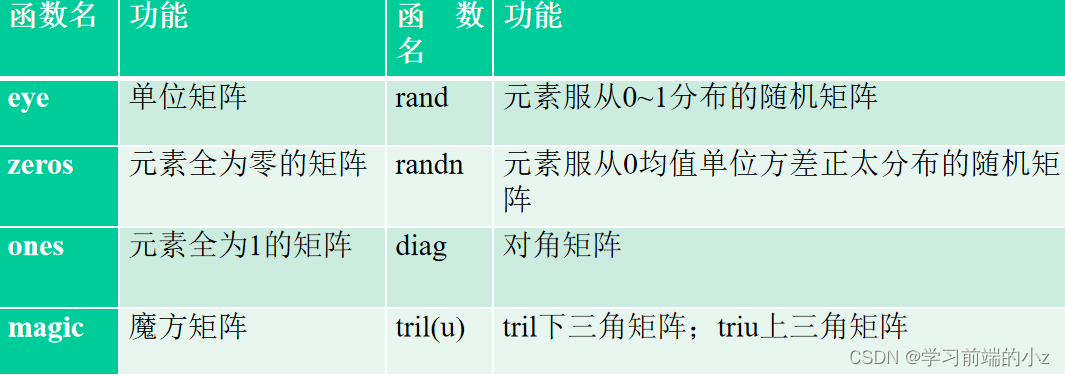
MATLAB语言中内置了许多特殊矩阵的生成函数,可以通过这些函数自动生成具有不同特殊性质的矩阵。下表是MATLAB语言常见特殊矩阵函数。
🌹6.1 单位矩阵
MATLAB语言生成单位矩阵的函数是eye,其调用格式如下:
A1=eye(n);
A2=eye(m,n)。
其中:
A1=eye(n)表示生成n行n列的单位矩阵;
A2=eye(m,n)表示生成m行n列的单位矩阵。
例如:
>> A1=eye(3)
A1= 1 0 00 1 00 0 1
>> A2=eye(2,3)
A2 =1 0 00 1 0
🌹6.2 0矩阵
MATLAB语言生成所有元素为0的矩阵函数是zeros,其调用格式如下:
A1=zeros(n);
A2=zeros(m,n)。
其中:
A1= zeros(n)表示生成n行n列的0矩阵;
A2=zeros(m,n)表示生成m行n列的0矩阵。
例如:
>> A1=zeros(3)
A1 = 0 0 00 0 00 0 0
>> A2=zeros(1,3)
A 2= 0 0 0
🌹6.3 1矩阵
MATLAB语言生成所有元素为1的矩阵函数是ones,其调用格式如下:
A1=ones(n);
A2=ones(m,n)。
其中:
- A1= ones(n)表示生成n行n列的1矩阵;
- A2=ones(m,n)表示生成m行n列的1矩阵。
例如:
>> A1=ones(3)
A1= 1 1 11 1 11 1 1
>> A2=ones(2,3)
A2 =1 1 11 1 1
🌹6.4 魔方矩阵
魔方矩阵是指行、列、正和反斜对角线元素之和都相等的矩阵,MATLAB语言用magic函数生成魔方矩阵,其调用格式如下:
A=magic(n)
其中,A=magic(n)表示生成n行n列的魔方矩阵,n>0且n≠2 。
例如:
>> A=magic(3)
A = 8 1 63 5 74 9 2
>> B=sum(A) %计算每列的和
B = 15 15 15
>> C=sum(A') %计算每行的和
C = 15 15 15
显然,由B和C结果可知,矩阵A是一个魔方矩阵。
🌹6.5 0~1均匀分布随机矩阵
MATLAB语言生成0~1均匀分布的随机矩阵函数是rand,其调用格式如下:
- A1= rand(n)表示生成 n*n个元素值为0~1均匀分布的随机矩阵;
- A2= rand(m, n)表示生成m*n 个元素值为0~1均匀分布的随机矩阵;
- A3=a+(b-a)rand(m,n) 表示生成mn 个元素值为a~b均匀分布的随机矩阵。
例如:
>> A1=rand(3)
A1 = 0.8147 0.9134 0.27850.9058 0.6324 0.54690.1270 0.0975 0.9575
>> A3 = 10 + (15 - 10)*rand(2,3)
A3 = 10.7094 14.5787 14.797512.1088 13.9610 13.2787
🌹6.6 正态分布随机矩阵
MATLAB语言生成均值为0,单位方差的正态分布的随机矩阵函数是randn,其调用格式如下:
- A1= randn(n)表示生成 n*n个元素且均值为0,单位方差的正态分布的随机矩阵;
- A2= randn(m, n)表示生成m*n 个元素的正态分布随机矩阵;
- A3=a+sqrt(b)*randn(m,n) 表示均值为a,方差为b。
例如:
>> A1=randn(3)
A1 = -1.2075 0.4889 -0.30340.7172 1.0347 0.29391.6302 0.7269 -0.7873
>> A3 = 1 + sqrt(0.1)*randn(2,3) % 均值为1,方差为0.1
A3 =1.1028 1.4333 0.96770.7613 0.4588 0.9236
🌹6.7 对角矩阵
MATLAB语言生成对角矩阵函数是diag,其调用格式如下:
A=diag(v,k)表示生成以向量v元素作为矩阵A的第k条对角线元素的对角矩阵。
当k=0时,v 为A的主对角线;当k>0时,为主对角线上方第k条对角线元素;当k<0时,为主对角线下方第k条对角线元素。
例如:
>> v=[3 2 1];
>> A1=diag(v)
A1 = 3 0 00 2 00 0 1
>> A2=diag(v,1)
A2 = 0 3 0 00 0 2 00 0 0 10 0 0 0
若A是一个矩阵,则diag(A)是提取矩阵A的对角线矩阵。
>> A=[1 2 3;4 5 6];
>> B=diag(A)
B = 15
🌹6.8 三角矩阵
MATLAB语言生成三角矩阵函数是tril和triu,其调用格式如下:
- A1=tril(A,k)表示生成矩阵A中第k条对角线的下三角部分的矩阵;
- A1=triu(A,k)表示生成矩阵A中第k条对角线的上三角部分的矩阵;
其中, k=0为A的主对角线,k>0为A的主对角线以上, k<0为A的主对角线以下。
例如:
>> A=ones(4);
>> L=tril(A,-2)
L =0 0 0 00 0 0 01 0 0 01 1 0 0
>> U=triu(A,0)
U =1 1 1 10 1 1 10 0 1 10 0 0 1