公众号:编程驿站











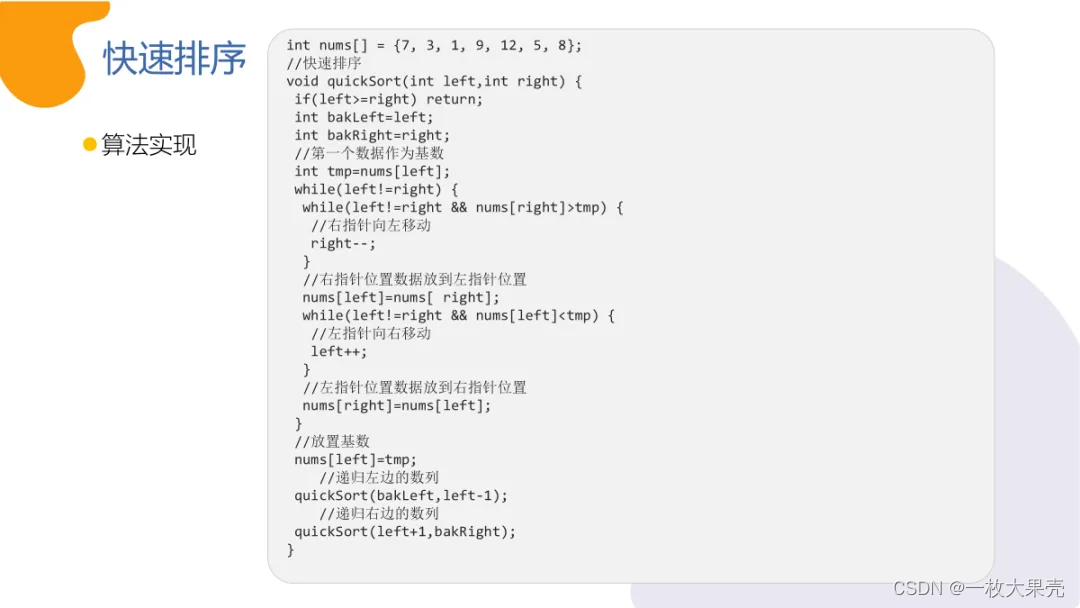


综合练习:
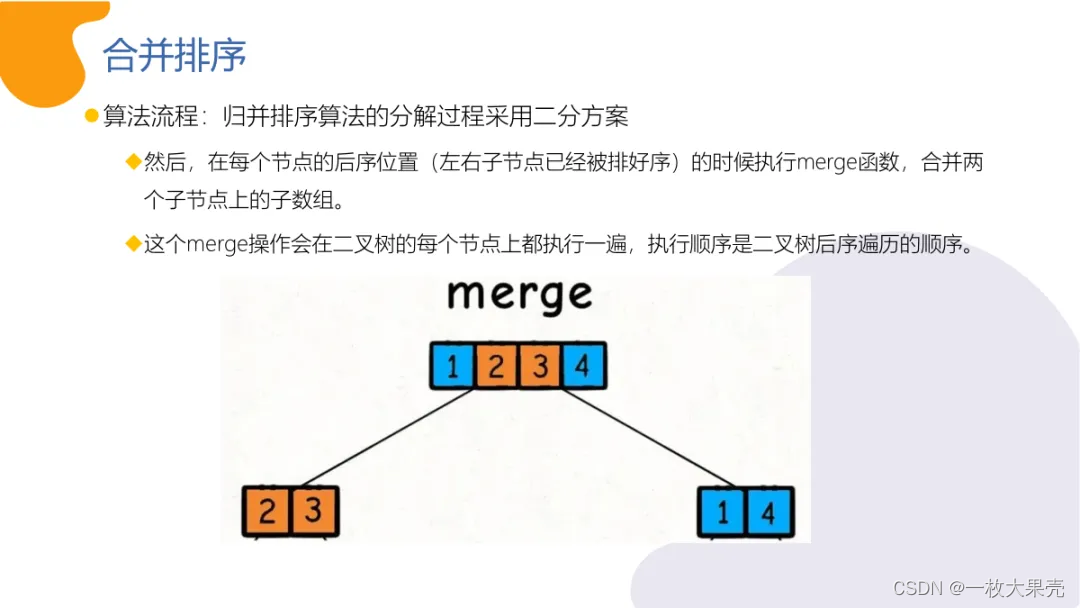
分治算法很有哲学蕴味:老祖宗所言 合久必分,分久必合,分开地目的是为了更好的合并。分治算法的求解流程:分解问题:将一个需要解决的、看起很复杂 原始问题 分拆成很多独立的子问题,子问题与原始问题有相似性。求解子问题:子问题除了与原始问题具有相似性,也具有独立性,即所有子问题都可以独立求解。合并子问题: 合并每一个子问题的求解结果最终可以得到原始问题的解。
适用情况:
1.该问题的规模缩小到一定的程度就可以容易地解决;
2.该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质;
3.利用该问题分解出的子问题的解可以合并为该问题的解;
4.该问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子子问题。
一、整数划分问题。给你一个数,问你所有的划分方式,比如4,4=1+3,4=1+1+2,4=2+2,4=1+1+1+1。我们来分析一下,我们想用分治的话,就要找子问题,假设n是要划分的数,m说最大的加数,n=4,m=3。分解成两类的子问题,一个是:一个是有m的情况,一个是没有m的情况,然后将有m的情况继续划分,分解成有m-1和没有m-1的情况,一直划分下去,直到m=1。比如n=4,m=3,划分成的子问题:有3,无3,有2,无2,有1,无1(没有意义,除非0+4=4),将这些子问题合并起来大问题就解决了。二、求最大连续和。给出一个长度为n的序列A1,A2,A3·····An,求最大连续和。如序列(6,-1 , 5, 4,-7), 该序列中的最大和是6 +( - 1)+ 5 + 4 = 14。基本思路是使用枚举法,三重嵌套循环,时间复杂度为n的三次方。我们来用分治法解决这个问题。1.划分问题:将序列分成元素个数尽可能相等的两半。2.递归求解:分别求出位于左半和右半的最佳序列。3.合并问题:求出起点位于左半,终点位于右半的最大连续和序列,和子问题最优解比较。