有限差分法求解一维、二维波动方程-编程知识

有限差分法求解一维、二维波动方程

差分格式方法是数值计算方法中微分以及偏微分导数的一种离散化方法。具体来说，它使用相邻两个或者多个数值点的差分来取代偏微分方程中的导数或偏导数。选择差分格式是离散化偏微分方程的第一步，通过这种离散化，我们可以将连续空间区域上的问题转化为在离散网格点上进行计算，从而更容易在计算机上实现数值求解。

差分格式方法有多种，如显式与隐式算法。显式算法相对简单，但有时为了满足计算稳定的条件，需要取很小的步长，这可能导致计算时间大大增加。而隐式格式的求解过程可以取较大的步长，虽然求解过程较为复杂，但最后一定收敛。在实际应用中，根据问题的具体特性和求解要求，可以选择合适的差分格式方法。

一维波动方程可以表示为：

∂²u/∂t² = c² * ∂²u/∂x²

其中，u 是波函数，c 是波速，t 是时间，x 是空间坐标。

为了使用中心差分格式来离散化这个方程，我们需要对时间和空间导数都使用中心差分近似。对于时间二阶导数 ∂²u/∂t²，我们可以使用以下中心差分格式：

∂²u/∂t² ≈ $(u(t_{n+1}, x_i) - 2u(t_n, x_i) + u(t_{n-1}, x_i)) / dt^2$

对于空间二阶导数 ∂²u/∂x²，我们使用之前提到的中心差分格式：

∂²u/∂x² ≈ $(u(t_n, x_{i+1}) - 2u(t_n, x_i) + u(t_n, x_{i-1})) / dx^2$

将这两个差分格式代入波动方程，我们得到：

$(u(t_{n+1}, x_i) - 2u(t_n, x_i) + u(t_{n-1}, x_i)) / dt^2$ = $c² * (u(t_n, x_{i+1}) - 2u(t_n, x_i) + u(t_n, x_{i-1})) / dx^2$

整理上式，我们得到中心差分格式的有限差分方程：

$u(t_{n+1}, x_i)$ =

$2u(t_n, x_i) - u(t_{n-1}, x_i) + c² * dt^2 / dx^2 * (u(t_n, x_{i+1}) - 2u(t_n, x_i) + u(t_n, x_{i-1}))$

这个方程用于更新每个内部网格点的时间下一层的值。需要注意的是，由于中心差分格式涉及到三个时间层的值（ $t_{n-1}, t_n, t_{n+1}$ ），因此在时间迭代的开始，我们需要至少知道两个时间层的值（例如，通过初始条件和第一个时间步的计算）。

此外，中心差分格式通常需要满足一定的稳定性条件，这通常涉及到时间步长 dt 和空间步长 dx 的关系。对于一维波动方程，稳定性条件通常要求 dt 必须小于某个与 dx 和波速 c 相关的临界值。如果不满足稳定性条件，数值解可能会出现振荡或发散。

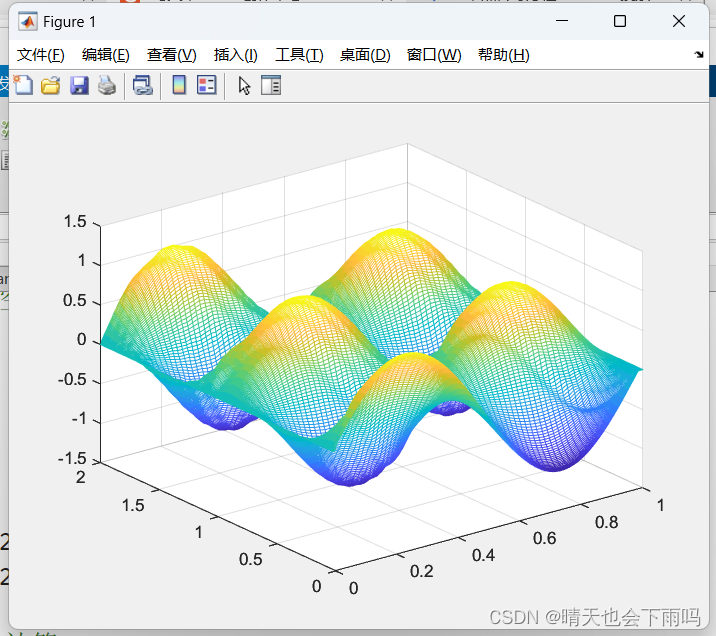
接着我们利用MATLAB差分方法求解下列一维波动方程：

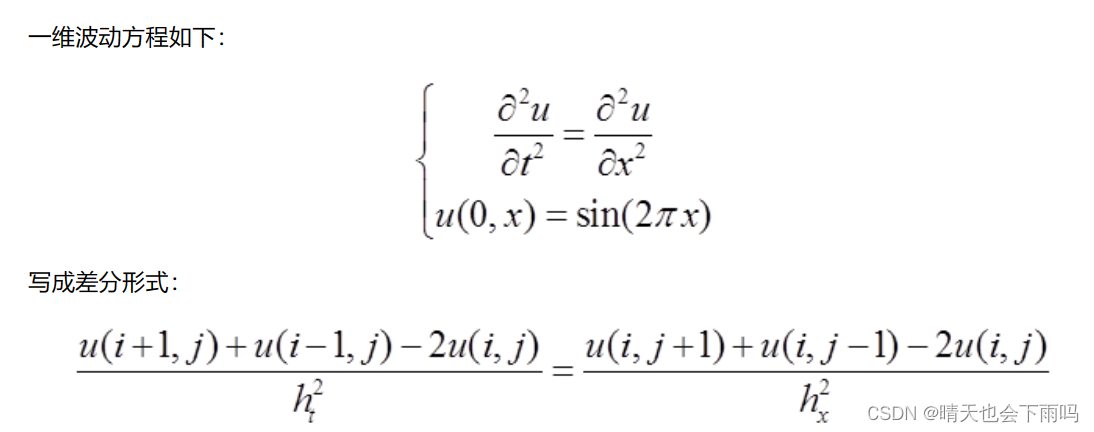
clear all;close all;clc;t = 2;          %时间范围，计算到2秒
x = 1;          %空间范围，0-1米
m = 320;        %时间方向分320个格子
n = 64;         %空间方向分64个格子
ht = t/(m-1);   %时间步长dt
hx = x/(n-1);   %空间步长dxu = zeros(m,n);%设置边界条件
i=1:n-1;
xx = i*x/(n-1);
u(1,1:n-1) = sin(2*pi*xx);
u(2,1:n-1) = sin(2*pi*xx);%根据推导的差分公式计算
for i=2:m-1for j=2:n-1u(i+1,j) = ht^2*(u(i,j+1)+u(i,j-1)-2*u(i,j))/hx^2 + 2*u(i,j)-u(i-1,j);end
end%画出数值解
[x1,t1] = meshgrid(0:hx:x,0:ht:t);
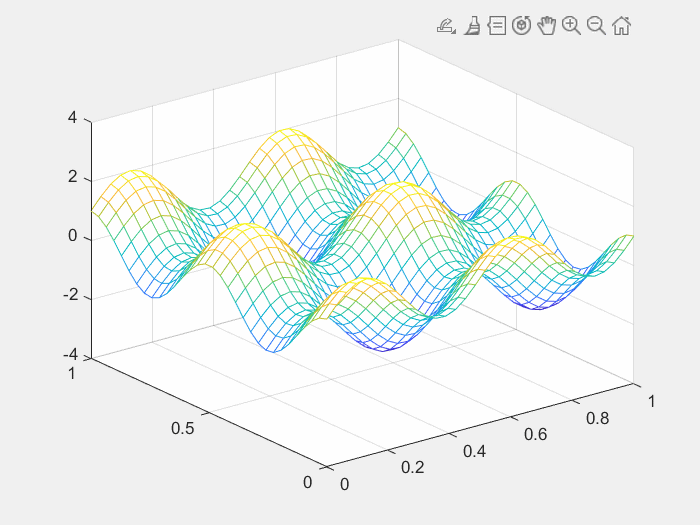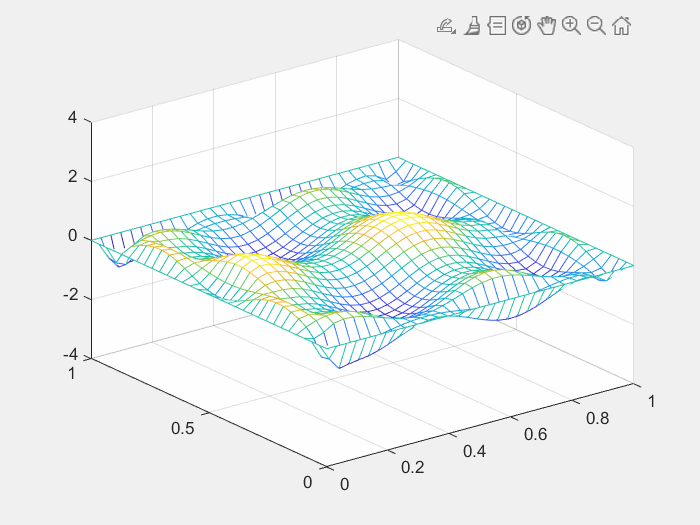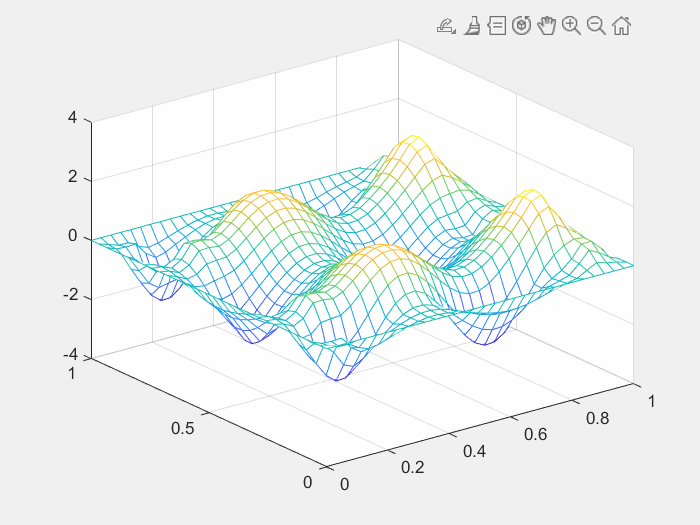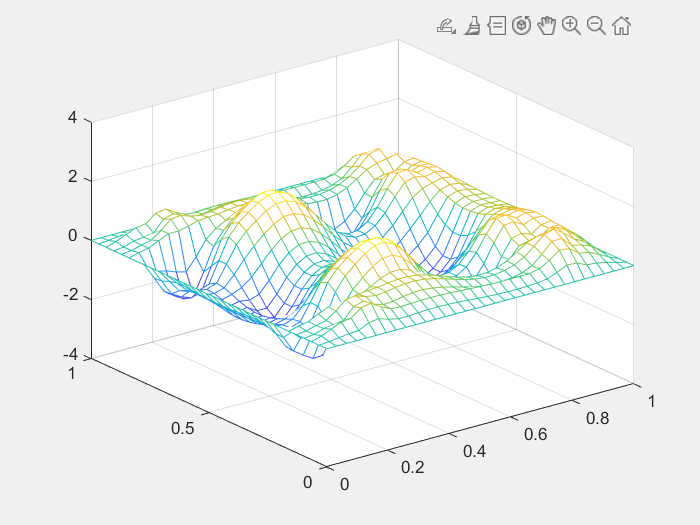
mesh(x1,t1,u)

运行结果如下图：

MATLAB差分方法求解下列二维波动方程：

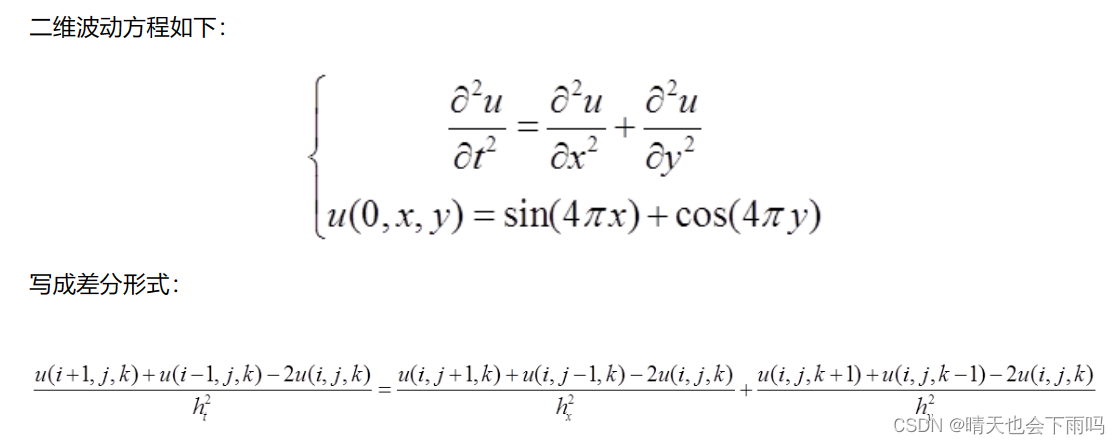
clear all;close all;clc;t = 3;          %时间范围，计算到3秒
x = 1;y = 1;    %空间范围，0-1米
m = 320;        %时间t方向分320个格子
n = 32;         %空间x方向分32个格子
k = 32;         %空间y方向分32个格子
ht = t/(m-1);   %时间步长dt
hx = x/(n-1);   %空间步长dx
hy = y/(k-1);   %空间步长dyu = zeros(m,n,k);%设置边界
[x,y] = meshgrid(0:hx:1,0:hy:1);
u(1,:,:) = sin(4*pi*x)+cos(4*pi*y);
u(2,:,:) = sin(4*pi*x)+cos(4*pi*y);%按照公式进行差分
for ii=2:m-1for jj=2:n-1for kk=2:k-1u(ii+1,jj,kk) = ht^2*(u(ii,jj+1,kk)+u(ii,jj-1,kk)-2*u(ii,jj,kk))/hx^2 + ...ht^2*(u(ii,jj,kk+1)+u(ii,jj,kk-1)-2*u(ii,jj,kk))/hy^2 + 2*u(ii,jj,kk) - u(ii-1,jj,kk);endend
endfor i=1:320figure(1);mesh(x,y,reshape(u(i,:,:),[n k]));axis([0 1 0 1 -4 4]);drawnow;F=getframe(gcf);%捕获坐标区或图窗作为影片帧I=frame2im(F);%从单个影片帧 F 返回真彩色 (RGB) 图像[I,map]=rgb2ind(I,256); %将 RGB 图像转换为索引图像，i索引图像，map颜色图if i == 1imwrite(I,map,'test123.gif','gif','Loopcount',inf,'DelayTime',0.03);%将图像写入图形文件elseimwrite(I,map,'test123.gif','gif','WriteMode','append','DelayTime',0.03);    end
end

运行结果如下图：