题目

链接：快乐数

题目解析

根据题目 试着画图找一下规律

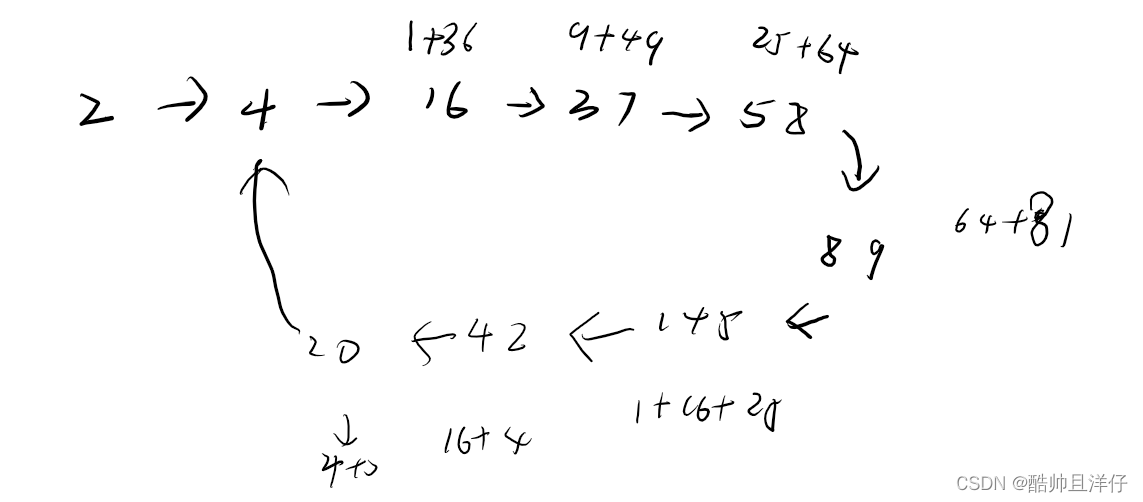
在这个题目中 只有两种情况

• 最后进入循环 没有1
• 或者进入循环 有1

鸽巢原理

看到这里肯定会有疑惑，为什么都会进入循环，难道就不会无限不循环吗，这里就要用一个知识来解释为什么一定会有循环了——“鸽巢原理”

• 鸽巢原理的简单形式：如果把 n+1个物品放入 n 个盒子中，那么至少有1个盒子包含有2个或更多的物品.（每个盒子必须不为空）

int的最大值

这里直接再给大一点直接999999999 那么由题目的要求，这算出来为9^2*10 也就是810
也就是int 在这变化的结果肯定实在[1,810]之间 ，那么再超过81次变化之后 一定会出现重复的数，也就是进入循环

算法原理

双指针 ——快慢指针

定义两个快慢指针 slow fast
快的指针走两步 ，慢的指针走一步
那么最终这两个指针会在进入循环后会相遇

如果相遇的位置为1，则说明这个数是快乐数（1的平方还是1，最后left和right指针会停在这里)
如果相遇的位置不为1，则不是快乐数

代码

class Solution {
public://返回每位平方和之和int nsum(int n){int sum = 0;while(n){int x = n%10;sum+=x*x;n/=10;}return sum;}bool isHappy(int n) {int slow = n;int fast = nsum(n);while(slow!=fast){slow = nsum(slow);fast = nsum(nsum(fast));}return slow == 1;}
};
``![在这里插入图片描述](https://img-blog.csdnimg.cn/direct/8ba1fa18f1704bbfa7d26bb3632f79f0.png)