2023.8.10

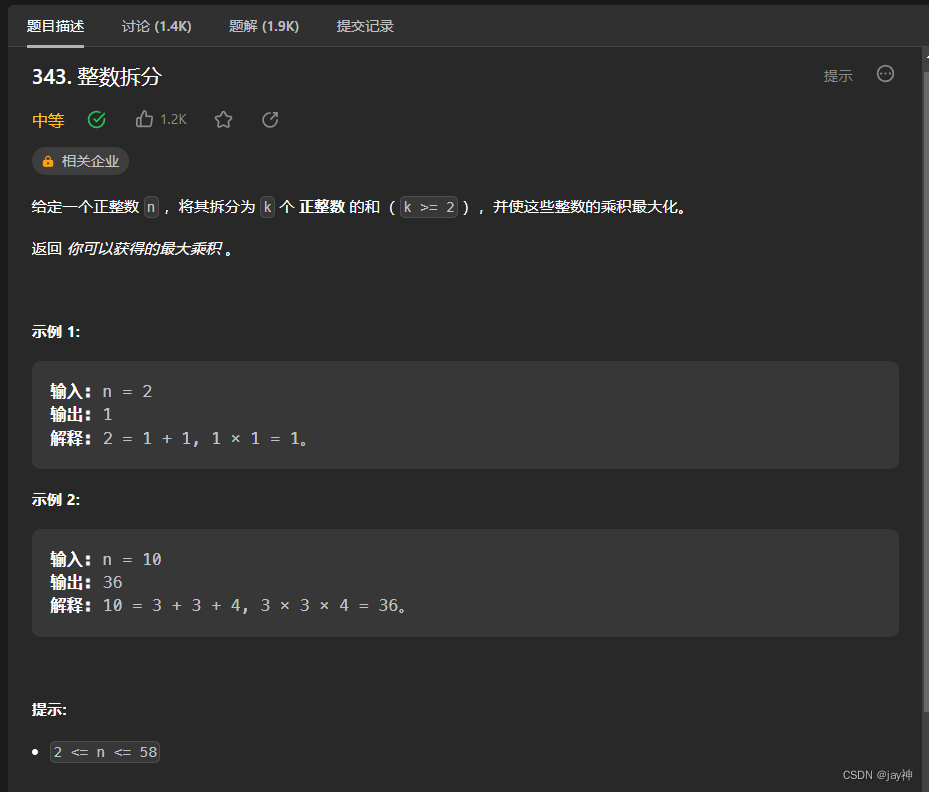
       本题用dp算法来做，dp[i]代表的含义是：当前数字i 在拆分之后所能获得的最大乘积。然后由于n>=2，所以dp[0]和dp[1]没有意义，不用初始化，直接初始化dp[2]= 1。  然后再遍历给dp数组赋值：dp[i]的来源有两个：①将i拆成 j 和 (i - j) ，然后相乘，即j*(i-j)。 ② 将i 拆成 j 和(i-j), 然后(i-j)的最大拆分乘积为dp[i-j]，即 j * dp[i-j]。 

        思考画的草图：

        代码如下： 

class Solution {
public:int integerBreak(int n) {vector<int> dp(n+1); //dp[i]的含义是：当前数字i拆分之后的最大乘积值。dp[2] = 1; //初始化//遍历赋值for(int i=3; i<=n; i++){for(int j=1; j<=i/2; j++){dp[i] = max(dp[i] , max(j*(i-j),j*dp[i-j]));}}return dp[n];}
};