题目 表达式\[\tan^2 \frac {\pi}{16} \cdot \tan^2 \frac {3\pi}{16} + \tan^2 \frac {\pi}{16} \cdot \tan^2 \frac {5\pi}{16}+\tan^2 \frac {3\pi}{16} \cdot \tan^2 \frac {7\pi}{16}+\tan^2 \frac {5\pi}{16} \cdot \tan^2 \frac {7\pi}{16}\]的值为
$\textbf{(A) } 28 \qquad \textbf{(B) } 68 \qquad \textbf{(C) } 70 \qquad \textbf{(D) } 72 \qquad \textbf{(E) } 84$
解 注意到表达式可以因式分解为$\left(\tan^2 \dfrac {\pi}{16}+\tan^2 \dfrac {7\pi}{16}\right)\left(\tan^2 \dfrac {3\pi}{16}+\tan^2 \dfrac {5\pi}{16}\right),$ 而\begin{align*}&\tan^2 x+\tan^2 \left(\dfrac{\pi }{2}-x\right)=\dfrac{\sin^2x}{\cos^2x}+\dfrac{\cos^2x}{\sin^2x}=\dfrac{\sin^4x+\cos^4x}{\sin^2x\cos^2x}\\=&\dfrac{(\sin^2x+\cos^2x)^2-2\sin^2x\cos^2x}{\sin^2x\cos^2x}=\dfrac{4}{\sin^22x}-2=\dfrac{8}{1-\cos4x}-2. \end{align*}因此$\tan^2 \dfrac {\pi}{16}+\tan^2 \dfrac {7\pi}{16}=\dfrac{8}{1-\cos\frac{\pi}{4}}-2=14+8\sqrt2,$ $\tan^2 \dfrac {3\pi}{16}+\tan^2 \dfrac {5\pi}{16}=\dfrac{8}{1-\cos\frac{3\pi}{4}}-2=14-8\sqrt2,$ 因此原表达式的值为$(14+8\sqrt2)\times(14-8\sqrt2)=68.$ 选$\textbf{(B) }.$
2024年美国数学竞赛12年级组A卷P23:合适的一试题
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.hqwc.cn/news/832997.html
如若内容造成侵权/违法违规/事实不符,请联系编程知识网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
(系列十一)Vue3框架中路由守卫及请求拦截(实现前后端交互)
说明该文章是属于OverallAuth2.0系列文章,每周更新一篇该系列文章(从0到1完成系统开发)。该系统文章,我会尽量说的非常详细,做到不管新手、老手都能看懂。说明:OverallAuth2.0 是一个简单、易懂、功能强大的权限+可视化流程管理系统。
友情提醒:本篇文章是属于系列文章,…
MIGO DUMP LCX_RAP_EVENT_RUNTIME CL_RAP_EVENT_MANAGER==========CP
MIGO 收货时发生DUMP运行事务代码:SBGRFCCONF
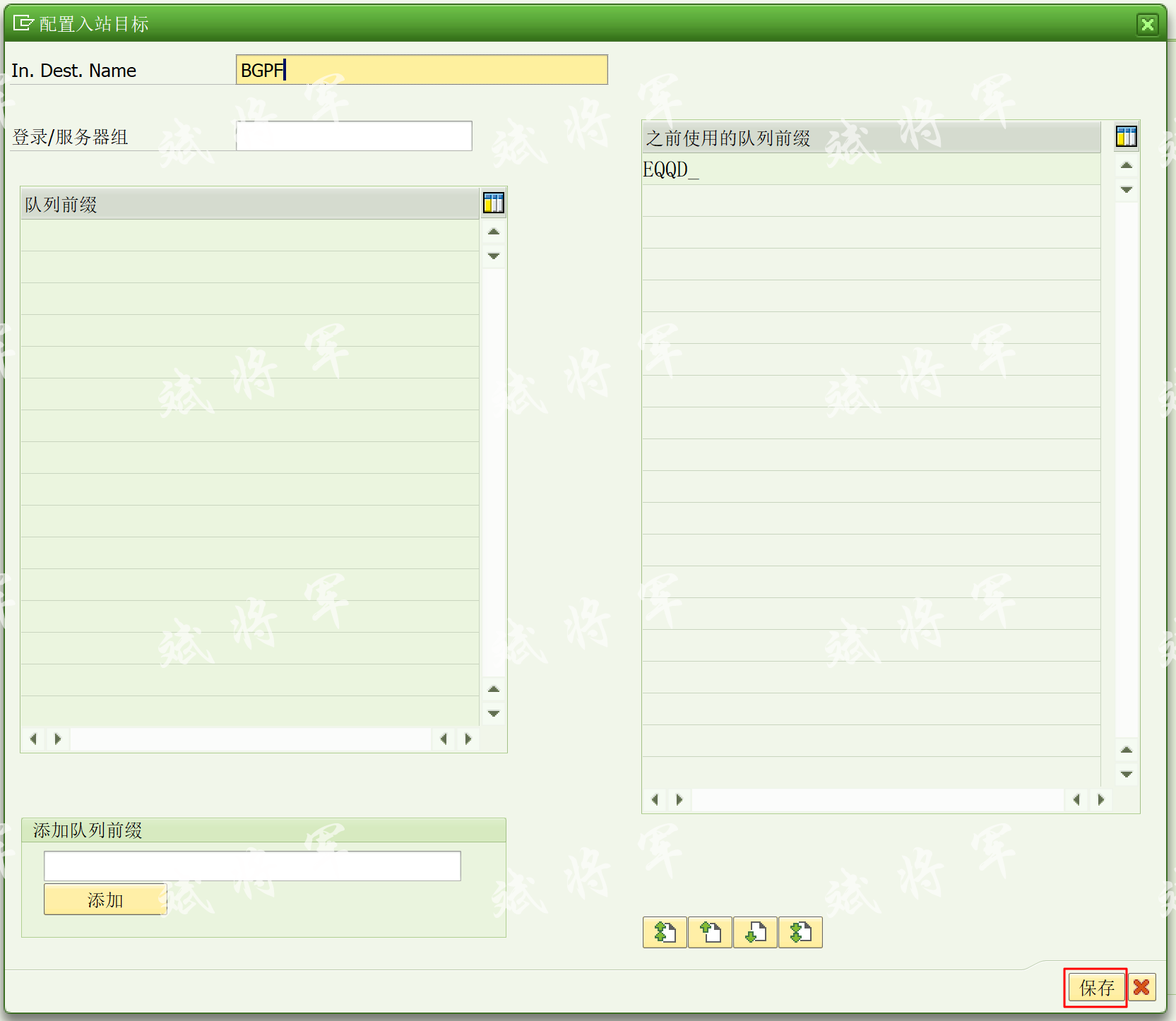
创建入站目标输入目标BGPF 保存即可TRANSLATE with xEnglishArabic
Hebrew
PolishBulgarian
Hindi
PortugueseCatalan
Hmong Daw
RomanianChinese Simplified
Hungarian
RussianChinese Traditional
Indonesian
SlovakCzech
Ital…
非煤矿山算法智慧矿山一体机提升机危险区域违规闯入识别边坡监测预警系统详述
在矿山行业中,安全始终是最为关键的议题。随着智能化技术的发展,智慧矿山一体机应运而生,它专为矿山安全监控和管理设计,集成了多种智能化功能,以提升矿山的安全监管能力和生产效率。这款设备不仅能够满足矿山场景下的视频智能化建设需求,还能够通过边缘计算技术实现对矿…
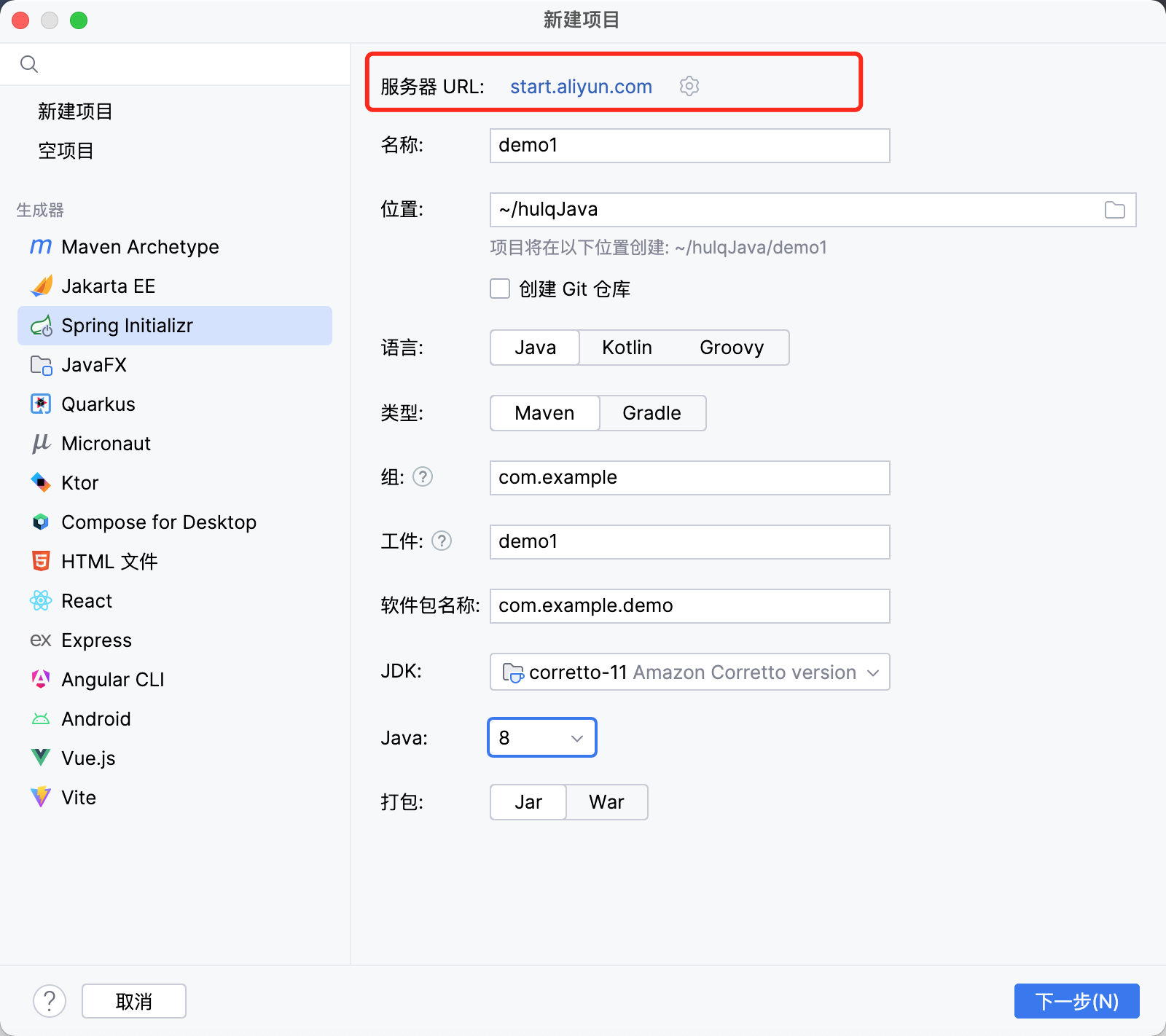
使用idea创建Sping Boot 项目 发现不能使用JAVA版本是8或者11版本只能用17版本已经更高
接下来需要一个骚操作, 官方地址: https://start.spring.io阿里云脚手架地址:https://start.aliyun.com/
[题解]P3225 [HNOI2012] 矿场搭建
P3225 [HNOI2012] 矿场搭建
挖煤点坍塌相当于把该点和与其相连的边在图上删掉。
借用wjyyy的题解,我们定义“叶子连通块”为“只包含\(1\)个割点的点双连通分量”,“非叶子连通块”为“包含\(\ge 2\)个割点的点双连通分量”。
如下图,橙色点是割点,红色框圈出的是点双,加粗…
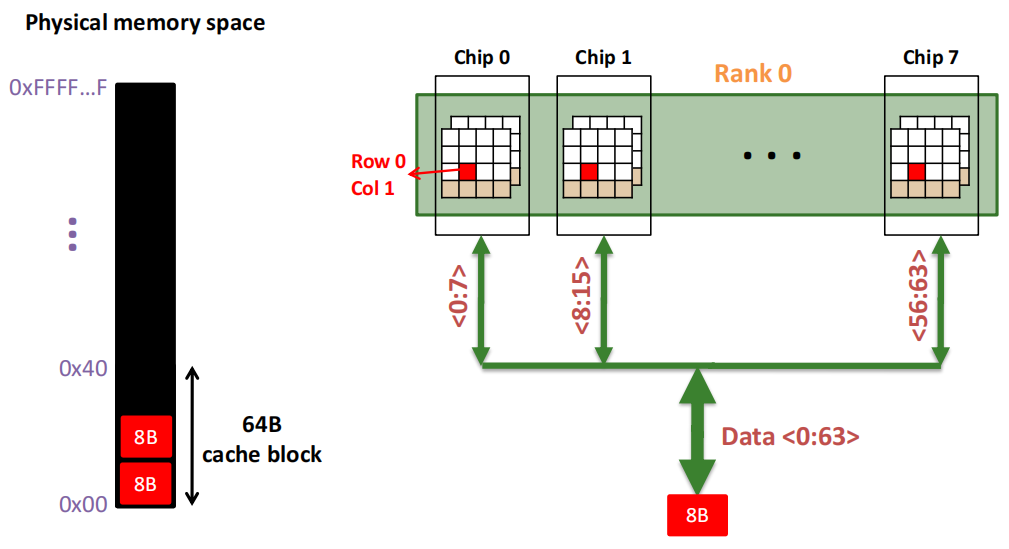
DDCA —— 内存架构和子系统内存控制器
Digital Design and Computer Architecture Lecture21的学习笔记,介绍内存架构和子系统、内存控制器,并详细介绍了DRAM的内部结构。1. 内存架构和子系统
1.1 如何控制访问?访问控制:存储单元的访问是通过 访问晶体管(access transistors) 进行控制的。访问晶体管像开关一…
ubuntu上安装 NVIDIA GeForce RTX 4090驱动
背景
ai服务器上安装完ubuntu系统后,需要安装NVIDIA显卡驱动
官网驱动下载https://www.nvidia.cn/drivers/details/235646/驱动安装
1.卸载原有驱动
sudo apt remove --purge nvidia*2.备份
sudo cp /etc/modprobe.d/blacklist.conf /etc/modprobe.d/blacklist.conf_bak
3.末尾…
springboot将文件处理成压缩文件
前言
在工作我们经常会出现有多个文件,为了节省资源会将多个文件放在一起进行压缩处理;为了让大家进一步了解我先将springboot处理的方法总结如下,有不到之处敬请大家批评指正!
一、文件准备:https://qnsc.oss-cn-beijing.aliyuncs.com/crmebimage/public/product/2024/11…
CMDB平台(进阶篇):CMDB的构建指南(一)
CMDB(配置管理数据库)的构建是一个复杂而细致的过程,其中组建项目团队和定义项目是至关重要的初始阶段。以下是根据高权威性来源整理的,关于这两个阶段的详细指南:
一、组建项目团队
团队角色与技能:
选择的团队必须具备相应的技能、经验、知识去解释、设计和实施一个CMD…



![[题解]P3225 [HNOI2012] 矿场搭建](https://img2024.cnblogs.com/blog/3322276/202411/3322276-20241113130148298-1319845583.png)