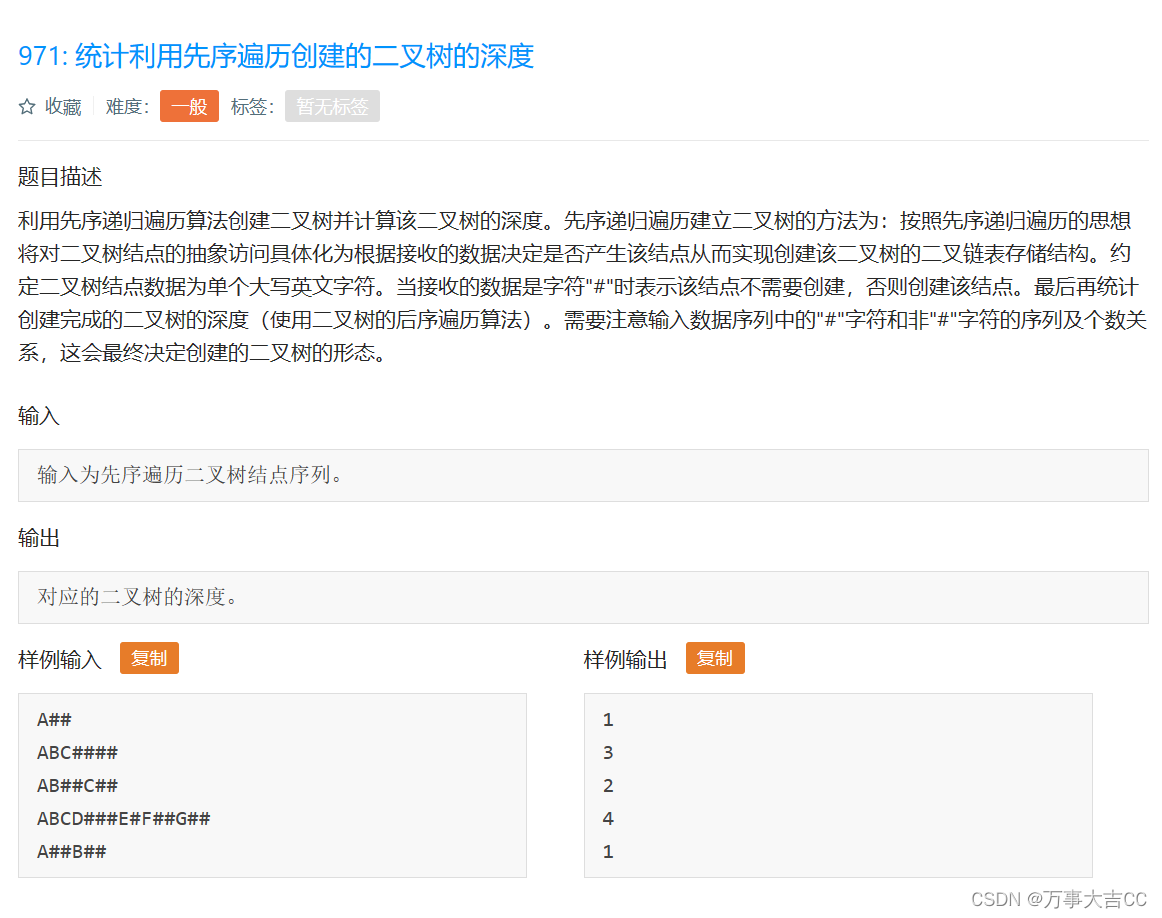
解法:
1.先序遍历创建二叉树链表形式
2.求二叉树的深度
用后序遍历实现:
1.后序遍历求节点A左右子树高度
2.对节点A:
1.取左右子树较大高度
2.返回高度+1(即以节点A为根节点的子树的最大深度)
例如

#include <iostream>
using namespace std;
// 定义二叉树结点
struct TreeNode {char val;TreeNode* left;TreeNode* right;TreeNode(char x) :val(x), left(NULL), right(NULL) {};
};
// 先序递归遍历建立二叉树
TreeNode* buildTree() {char c;cin >> c;if (c == '#') {return NULL;}TreeNode* root = new TreeNode(c);root->left = buildTree();root->right = buildTree();return root;
}
// 后序遍历计算二叉树深度
int getDepth(TreeNode* root) {if (root == NULL) {return 0;}else {int leftDepth = getDepth(root->left);int rightDepth = getDepth(root->right);return max(leftDepth, rightDepth) + 1;}
}
int main() {TreeNode* root= buildTree();cout<<getDepth(root);return 0;
}
由于树的最大深度=树的高度=层数
可以用层序遍历
#include<iostream>
#include<queue>
using namespace std;
// 定义二叉树结点
struct TreeNode {char val;TreeNode* left;TreeNode* right;TreeNode(char x) :val(x), left(NULL), right(NULL) {};
};
// 先序递归遍历建立二叉树
TreeNode* buildTree() {char c;cin >> c;if (c == '#') {return NULL;}TreeNode* root = new TreeNode(c);root->left = buildTree();root->right = buildTree();return root;
}
// 计算二叉树深度
int getDepth(TreeNode* root) {int result = 0;queue<TreeNode*> q;q.push(root);while (!q.empty()) {result++;for (int i = 0; i < q.size(); i++) {TreeNode* cur = q.front();q.pop();if (cur->left) q.push(cur->left);if (cur->right) q.push(cur->right);}}return result;
}
int main() {TreeNode* root= buildTree();cout<<getDepth(root);return 0;
}