深入了解数据结构第四弹——排序（1）——插入排序和希尔排序-编程知识

前言：

从本篇开始，我们就开始进入排序的学习，在结束完二叉树的学习之后，相信我们对数据在内存中的存储结构有了新的认识，今天开始，我们将进入排序的学习，今天来学习第一篇——插入排序

什么是插入排序？

一、直接插入排序

1、直接插入排序的实现

2、直接插入排序的时间复杂度

二、希尔排序

1、希尔排序的实现

2、希尔排序的时间复杂度

三、直接插入排序和希尔排序时间复杂度的比较

四、总结

首先，我们先来了解一下几种排序算法都有什么，方便我们后期学习，今天，我们先来讲解插入排序

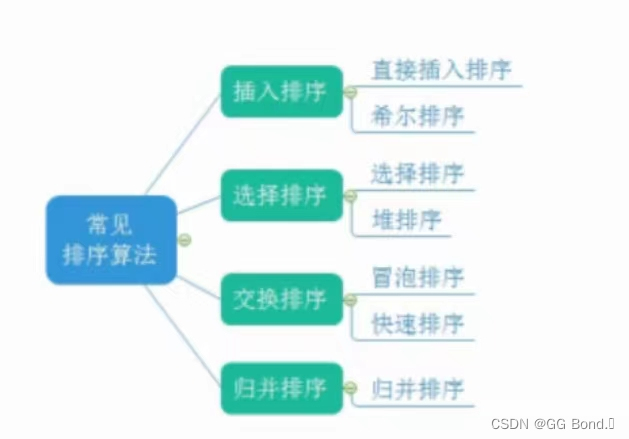
什么是插入排序？

插入排序其实挺有意思，这种排序方法在我们生活中也挺常见，例如，当我们在打扑克的时候，当我们再次摸牌时，我们会将新牌按照大小顺序插入到旧牌中

插入排序实际上就是将一个数字按照大小顺序插入到已知的序列中去

一、直接插入排序

1、直接插入排序的实现

插入排序是从后往前比较的，例如

当我们对这样一个数组进行插入排序时，我们先将1放进去，然后再放进去2与1比较，再放进去4与前面的1和2比较，以此类推，每放进去一个数字与前面数字比较，所以插入排序的过程是需要遍历数组的，我们首先可以给一个end变量标记现在排好序的数组的末端位置，再给出一个tmp变量来表示要排序的数字

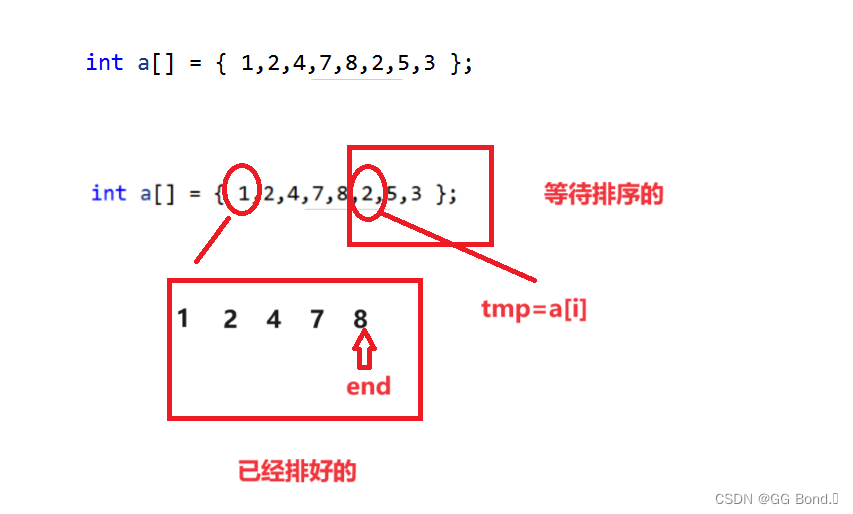
插入排序的代码如下：（降序）

void InsertSort(int* a, int n)
{for (int i = 1; i < n; i++){int end = i - 1;int tmp=a[i];while (end>=0){if (tmp > a[end]){a[end + 1] = a[end];end--;}else{break;}}a[end + 1] = tmp;}
}

通过这段代码我们就可以看出插入排序的规则：当插入数据大于end位置的数据时，让end位置的数据向后移动一位，同时让end位置存放新插入的数据；当插入数据小于end位置数据时，那就直接让插入数据存放在end加1的位置就行

我们建立一个完整的代码示例并打印结果，给大家看看效果


//插入排序
void PrintArray(int* a, int n)
{for (int i = 0; i < n; i++){printf("%d ", a[i]);}printf("\n");
}
void InsertSort(int* a, int n)
{for (int i = 1; i < n; i++){int end = i - 1;int tmp = a[i];while (end >= 0){if (tmp > a[end]){a[end + 1] = a[end];end--;}else{break;}}a[end + 1] = tmp;}
}void TestInsertSort()
{int a[] = { 1,2,4,7,8,2,5,3 };PrintArray(a, sizeof(a) / sizeof(a[0]));InsertSort(a, sizeof(a) / sizeof(a[0]));PrintArray(a, sizeof(a) / sizeof(a[0]));
}
int main()
{TestInsertSort();return 0;
}

运行结果：

第一行是排序前，第二行是排序后

2、直接插入排序的时间复杂度

时间复杂度最坏O(N^2)
时间复杂度最好O(N)

如图所示：

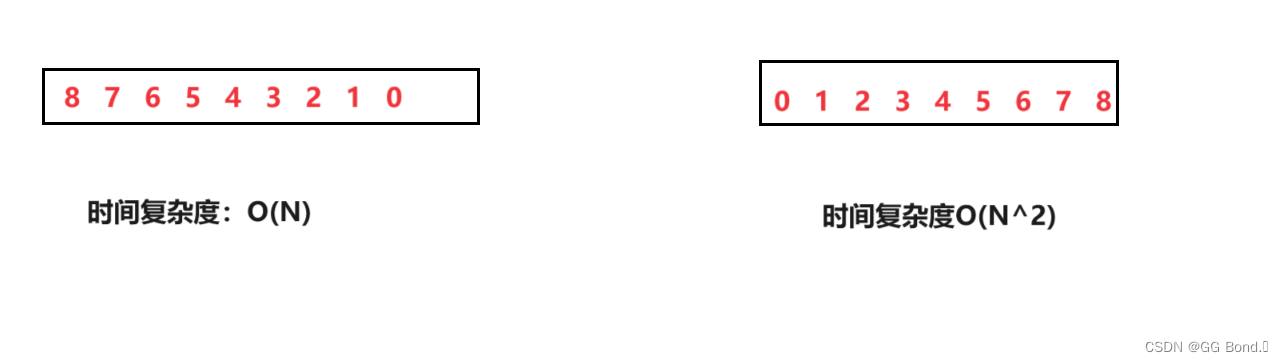
不同的两组数据在用直接插入排序降序时，左边时间复杂度明显小于右边

综上，其实综合来说直接插入排序的时间复杂度是介于O(N)和O(N^2)之间的

二、希尔排序

1、希尔排序的实现

希尔排序是插入排序的改进，它通过将待排序的数据分割成若干个子序列来提高插入排序的效率。希尔排序的基本思想是：先将整个待排序的序列分割成若干个子序列，然后对这些子序列分别进行插入排序，最后再对整个序列进行一次插入排序。

希尔排序的具体步骤如下：

选择一个增量序列，通常是按照一定规则递减的序列，最常用的是取增量序列为n/2，n/4，n/8...1，后来经过改进，一般选择n/3+1来确保程序的稳定性
根据增量序列的值，将待排序序列分割成若干个子序列，对每个子序列进行插入排序。
逐渐缩小增量，重复第2步，直到增量为1。
最后对整个序列进行一次插入排序

例如：对于{9，8，7，6，5，4，3，2，1，0}这样一组数据，用希尔排序排升序的步骤如下：

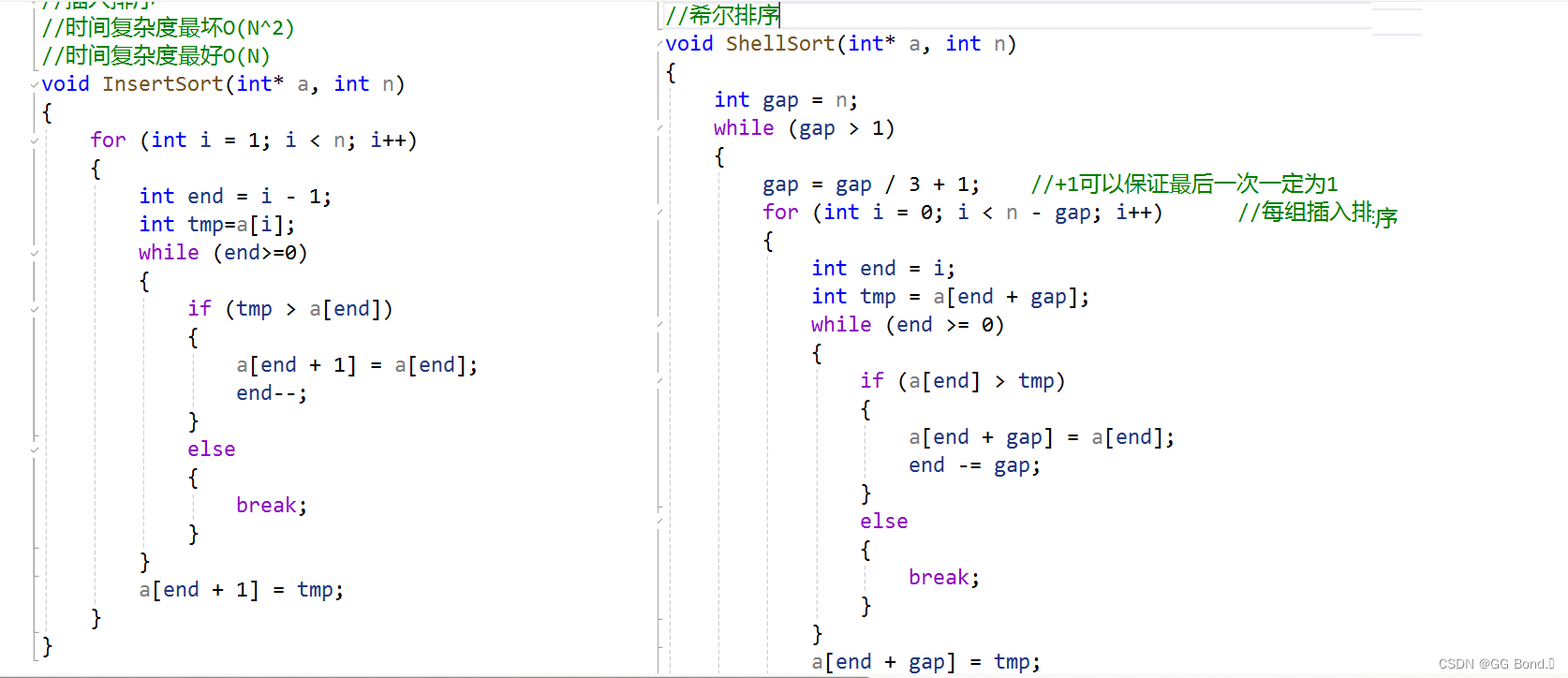
实现上图功能的代码如下：

void ShellSort(int* a, int n)
{int gap = n;while (gap > 1){gap = gap / 3 + 1;    //+1可以保证最后一次一定为1for (int i = 0; i < n - gap; i++)      //每组插入排序{int end = i;int tmp = a[end + gap];while (end >= 0){if (a[end] > tmp){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}
}

这个过程跟插入排序相似度很高，可以将两者放在一起比较体会一下

希尔排序的完整代码示例：

void PrintArray(int* a, int n)
{for (int i = 0; i < n; i++){printf("%d ", a[i]);}printf("\n");
}
void ShellSort(int* a, int n)
{int gap = n;while (gap > 1){gap = gap / 3 + 1;    //+1可以保证最后一次一定为1for (int i = 0; i < n - gap; i++)      //每组插入排序{int end = i;int tmp = a[end + gap];while (end >= 0){if (a[end] > tmp){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}
}
void TestShell()
{int a[] = { 9,8,7,6,5,4,3,2,1,0 };printf("排序前：");PrintArray(a, sizeof(a) / sizeof(0));ShellSort(a, sizeof(a) / sizeof(0));printf("排序后：");PrintArray(a, sizeof(a) / sizeof(0));
}
int main()
{TestShell();return 0;
}

运行结果：

2、希尔排序的时间复杂度

希尔排序的时间复杂度取决于增量序列的选择，一般情况下，希尔排序的时间复杂度为O(n log n)到O(n^2)之间。希尔排序是不稳定的排序算法，因为在排序过程中会改变相同元素之间的相对位置，所以希尔排序的时间复杂度其实并不能真正的计算出来，但希尔排序仍然要比直接排序要高效的多，我们可以通过一些方式来检验这种高效性

三、直接插入排序和希尔排序时间复杂度的比较

我们可以通过clock()函数来检验他们两个的时间复杂度

void TestOP()
{srand(time(0));const int N = 10000;int* a1 = (int*)malloc(sizeof(int) * N);int* a2 = (int*)malloc(sizeof(int) * N);int* a3 = (int*)malloc(sizeof(int) * N);for (int i = 0; i < N; i++)       //让这两个算法都处理一万组数据，比较他们两个用时长短{a1[i] = rand();a2[i] = a1[i];a3[i] = a1[i];}int begin1 = clock();  InsertSort(a1, N);int end1 = clock();int begin2 = clock();ShellSort(a2, N);int end2 = clock();printf("InsertSort:%d\n", end1 - begin1);  //直接插入排序所用时间printf("ShellSort:%d\n", end2 - begin2);   //希尔排序所用时间
}

运行结果：