1.16 LeetCode总结（基本算法）动态规划2-编程知识

70. 爬楼梯

在这里插入图片描述
首先想到的是递归：

// 递归
int climbStairs(int n) {if (n == 1) {return 1;} else if (n == 2) {return 2;}return climbStairs(n - 1) + climbStairs(n - 2);
}

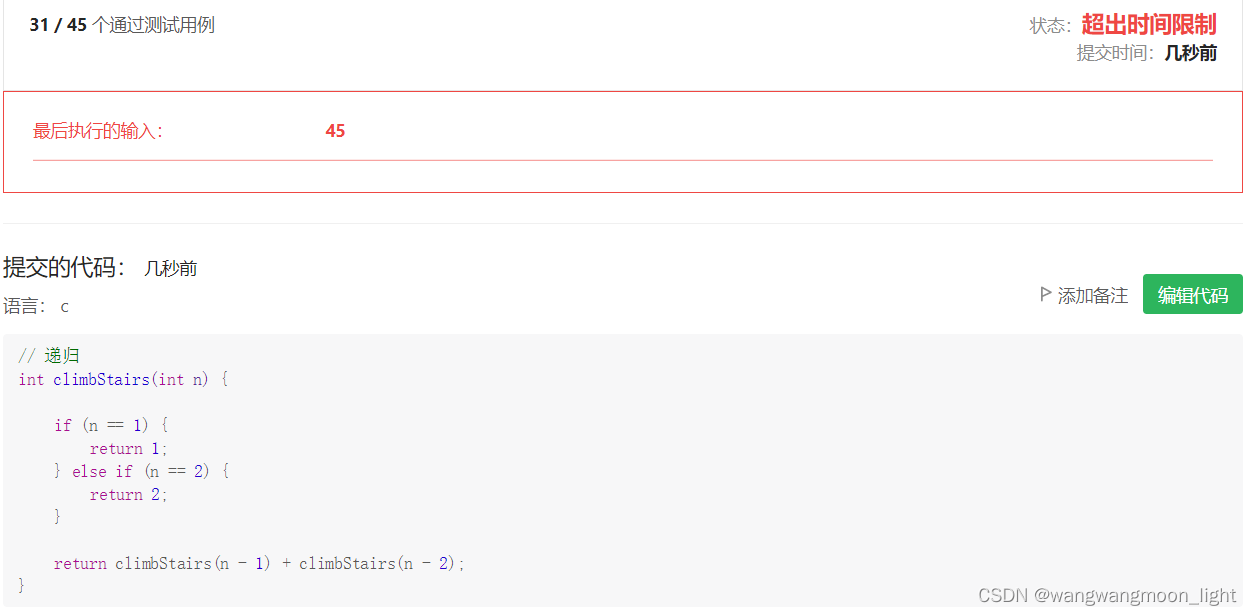
在这里插入图片描述
我们先来看看这个递归的时间复杂度吧：

递归时间复杂度 = 解决一个子问题时间*子问题个数
一个子问题时间 = f(n-1)+ f(n-2)，也就是一个加法的操作，所以复杂度是 O(1)；
问题个数 = 递归树节点的总数，递归树的总节点 = 2^{n-1，所以是复杂度O(2}n)。
因此，青蛙跳阶，递归解法的时间复杂度 = O(1) * O(2^n) = O(2^n)，就是指数级别的，爆炸增长的，如果n比较大的话，超时很正常的了。

回过头来，你仔细观察这颗递归树，你会发现存在大量重复计算，比如 f(8) 被计算了两次，f(7) 被重复计算了3次…所以这个递归算法低效的原因，就是存在大量的重复计算！

既然存在大量重复计算，那么我们可以先把计算好的答案存下来，即造一个备忘录，等到下次需要的话，先去备忘录查一下，如果有，就直接取就好了，备忘录没有才开始计算，那就可以省去重新重复计算的耗时啦！这就是带备忘录的解法。

自底向上的动态规划
动态规划跟带备忘录的递归解法基本思想是一致的，都是减少重复计算，时间复杂度也都是差不多。但是呢：

带备忘录的递归，是从f(10)往f(1）方向延伸求解的，所以也称为自顶向下的解法。
动态规划从较小问题的解，由交叠性质，逐步决策出较大问题的解，它是从f(1)往f(10）方向，往上推求解，所以称为自底向上的解法。
动态规划有几个典型特征，最优子结构、状态转移方程、边界、重叠子问题。在青蛙跳阶问题中：

f(n-1) 和 f(n-2) 称为 f(n) 的最优子结构
f(n) = f(n-1) + f(n-2) 就称为状态转移方程
f(1) = 1, f(2) = 2 就是边界啦
比如f(10)= f(9)+f(8), f(9) = f(8) + f(7) , f(8)就是重叠子问题。
我们来看下自底向上的解法，从 f(1) 往 f(10) 方向，想想是不是直接一个for循环就可以解决啦，如下：
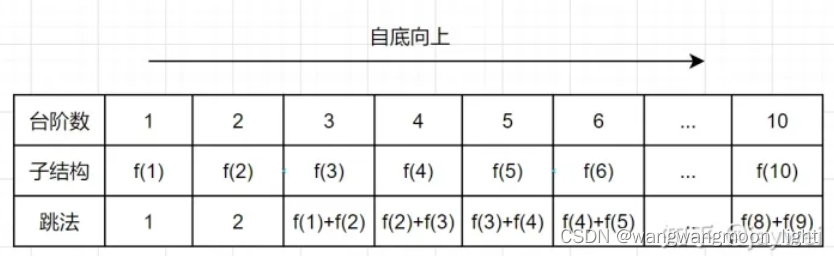
在这里插入图片描述

int climbStairs(int n){//f(x) = f(x-1) + f(x-2) if (n <= 1){ // 第0阶和第1阶只有一种方法return 1;}int way;int memo[2] = {1,1};for (int i = 2; i <= n; ++i) {// 上楼梯->从第2阶楼梯开始way = memo[0] + memo[1];memo[0] = memo[1];memo[1] = way;}return way;
}

动态规划的解题思路
动态规划的核心思想就是拆分子问题，记住过往，减少重复计算。并且动态规划一般都是自底向上的，因此到这里，基于青蛙跳阶问题，我总结了一下我做动态规划的思路：

穷举分析
当台阶数是1的时候，有一种跳法，f(1) = 1
当只有2级台阶时，有两种跳法，第一种是直接跳两级，第二种是先跳一级，然后再跳一级。即f(2) = 2;
当台阶是3级时，想跳到第3级台阶，要么是先跳到第2级，然后再跳1级台阶上去，要么是先跳到第 1级，然后一次迈 2 级台阶上去。所以f(3) = f(2) + f(1) = 3
当台阶是4级时，想跳到第3级台阶，要么是先跳到第3级，然后再跳1级台阶上去，要么是先跳到第 2级，然后一次迈 2 级台阶上去。所以f(4) = f(3) + f(2) = 5
当台阶是5级时…

确定边界
通过穷举分析，我们发现，当台阶数是1的时候或者2的时候，可以明确知道青蛙跳法。f（1） =1，f(2) = 2，当台阶n>=3时，已经呈现出规律f(3) = f(2) + f(1) =3，因此f（1） =1，f(2) = 2就是青蛙跳阶的边界。

找出规律，确定最优子结构
n>=3时，已经呈现出规律 f(n) = f(n-1) + f(n-2) ，因此，f(n-1)和f(n-2) 称为 f(n) 的最优子结构。什么是最优子结构？有这么一个解释：一道动态规划问题，其实就是一个递推问题。假设当前决策结果是f(n),则最优子结构就是要让 f(n-k) 最优,最优子结构性质就是能让转移到n的状态是最优的,并且与后面的决策没有关系,即让后面的决策安心地使用前面的局部最优解的一种性质

写出状态转移方程
通过前面3步，穷举分析，确定边界，最优子结构，我们就可以得出状态转移方程啦

代码实现
我们实现代码的时候，一般注意从底往上遍历，然后关注下边界情况，空间复杂度，也就差不多啦。动态规划有个框架的，大家实现的时候，可以考虑适当参考一下:

dp[0][0][...] = 边界值
for (状态1 ：所有状态1的值) {for (状态2 ：所有状态2的值) {for (...) {// 状态转移方程dp[状态1][状态2][...] = 求最值}}
}

118. 杨辉三角

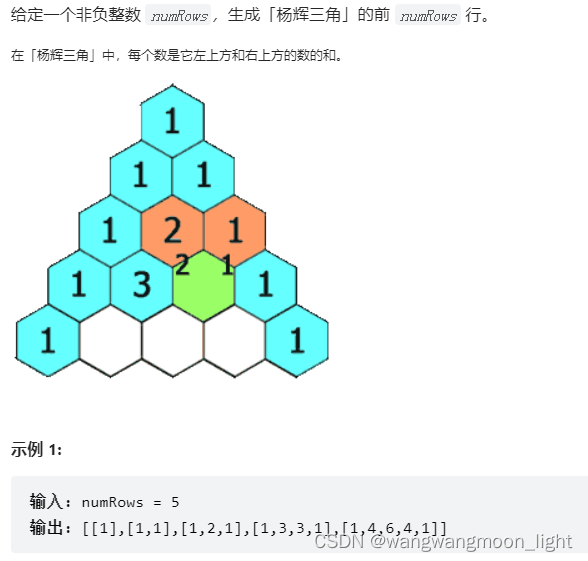
在这里插入图片描述

int **generate(int numRows, int *returnSize, int **returnColumnSizes)
{int **res = (int **)malloc(sizeof(int *) * numRows);;*returnSize = numRows; // 行个数*returnColumnSizes = (int *)malloc(sizeof(int) * numRows); // 一维数组，每个元素代表了当前排有多少个有效的列printf("int *%d\n", sizeof(int *));printf("int %d\n",  sizeof(int));for (int i = 0; i < numRows; ++i) {res[i] = (int *)malloc(sizeof(int) * (i + 1));(*returnColumnSizes)[i] = i + 1; // 列元素个数res[i][0] = res[i][i] = 1;for (int j = 1; j < i; ++j) {res[i][j] = res[i - 1][j - 1] + res[i - 1][j];}}return res;
}

在LeetCode里 Sizeof(int *) 和 Sizeof(int)的大小时不一样的，注意：

C 动态规划举例

在这里插入图片描述
手法1. 首先容易想到的是使用递归来求解，但递归的效率很低

// 递归 
int climbStairs(int n) {if (n <= 2) {return n;}return climbStairs(n - 1) + climbStairs(n - 2);
}

其实记忆化搜索就是在递归的条件上，为减少递归次数而产生的
比如下述代码中对于 mem[n] !=0 直接return memo[n].
我们总是习惯自顶向下思考问题，而不容易自底向上思考问题

手法2：记忆化搜索 – 自顶向下

// 记忆化搜索 -- 自顶往下
int memo[64] = { 0 };
int climbStairs(int n) {if (n <= 2) {return n;}// 如果满足条件则直接返回记忆数组里的值，减少递归次数if (n < 64 && memo[n] != 0) {return memo[n];}// 不满足条件才进行递归 O(n)memo[n] = climbStairs(n-1) + climbStairs(n-2);return memo[n];
}

手法3：动态规划 – 自底往上

// 动态规划 -- 自底往上
int climbStairs(int n) {if (n <= 2) {return n;}int a1 = 1;int a2 = 2;int memo = 0;// 自下而上的进行计算，动态规划for (int i = 3; i <= n; i++) {memo = a1 + a2;a1  = a2;a2  = memo;}return memo;
}

动态规划，将原问题拆解成若干子问题，同时保存子问题的答案，使得每个子问题只求解一次，最终获得原问题的答案；
下面这个图非常清晰地说明了动态规划的引入

D 0-1背包问题

– 动态规划中可以解决的一类最为经典的问题 – 01背包问题
在这里插入图片描述
状态转移方程：

调试程序可以采用如下图片的数据，利于理解背包算法：
建立一个 3*6 二维数组，第0行只考虑第0个物品；第一行考虑 a[1][2]的weight为2，既可以放在id0的物品，也可以放下id1的物品；但两者相比，id1的物品要大一些，我们考虑放id1的物品。

在这里插入图片描述
如图，在放置a[1][2]这个元素时考虑：如果不放 ID1 的物品，那么背包价值为6，如果考虑放 ID1 的物品，需要回到a[0][0]的价值，加上放 ID1 物品的价值和为10，两者比较（10 > 6），放的价值大，所以考虑放 ID1的物品。
继续布满这个图，则得到下图:
在这里插入图片描述
如图，在放置a[2][4]这个元素时考虑：如果不放 ID2 的物品，那么背包价值为16，如果考虑放 ID2 的物品，需要回到a[1][1]的价值 6 ，加上放 ID2 物品的价值和为18，两者比较（18 > 16），放的价值大，所以考虑放 ID2的物品。