本专栏内容为：算法学习专栏，分为优选算法专栏，贪心算法专栏，动态规划专栏以及递归，搜索与回溯算法专栏四部分。 通过本专栏的深入学习，你可以了解并掌握算法。

💓博主csdn个人主页：小小unicorn
⏩专栏分类：算法从入门到精通
🚚代码仓库：小小unicorn的代码仓库🚚
🌹🌹🌹关注我带你学习编程知识

寻找数组中心下标

给你一个整数数组 nums ，请计算数组的 中心下标 。

数组 中心下标 是数组的一个下标，其左侧所有元素相加的和等于右侧所有元素相加的和。

如果中心下标位于数组最左端，那么左侧数之和视为 0 ，因为在下标的左侧不存在元素。这一点对于中心下标位于数组最右端同样适用。

如果数组有多个中心下标，应该返回 最靠近左边 的那一个。如果数组不存在中心下标，返回 -1 。

算法原理：

分析题目，既然要找到数组中心下标，我们先假设数组中心为$i$,那么$i$就将数组分成两部分，只要i前面部分的和等于i后面的和，那么此时i就是数组中心，反之就没有数组中心。

前面部分的和我们是可以通过前缀和计算出来的，那么后面的和怎么算呢？其实既然前缀和计算的是前面部分的和，那么后面部分的和我们可以用后缀和来进行计算。

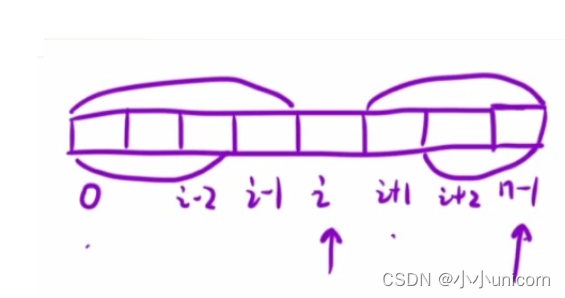
接下来我们要预处理前缀和和后缀和数组：

f[i]表示：[0,i-1]区间所有元素的和。
g[i]表示：[i+1,n-1]区间所有元素的和。

接下来递推：

要想算[0,i-1]区间的和，那么我们可以先算[0,i-2]区间的和再加上[i-1]本身的值。
那么也就是：
$f[i]=f[i-1]+nums[i-1]$;
同理：
$g[i]=g[i+1]+nums[i+1]$;

下来使用前缀和数组：

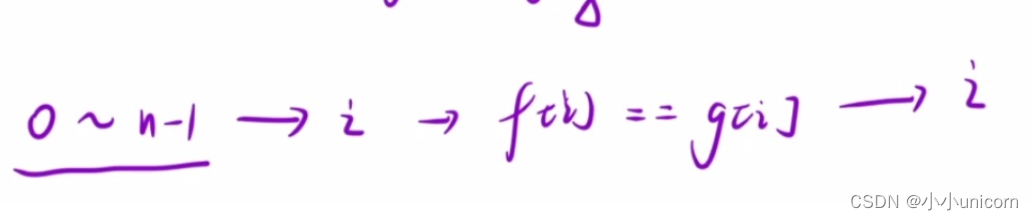
要想求数组中心，那么我们只用判断$f[i]==g[i]$即可，要是相等数组中心就是i位置，反之就是不存在。

介绍到这，原理基本上其实已经就完了，但是在写代码之前还要注意一下细节问题：

为方式越界访问

当下标为0时，$f[0]=f[-1]+nums[0]$;为防止这种情况，我们要让f[0]=0,不影响原始值。

同理，当下标为n-1时，$g[n-1]=g[n]+nums[n-1]$;为防止这种情况，我们要将g[n-1]=0;
当然因为f[i]表示前缀和，因此填表顺序从左往右，相反g[i]填表顺序型右往左。

代码实现：

class Solution 
{
public:int pivotIndex(vector<int>& nums) {int n=nums.size();vector<int> f(n),g(n);//1.预处理前缀和数组//前缀和数组for(int i=1;i<n;i++)f[i]=f[i-1]+nums[i-1];//后缀和数组for(int i=n-2;i>=0;i--)g[i]=g[i+1]+nums[i+1];//使用前缀和数组for(int i=0;i<n;i++){if(f[i]==g[i])return i;}return -1;}
};

除自身以外数组的乘积

给你一个整数数组 nums，返回 数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。

题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。

请 不要使用除法，且在 O(n) 时间复杂度内完成此题。

算法原理：

解法一：暴力+枚举

我们模拟一下题目的行为，每算一个下标，通过暴力枚举的方式将乘积乘起来。但是这样时间复杂度是$O(N^2)$显然会超时。

解法二：前缀和

根据第一题的经验，其实这道题跟第一题基本一模一样。
还是将数组分成两部分：

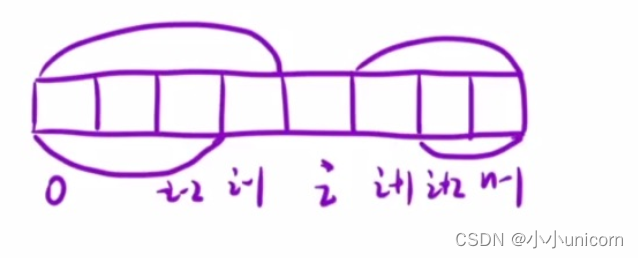
要想计算i位置除i位置其余的乘积，i将数组分成两部分，我们将i位置之前和之后的乘积分别算出来，然后在乘起来就是最终结果。

因此还是用两个数组分别是前缀积和后缀积：

f[i]表示：从[0,i-1]区间内所有元素的乘积。
g[i]表示：从[i+1,n-1]区间内所有元素的乘积。

接下来推递推式子：
有了第一题的经验，本题式子很好推。
$f[i]=f[i-1]\ast nums[i-1]$;
$g[i]=g[i+1]+nums[i+1]$;

使用前缀和数组：
要想拿到i位置的结果，那么我们直接让我们的前缀积和后缀积相乘即可，也就是：
i->f[i]*g[i];

为防止越界，f[0]和g[n-1]要进行初始化，但是此时不能初始化为0，要初始化为1，因为要不影响结果值。

填表顺序：
f[i]：从左往右
g[i]:从右往左；

代码实现：

class Solution 
{
public:vector<int> productExceptSelf(vector<int>& nums) {int n=nums.size();vector<int> f(n),g(n);vector<int> ret(n);f[0]=1;g[n-1]=1;//1.预处理前缀和数组for(int i=1;i<n;i++)f[i]=f[i-1]*nums[i-1];for(int i=n-2;i>=0;i--)g[i]=g[i+1]*nums[i+1];//2.使用前缀和数组for(int i=0;i<n;i++){ret[i]=f[i]*g[i];}return ret;}
};