实现 pow(x, n) ,即计算 x 的整数 n 次幂函数(即,xn )。
暴力方法肯定是循环循环n次,
每一次*x
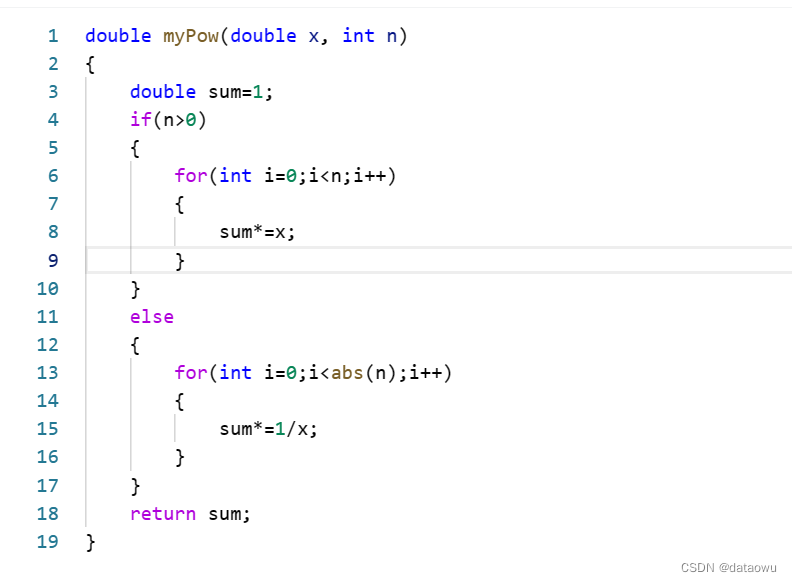
显然此方法遇到大的数字会超时

那么我们要引进一个思想,快速幂算法
例如: x^97
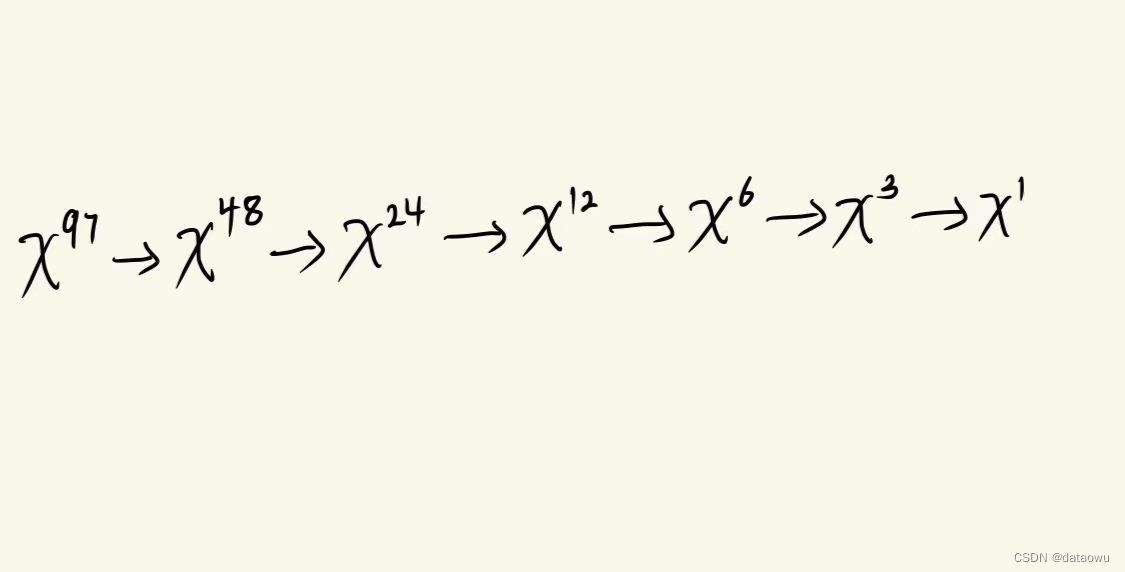
我们可以看出,从右向左
每当n为奇数时,就会多乘一次x
例如:x97 = x48 * x48 * x;
当n为偶数时,不需要此操作
x48 = x24 * x24 ;
由于从0~97 遍历的话 我们不知道何时+1;
所以我们选择从97~0递归

接下来代码实现
double quickly_pow(double x,long long N)
{if(N==0){return 1.00;}else{double y=quickly_pow(x,N/2);return N%2==0?y*y:y*y*x;}
}double myPow(double x, int n)
{long long N=n;return N>0?quickly_pow(x,N):1.0/quickly_pow(x,-N);
}