2023.8.10

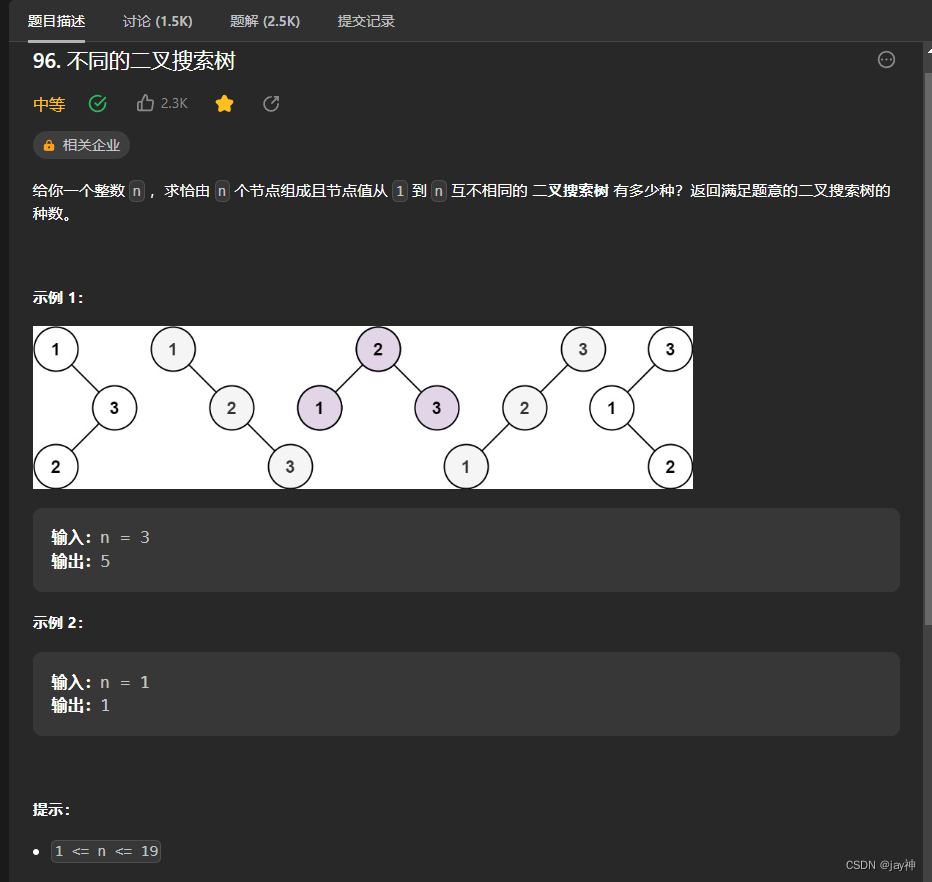
        本题可以先在草稿上画出各种不同的二叉搜索树，从中寻找规律，找出递推关系：

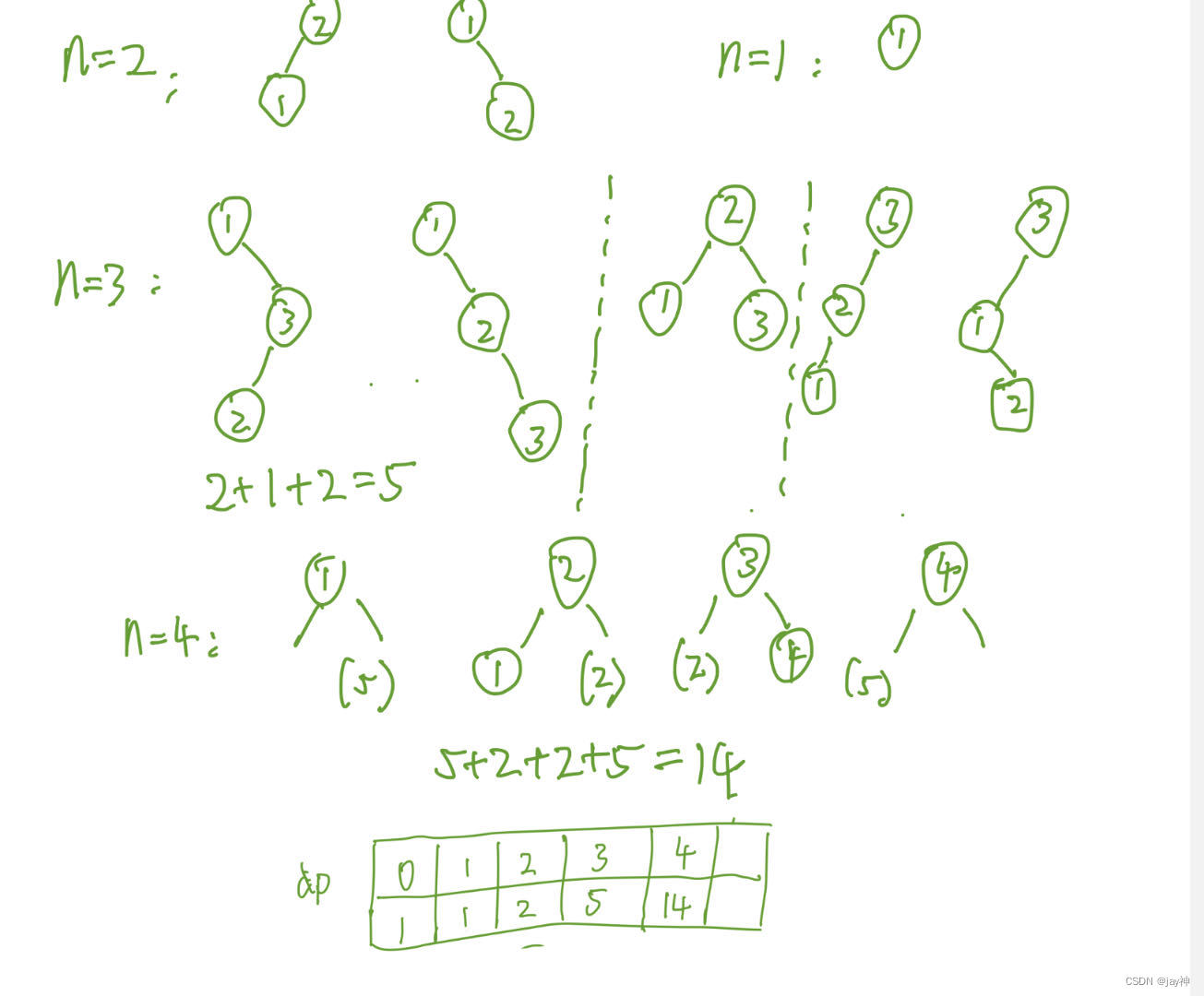
         例如：当n=3时，分三种情况：

①1作为根节点，此时左子树有0个节点，右子树有2两个节点，此时的二叉树种数应该有dp[0]*dp[2]种。

②2作为根节点，此时左右子树各有一个节点，种数都是dp[1]，此时的二叉树种数应该有dp[1]*dp[1]种。

③3作为根节点，此时情况和第一种情况类似，只是左右子树交换了。

        于是可以分析得出：dp[i] 需要从1到 i 进行 i 次累加，每次累加的内容为：dp[左子树的节点个数] * dp[右子树的节点个数]。  代码的步骤如下：

• 定义dp数组，大小为n。 须明确dp[i] 的含义：代表由i个节点组成的二叉搜索树的种数。
• 初始化dp数组，当i=0 或者i=1时，此时二叉搜索树的种数都为1。
• 用两层for循环对dp[i]进行更新。                                           

        具体代码如下：

class Solution {
public:int numTrees(int n) {vector<int> dp(n+1); //dp[i]代表：由i个节点组成的二叉搜索树的种数。dp[0] = 1;dp[1] = 1;for(int i=2; i<=n; i++){for(int j=1; j<=i; j++){dp[i] += dp[j-1] * dp[i-j]; //左子树有j-1个节点，右子树有i-j个节点。}}return dp[n];}
};

        很不错的题目，日后二刷。