dijkstra—所有边均为正权边

1.稠密图

算法思想

将所有的点读入邻接表
外层n次循环
每次找到最近的点，记录这个点的访问状态，使用这个点对其他的点进行更新，最后返回最短路
为什么要记录每个点的状态？我不能重复搜这个点吗？？？
我们的目的是找到最短路径，不能知道原地转，需要向前走，我们不能走回头路

算法步骤：

#include<iostream>
#include<cstring>
using namespace std;
const int N=510;
int g[N][N],d[N],st[N];
//st记录是否被访问过
int n,m;int dijkstra()
{d[1]=0;for(int i=1;i<=n;i++){int t=-1;for(int j=1;j<=n;j++)if(!st[j]&&(t==-1||d[t]>d[j]))t=j;st[t]=true;for(int j=1;j<=n;j++)if(d[j]>d[t]+g[t][j])d[j]=d[t]+g[t][j];}return d[n];
}
int main()
{cin>>n>>m;memset(d,0x3f,sizeof(d));memset(g,0x3f,sizeof(g));while(m--){int a,b,c;cin>>a>>b>>c;g[a][b]=min(g[a][b],c);}int t=dijkstra();if(t==0x3f3f3f3f) puts("-1");else printf("%d\n",t);return 0;
}

2.稀疏图

算法思想

将所有的点读入，因为是邻接表，还是正权边—>dijkstra算法
dijkstra算法需要找到每次的最短的边，所以需要使用优先队列来快速取出最短的距离

算法步骤以及实现

#include<iostream>
#include<cstring>
#include<queue>
#include<vector>
using namespace std;
const int N=3e5+10;
int h[N],e[N],ne[N],idx,w[N],d[N],st[N];
//st表示是否被搜过
int n,m;
typedef pair<int,int> PII;void add(int a,int b,int c)
{e[idx]=b,ne[idx]=h[a],w[idx]=c,h[a]=idx++;
}
int dijkstra()
{//每次拿出最近的点，所以排序的时候需要将距离进行排序//监测他是否被搜过//如果被搜过直接跳过，没有就进行更新//后面被更新的点，没有被搜过那么将他放进堆中priority_queue<PII,vector<PII>,greater<PII>> p;d[1]=0;p.push({0,1});while(p.size()){auto t=p.top();p.pop();int pos=t.second,dis=t.first;if(st[pos]) continue;//如果被搜过就不在搜了st[pos]=true;//如果被搜索过了，更新成truefor(int i=h[pos];~i;i=ne[i]){int j=e[i];if(d[j]>dis+w[i]) d[j]=dis+w[i],p.push({d[j],j});}}return d[n];
}
int main()
{cin>>n>>m;//读入数据并初始化memset(d,0x3f,sizeof(d));memset(h,-1,sizeof(h));while(m--){int a,b,c;cin>>a>>b>>c;add(a,b,c);//有向图}int t=dijkstra();if(t==0x3f3f3f3f) t=-1;printf("%d\n",t);return 0;
}

bellman_fold—存在负权边

算法思想

我们对边进行存储，对所有的边进行访问，使用上次的距离进行更新

算法步骤以及实现

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=10010;
struct Edge
{int a,b,c;
}edge[N];
int n,m,k;
int d[N],last[N];//last记录上次的距离int bellman_fold()
{//在不超过k次的情况下，进行搜索for(int i=0;i<k;i++){//每次记录上次的距离memcpy(last,d,sizeof(d));for(int j=0;j<m;j++){auto e=edge[j];d[e.b]=min(d[e.b],last[e.a]+e.c);}}return d[n];
}
int main()
{cin>>n>>m>>k;//使用结构体进行存储for(int i=0;i<m;i++) cin>>edge[i].a>>edge[i].b>>edge[i].c;//对距离进行初始化memset(d,0x3f,sizeof(d));d[1]=0;int t=bellman_fold();if(t>0x3f3f3f3f/2) puts("impossible");else printf("%d",t);return 0;
}

spfa算法—存在负权边

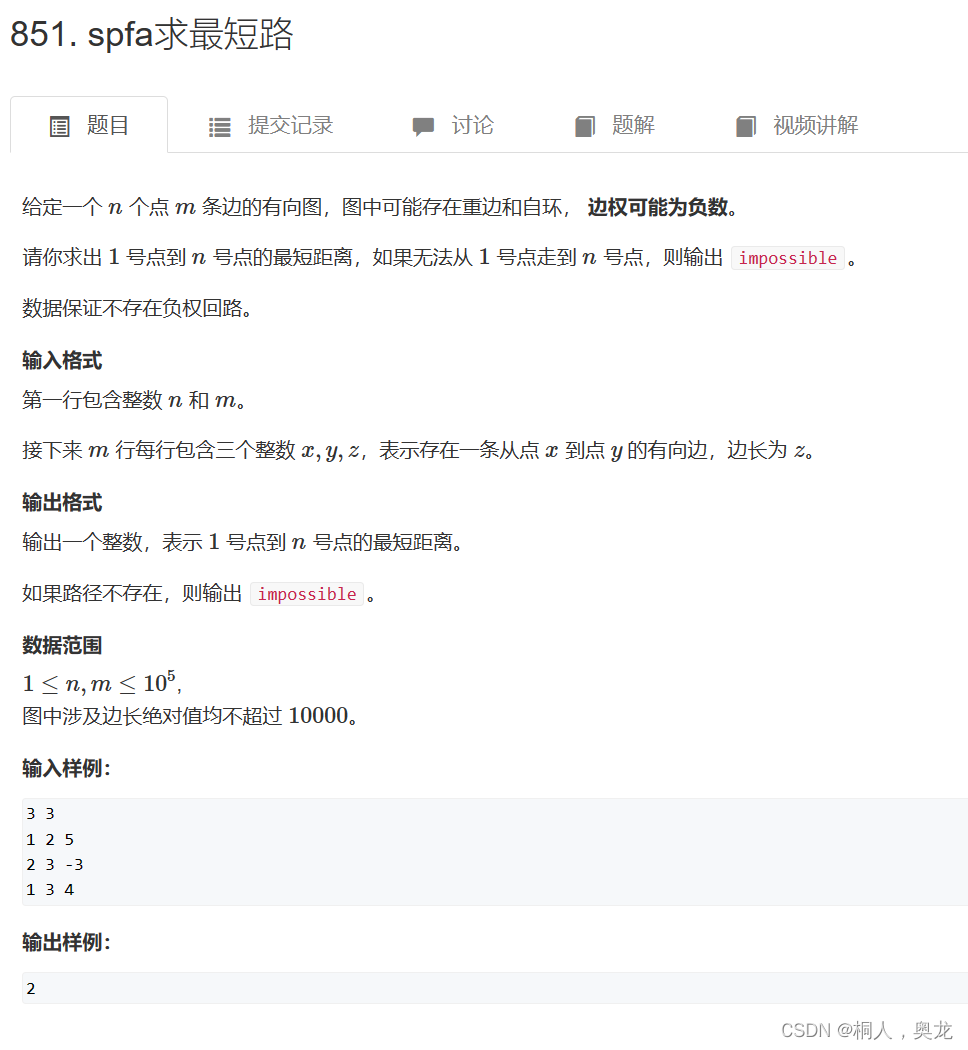
算法思想

spfa是对bellman_fold算法的升级，将出发点加入队列中（队列中的点都是变化的点）
持续从队列中取出一个点，记录这个点没在队列中，判断他的临边是否需要改变如果改变->加入队列并记录在队列中的状态

算法步骤以及实现

#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
const int N=1e5+10;
int h[N],e[N],ne[N],idx,d[N],st[N],w[N];
//st表示是否在队列中
int n,m;void add(int a,int b,int c)
{e[idx]=b,ne[idx]=h[a],w[idx]=c,h[a]=idx++;
}
int spfa()
{d[1]=0;queue<int> q;q.push(1);st[1]=true;while(q.size()){int t=q.front();q.pop();st[t]=false;//表示没有在队列中for(int i=h[t];~i;i=ne[i]){int j=e[i];if(d[j]>d[t]+w[i])//表示需要更新的点，将更新的点加入队列中{d[j]=d[t]+w[i];if(!st[j])//将没有在队列中的点加入队列中{q.push(j);st[j]=true;}}}}return d[n];
}
int main()
{memset(h,-1,sizeof(h));cin>>n>>m;for(int i=0;i<m;i++) {int a,b,c;cin>>a>>b>>c;add(a,b,c);}memset(d,0x3f,sizeof(d));int t=spfa();if(t==0x3f3f3f3f) puts("impossible");else printf("%d\n",t);return 0;
}

堆优化版的spfa算法

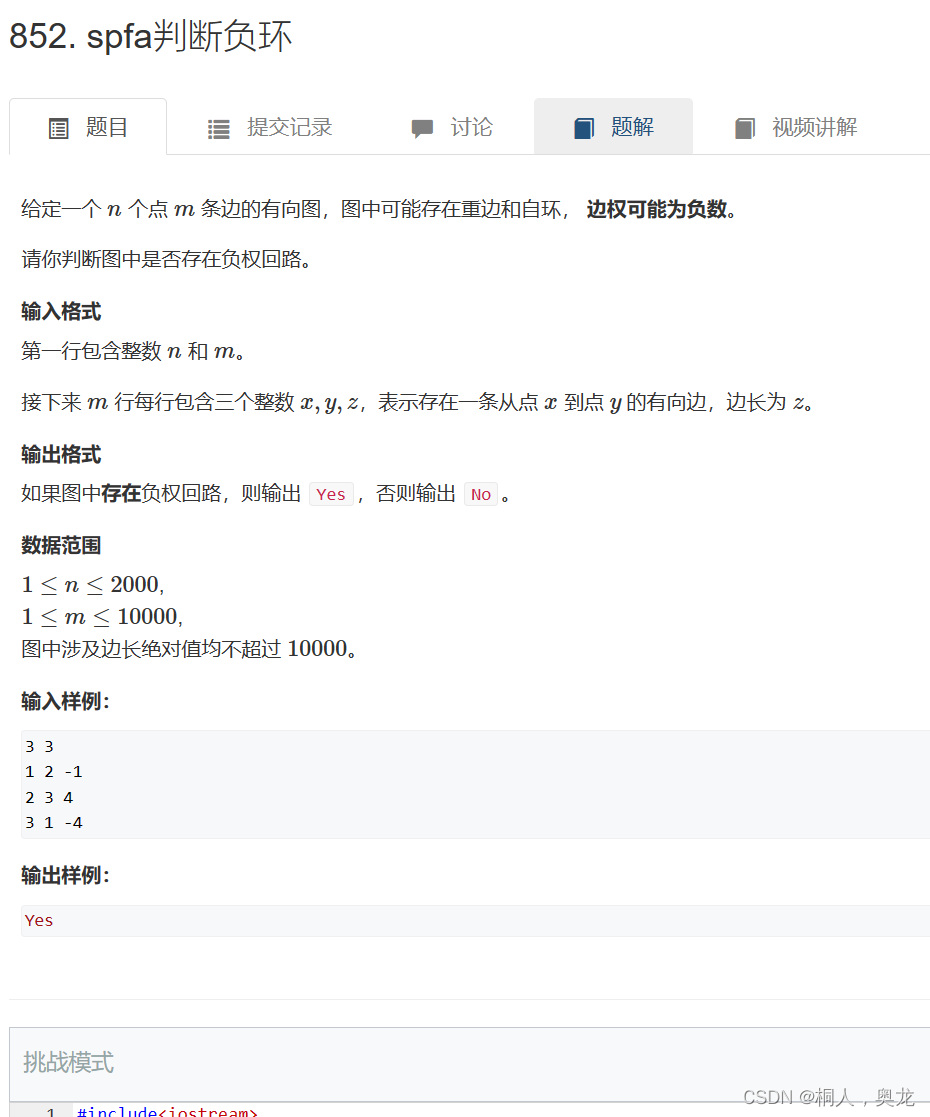
算法思想

spfa算法是bellman_fold算法的进化
判负环的基本方法是spfa
将数据读入，因为不知道那个点是负环的起点所有每个点都有可能–>将所有点加入队列，如果距离更小，更新距离并将此点加入队列

算法步骤以及实现

#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
const int N=1e4+10;
//d不需要进行初始化，如果存在负权边那么一定会改变
int d[N],st[N],w[N],h[N],e[N],ne[N],idx,cnt[N];
int n,m;void add(int a,int b,int c)
{e[idx]=b,ne[idx]=h[a],w[idx]=c,h[a]=idx++;
}
bool spfa()
{queue<int> q;for(int i=1;i<=n;i++) q.push(i),st[i]=true;while(q.size()){int t=q.front();q.pop();st[t]=false;for(int i=h[t];~i;i=ne[i]){int j=e[i];if(d[j]>d[t]+w[i]){d[j]=d[t]+w[i];cnt[j]=cnt[t]+1;//当点的个数大于等于n的时候，证明已经是出现负环了if(cnt[j]>=n) return true;if(!st[j]) {st[j]=true;q.push(j);}}}}return false;
}
int main()
{cin>>n>>m;memset(h,-1,sizeof(h));//memset(d,0x3f,sizeof(d));while(m--){int a,b,c;cin>>a>>b>>c;add(a,b,c);}if(spfa()) puts("Yes");else puts("No");return 0;
}

floyd算法—多源汇—不存在负权回路

算法思想

稠密图，使用邻接矩阵来存
因为是多源汇，所有每个点都可能使起点，所以在初始化的时候需要注意将每个点的自己到自己的距离初始化为0

算法步骤以及实现

#include<cstring>
#include<iostream>
using namespace std;
const int N=210,INF=0x3f3f3f3f;
int d[N][N];
int n,m,k;void floyd()
{for(int k=1;k<=n;k++)for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)d[i][j]=min(d[i][j],d[i][k]+d[k][j]);
}
int main()
{cin>>n>>m>>k;//多源汇for(int i=1;i<=n;i++)for(int j=1;j<=n;j++) if(i==j) d[i][j]=0;else d[i][j]=INF;while(m--){int a,b,c;cin>>a>>b>>c;d[a][b]=min(d[a][b],c);}floyd();while(k--){int a,b;cin>>a>>b;if(d[a][b]>INF/2) puts("impossible");else printf("%d\n",d[a][b]);}return 0;
}

以上是我的一些暂时的理解，可能有些不恰当的地方，
以后如果发现了更好的理解方式，会回来的。