平稳序列建模 #时间序列分析 #R语言-编程知识

掌握序列预测的主要内容，熟悉预测的步骤。
掌握平稳序列的步骤，能熟练运用R软件实现各个步骤。

训练数据在文末！！！

练习1、根据某城市过去63年中每年降雪量数据（行数据）（题目1数据.txt），求：

（1）通过序列时序图和单位根检验判断序列的平稳性，完成纯随机性检验；

（2）绘制序列的样本自相关图（ACF）和偏自相关图（PACF），根据相关性特征，选择合适模型拟合该序列的发展，并求出拟合模型的口径；

（3）对上述选定的拟合模型进行模型的检验；

（4）利用拟合模型预测该城市未来5年的降雪量，绘制预测图。

data <- scan("F:/时间序列分析/实验8/习题数据/1.txt")
x <- ts(data,start=1960)
plot(x) #时序图
#单位根检验
install.packages("aTSA")
library(aTSA)
adf.test(x)
#白噪声检验
for(i in 1:2) print(Box.test(x,type = "Ljung-Box",lag = 6*i))
#绘制自相关图和偏自相关图
par(mfrow = c(1,2))
acf(x)
pacf(x)#模型参数估计，确定模型的口径
x.fit1 <- arima(x,order = c(0,0,2),method = "ML")
#模型检验
ts.diag(x.fit1)
t = abs(x.fit1$coef)/sqrt(diag(x.fit1$var.coef))
pt(t,length(x)-length(x.fit1$coef),lower.tail = F)#预测
install.packages("forecast")
library(forecast)
fore1 <- forecast::forecast(x.fit1,h=5)
plot(fore1,lty=2)
lines(fore1$fitted,col=4)

结果分析：

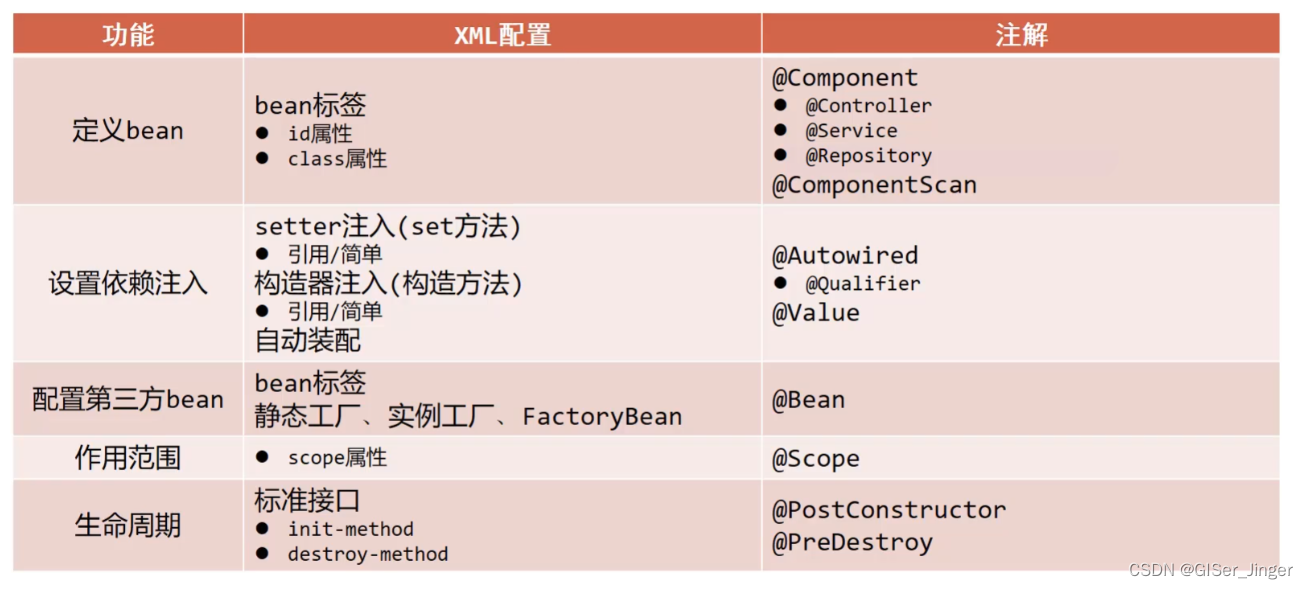
时序图：从时序图可以看出，该序列在常数80附近波动，且波动有界。认为该序列是平稳序列。

单位根检验：检验结果显示该序列可认为是平稳序列(带漂移项0-3阶滞后模型和既有漂移项又有趋势项的0-3阶滞后模型的P值小于0.05)。

Augmented Dickey-Fuller Test

alternative: stationary

Type 1: no drift no trend

     lag     ADF p.value

[1,]   0 -1.4009   0.175

[2,]   1 -0.6585   0.441

[3,]   2 -0.4331   0.517

[4,]   3 -0.0936   0.614

Type 2: with drift no trend

     lag   ADF p.value

[1,]   0 -5.72 0.0100

[2,]   1 -3.44 0.0153

[3,]   2 -3.34 0.0196

[4,]   3 -2.58 0.1050

Type 3: with drift and trend

     lag   ADF p.value

[1,]   0 -6.35 0.0100

[2,]   1 -4.04 0.0142

[3,]   2 -3.94 0.0181

[4,]   3 -3.09 0.1313

----

Note: in fact, p.value = 0.01 means p.value <= 0.01

白噪声检验：延迟12阶的LB统计量的P值大于α=0.05，但延迟6阶的LB统计量的P值小于α=0.05，则拒绝原假设，认为序列是非白噪声序列。

Box-Ljung test

data: x

X-squared = 13.284, df = 6, p-value = 0.03874

Box-Ljung test

data: x

X-squared = 14.893, df = 12, p-value = 0.2474

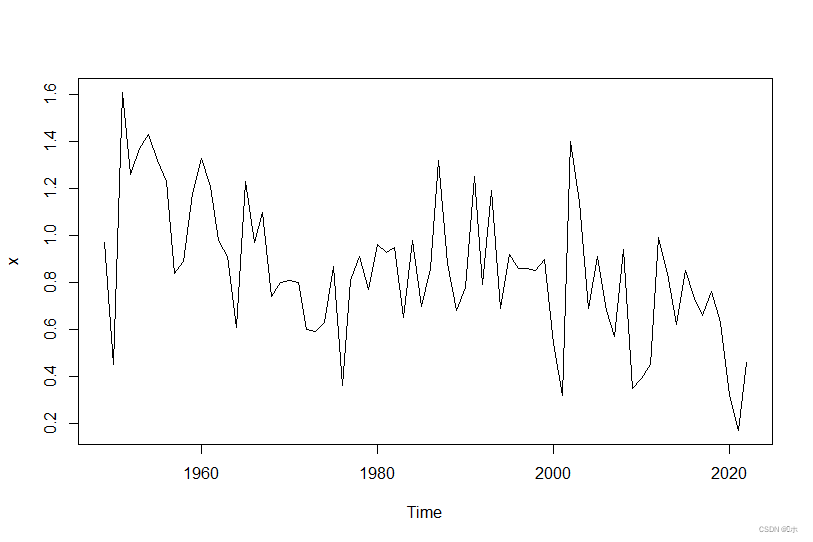
ACF和PACF图：

从自相关图看出，自相关系数呈现出不规则地衰减到零值附近。判定为拖尾；。判定拖尾；
从偏自相关图看出，只有1阶自相关系数在2倍标准差范围之外，之后几乎95%的自相关系数都突然衰减到2倍标准差范围之内。判定为1阶截尾；

综上所述，序列呈现出自相关系数2阶截尾的特性，偏自相关系数拖尾的特性，初步确定拟合模型为AR(1)模型。

AR(1)模型口径： $x_{t}-80.8793=\frac{\varepsilon _{t}}{1-0.3302B}$ ， $Var(\varepsilon _{t})=496.8$

该模型的等价表达为：

$x_{t}=54.17296+0.3302x_{t-1}+\varepsilon _{t}$ ， $Var(\varepsilon _{t})=496.8$

arima(x = x, order = c(1, 0, 0), method = "ML")

Coefficients:

         ar1 intercept

      0.3302    80.8793

s.e. 0.1236     4.1723

sigma^2 estimated as 496.8: log likelihood = -285.01, aic = 576.01

模型检验：

模型显著性检验：因为4-24阶延迟下LB统计量的P值都显著大于0.05，接受原假设，可以认为该拟合模型的残差序列属于白噪声序列，即该拟合模型显著有效。残差Q-Q图显示，数据点基本围绕在基准线附近，不能拒绝残差项是正态的假设。

模型参数显著性检验：t统计量的P值小于α＝0.05，拒绝原假设，故认为三个参数均显著非零。

ma1 ma2 intercept

1.117473e-02 5.393214e-03 4.366319e-27

（4）未来5年的降雪量的预测结果：

Point Forecast Lo 80 Hi 80 Lo 95 Hi 95

2023       86.17761 58.46671 113.8885 43.79744 128.5578

2024       85.90287 56.99458 114.8112 41.69146 130.1143

2025       80.89902 50.82791 110.9701 34.90923 126.8888

2026       80.89902 50.82791 110.9701 34.90923 126.8888

2027       80.89902 50.82791 110.9701 34.90923 126.8888

预测图：

图中：虚线为观察值，实线为拟合值，深色阴影部分为置信水平为80%的预测置信区间，浅色阴影部分为置信水平为95%的预测值置信区间。

练习2、根据某地区连续74年的谷物产量（行数据）（题目2数据.txt），求：

（1）通过序列时序图和单位根检验判断序列的平稳性，完成纯随机性检验；

（2）绘制序列的样本自相关图（ACF）和偏自相关图（PACF），根据相关性特征，选择合适模型拟合该序列的发展，并求出拟合模型的口径；

（3）对上述选定的拟合模型进行模型的检验；

（4）利用拟合模型预测该地区未来5年的谷物产量，绘制预测图。

data <- scan("F:/时间序列分析/实验8/习题数据/2.txt")
x <- ts(data,start=1949)
plot(x) #时序图
#单位根检验
install.packages("aTSA")
library(aTSA)
adf.test(x)
#白噪声检验
for(i in 1:2) print(Box.test(x,type = "Ljung-Box",lag = 6*i))
#绘制自相关图和偏自相关图
par(mfrow = c(1,2))
acf(x)
pacf(x)
#模型参数估计，确定模型的口径
x.fit1 <- arima(x,order = c(1,0,0),method = "ML")
#模型检验
ts.diag(x.fit1)
t = abs(x.fit1$coef)/sqrt(diag(x.fit1$var.coef))
pt(t,length(x)-length(x.fit1$coef),lower.tail = F)
#预测
install.packages("forecast")
library(forecast)
fore1 <- forecast::forecast(x.fit1,h=5)
plot(fore1,lty=2)
lines(fore1$fitted,col=4)

结果分析：

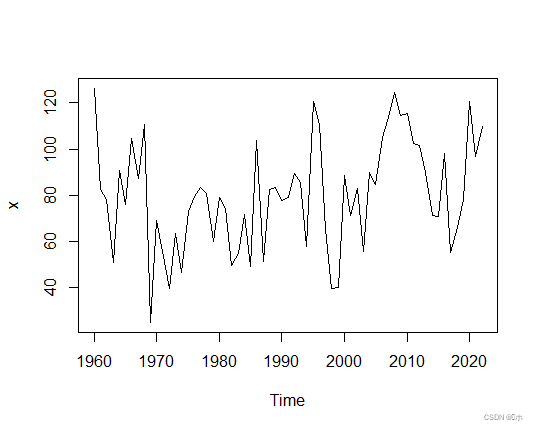
时序图：从时序图可以看出，该序列在常数0.8附近波动，且波动有界。认为该序列是平稳序列。

单位根检验：检验结果显示该序列可认为是平稳序列(无漂移项0阶滞后模型，带漂移项0-1阶滞后模型和既有漂移项又有趋势项的0-2阶滞后模型的P值小于0.05)。

Augmented Dickey-Fuller Test

alternative: stationary

Type 1: no drift no trend

     lag   ADF p.value

[1,]   0 -1.73   0.083

[2,]   1 -1.03   0.307

[3,]   2 -1.25   0.227

[4,]   3 -1.25   0.227

Type 2: with drift no trend

     lag   ADF p.value

[1,]   0 -5.62 0.0100

[2,]   1 -3.66 0.0100

[3,]   2 -2.68 0.0864

[4,]   3 -2.12 0.2831

Type 3: with drift and trend

     lag   ADF p.value

[1,]   0 -7.12 0.0100

[2,]   1 -5.56 0.0100

[3,]   2 -3.98 0.0157

[4,]   3 -3.32 0.0750

----

Note: in fact, p.value = 0.01 means p.value <= 0.01

白噪声检验：延迟6阶和延迟12阶的LB统计量的P值均小于α=0.05，则拒绝原假设，认为序列是非白噪声序列。

Box-Ljung test

data: x

X-squared = 29.872, df = 6, p-value = 4.156e-05

Box-Ljung test

data: x

X-squared = 38.58, df = 12, p-value = 0.0001234

ACF图和PACF图：

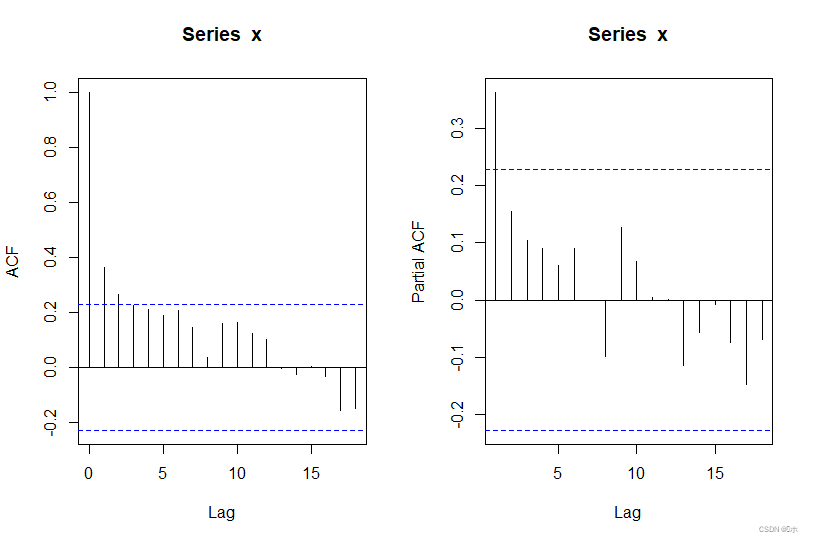
从自相关图看出，自相关系数呈现出“坐着滑梯落水”缓慢收敛到零值附近。判定为拖尾特性；
从偏自相关图看出，只有1阶偏自相关系数在2倍标准差范围之外，之后几乎95%的自相关系数都突然衰减到2倍标准差范围之内。判定为1阶截尾；；

综上所述，序列呈现出自相关系数拖尾的特性，偏自相关系数1阶截尾的特性，初步确定拟合模型为AR(1)模型。

AR(1)模型口径： $x_{t}-0.8491=\frac{\varepsilon _{t}}{1-0.3681B}$ ， $Var(\varepsilon _{t})=0.07467$

该模型的等价表达为： $x_{t}=0.5365463+0.3681x_{t-1}+\varepsilon_{t}$ ， $Var(\varepsilon _{t})=0.07467$

arima(x = x, order = c(1, 0, 0), method = "ML")

Coefficients:

         ar1 intercept

      0.3681     0.8491

s.e. 0.1085     0.0499

sigma^2 estimated as 0.07467: log likelihood = -9.07, aic = 24.14

模型检验：

模型参数显著性检验：t统计量的P值小于α＝0.05，拒绝原假设，故认为两个参数均显著非零。

ar1 intercept

5.637834e-04 3.037430e-27

预测该地区未来5年的谷物产量：

Point Forecast Lo 80 Hi 80 Lo 95 Hi 95

2023      0.7058602 0.3556749 1.056046 0.1702980 1.241422

2024      0.7963705 0.4232095 1.169532 0.2256700 1.367071

2025      0.8296908 0.4535239 1.205858 0.2543932 1.404988

2026      0.8419572 0.4653848 1.218530 0.2660394 1.417875

2027      0.8464730 0.4698456 1.223100 0.2704712 1.422475

预测图：