分类损失函数与评估指标-编程知识

1 评估指标

1.1 准确率

1.2 精确率

1.3 召回率

1.4 F1 score

1.5 ROC曲线

1.6 AUC

1.7 PRC曲线的优势

2 损失函数

1. 负对数似然损失

2. 交叉熵损失

3. 指数损失

3 分类问题为什么用交叉熵损失不用 MSE 损失

1 评估指标

混淆矩阵

TP(True Positive) ---- 正确预测正类的样本（真阳性）
FN(False Negative) ---- 错误预测为负类的样本（假阴性）
FP(False Positive) ---- 错误的预测为正类（假阳性）
TN(True Negative) ---- 正确预测为负类（真阴性）

1.1 准确率

准确率(accuracy): 反映分类器统对整个样本的判定能力，能将正的判定为正，负的判定为负，公式如下：

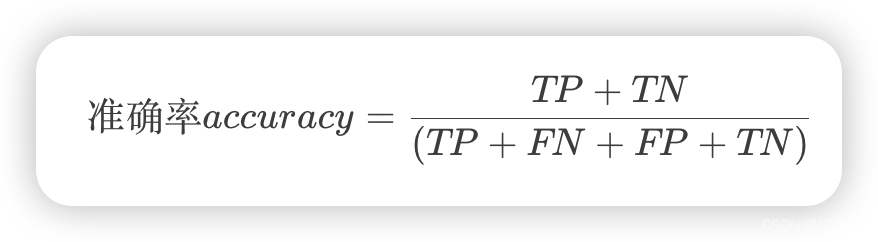
1.2 `精确率`

精确率(Precision)：指的是所得数值与真实值之间的精确程度；预测正确的正例数占模型预测为正例总量的比率，一般情况下，精确率越高，说明模型的效果越好。

1.3 `召回率`

召回率(Recall)：预测对的正例数占所有正例的比率，一般情况下，Recall越高，说明有更多的正类样本被模型预测正确，模型的效果越好。

`1.4 F1 score`

F1是精确率和召回率的调和均值，即：

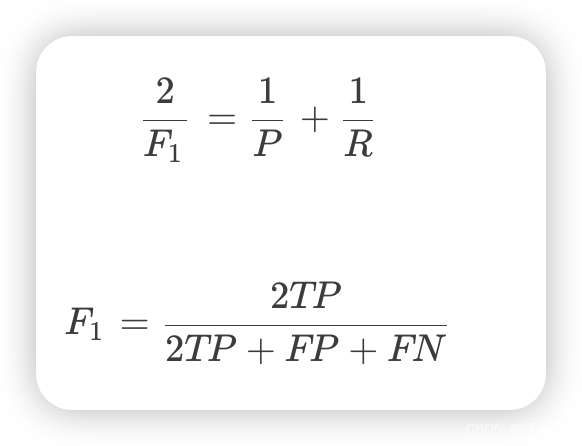
1.5 ROC曲线

每次选取一个不同的threshold，我们就可以得到一组FPR和TPR，即ROC曲线上的一点。

ROC曲线为 FPR 与 TPR 之间的关系曲线，这个组合以 FPR 对 TPR，即是以代价 (costs) 对收益 (benefits)，显然收益越高，代价越低，模型的性能就越好。

FPR：错误预测为正类的样本；

TRP：正确预测为正类的样本；

1.6 AUC

AUC的物理意义：正样本的预测结果大于负样本的预测结果的概率。所以AUC反映的是分类器对样本的排序能力。

AUC 值为 ROC 曲线所覆盖的区域面积，显然，AUC越大，分类器分类效果越好。

AUC = 1，是完美分类器。

0.5 < AUC < 1，优于随机猜测。有预测价值。

AUC = 0.5，跟随机猜测一样（例：丢铜板），没有预测价值。

AUC < 0.5，比随机猜测还差；但只要总是反预测而行，就优于随机猜测。

注：对于AUC小于 0.5 的模型，我们可以考虑取反（模型预测为positive，那我们就取negtive），这样就可以保证模型的性能不可能比随机猜测差。

1.7 PRC曲线的优势

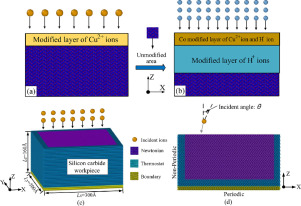
在正负样本分布得极不均匀(highly skewed datasets)，负例远大于正例时，并且这正是该问题正常的样本分布时，PRC比ROC能更有效地反应分类器的好坏，即PRC曲线在正负样本比例悬殊较大时更能反映分类的真实性能。例如上面的(c)(d)中正负样本比例为1:10，ROC效果依然看似很好，但是PR曲线则表现的比较差。举个例子，

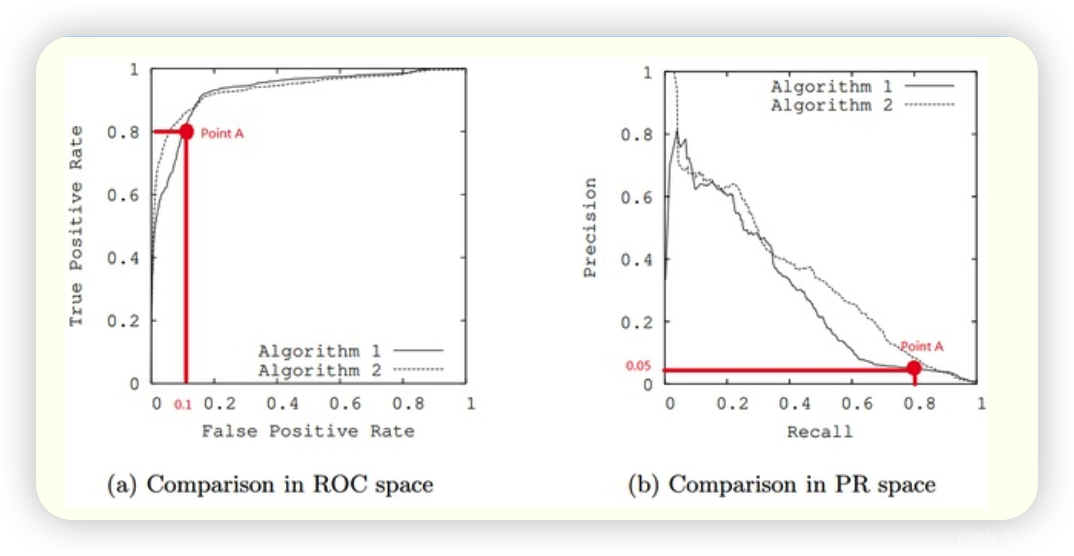
单从图（a）看，这两个分类器都比较完美(非常接近左上角)。而从图（b）可以看出，这两个分类器仍有巨大的提升空间。那么原因是什么呢？通过看Algorithm1的点 A，可以得出一些结论。首先图（a）和（b中）的点A是相同的点，因为TPR就是Recall，两者是一样的。

　　假设数据集有100个正样本。可以得到以下结论：

　　由图（a）点A，可得：TPR=TP/(TP+FN)=TP/所有正样本 =TP/100=0.8，所以TP=80。

　　由图（b）点A，可得：Precision=TP/(TP+FP)=80/(80+FP)=0.05，所以FP=1520。

　　再由图（a）点A，可得：FPR=FP/(FP+TN)=FP/所有负样本=1520/所有负样本=0.1，所以负样本数量是15200。

　　由此，可以得出原数据集中只有100个正样本，却有15200个负样本！这就是极不均匀的数据集。直观地说，在点A处，分类器将1600 (1520+80)个样本预测为positive，而其中实际上只有80个是真正的positive。我们凭直觉来看，其实这个分类器并不好。但由于真正negative instances的数量远远大约positive，ROC的结果却“看上去很美”，因为这时FPR因为负例基数大的缘故依然很小。所以，在这种情况下，PRC更能体现本质。

PRC 曲线展示了在不同阈值下模型的精确率和召回率之间的权衡关系。一般来说，PRC 曲线越靠近右上角（精确率高、召回率高），表示模型性能越好。与 ROC 曲线相比，PRC 曲线更适用于处理类别不平衡的情况，因为它更加关注正例（少数类）的精确率和召回率。

在评估分类模型时，除了查看 PRC 曲线外，还可以计算曲线下面积（Area Under the PRC Curve，AUPRC）来 quantitatively 衡量模型性能。AUPRC 值越接近 1，表示模型性能越好。