第1关:预测句子概率
任务描述
本关任务:利用二元语言模型计算句子的概率
相关知识
为了完成本关任务,你需要掌握:1.条件概率计算方式。 2.二元语言模型相关知识。
条件概率计算公式
条件概率是指事件A在事件B发生的条件下发生的概率。条件概率表示为:P(A|B)。若只有两个事件A,B,则有如下公式:
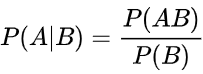
二元语言模型
二元语言模型也称为一节马尔科夫链,通俗的讲,我们可以认为这是一个词的概率实际上只是跟前边的词有关,那么就可以有以下的方程:
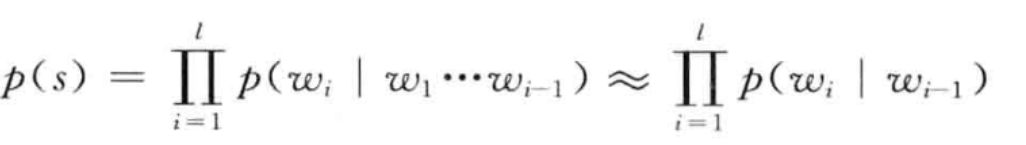
同时为了保证条件概率在 i=1 时有意义,同时为了保证句子内所有字符串的概率和为 1,可以在句子首尾两端增加两个标志: <BOS \W1W2…Wn\ EOS> 为了估计P(WI|WI-1)的条件概率,我们计算出wi-1,wi的词汇出此案的频率然后进行归一化,公式如下:
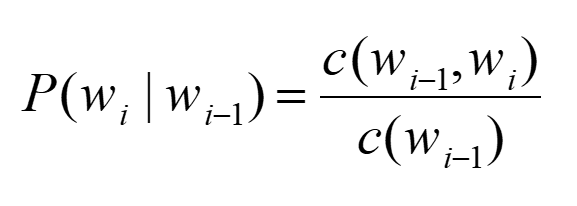
计算出每个词汇的概率后,便可根据公式求得句子的概率。
编程要求
根据提示,在右侧编辑器补充代码,计算并输出测试语句的概率
测试说明
平台会对你编写的代码进行测试: 语料库:
研究生物很有意思。他大学时代是研究生物的。生物专业是他的首选目标。他是研究生。
测试输入:
研究生物专业是他的首选目标
预期输出:
0.004629629629629629
import jiebajieba.setLogLevel(jieba.logging.INFO)# 将句子变为"BOSxxxxxEOS"这种形式
def reform(sentence):if sentence.endswith("。"):sentence = sentence[:-1]sentence = sentence.replace("。", "EOSBOS")sentence = "BOS" + sentence + "EOS"return sentence# 分词并统计词频
def segmentation(sentence, dic):jieba.suggest_freq("BOS", True)jieba.suggest_freq("EOS", True) # 让jieba库知道"BOS"和"EOS"这两个词的存在,并记录它们的出现频率lists = jieba.lcut(sentence, HMM=False) # 当输入的文本比较短时,隐马尔科夫模型的效果可能会下降,导致分词结果不准确if dic is not None:for word in lists:if word not in dic:dic[word] = 1else:dic[word] += 1return lists# 比较两个数列,二元语法
def compareList(ori_list, tes_list):count_list = [0] * len(tes_list)for t in range(len(tes_list)-1):for n in range(len(ori_list)-1):if tes_list[t] == ori_list[n]:if tes_list[t+1] == ori_list[n+1]:count_list[t] += 1return count_list # 计算概率
def probability(tes_list, ori_dic, count_list):flag = 0p = 1del tes_list[-1]for key in tes_list:p *= float(count_list[flag]) / float(ori_dic[key])flag += 1return pif __name__ == "__main__":# 语料句子sentence_ori = "研究生物很有意思。他大学时代是研究生物的。生物专业是他的首选目标。他是研究生。"ori_dict = {}# 测试句子sentence_test = input()ori_dict2 = {}sentence_ori_temp = reform(sentence_ori)ori_list = segmentation(sentence_ori_temp, ori_dict)sentence_tes_temp = reform(sentence_test)tes_list = segmentation(sentence_tes_temp, None)count_list = compareList(ori_list, tes_list)p = probability(tes_list, ori_dict, count_list)print(p)第2关:数据平滑
任务描述
本关任务:实现二元语言模型的数据平滑,并利用平滑后的数据计算句子概率。
相关知识
为了完成本关任务,你需要掌握:1.模型平滑化。2.good-turning平滑。
模型平滑
在使用语言模型直接计算某个句子出现的概率时,可能会由于某个单词或单词对出现的概率为0而导致整个句子出现的概率为0。 例如下面这个场景:
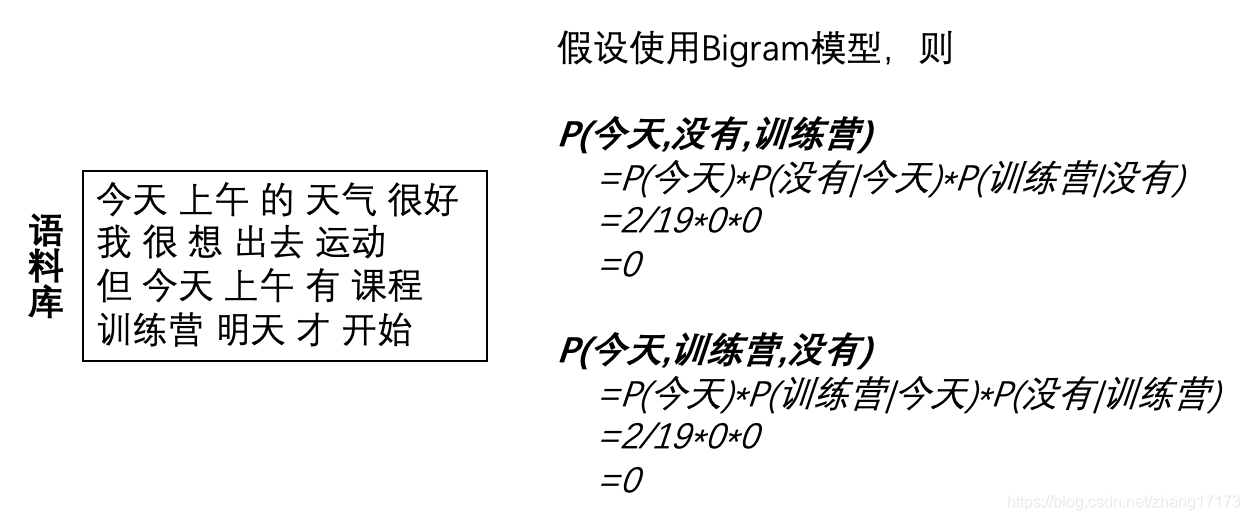
在上面的场景中,由于部分单词对出现的概率为0,导致最终两句话出现的概率均为0。但实际上,s1=“今天没有训练营”比s2=“今天训练营没有”更符合语法习惯,我们也更希望计算出来的P(s1)大于P(s2)。 一般来说,语言模型的平滑处理可分为以下三类:
- Discounting(折扣):通过给概率不为0的项打折扣,来提高概率为0的项的概率;
- Interpolation(插值):在使用N-gram模型计算某一项的概率时,同时结合低阶的模型所计算出的概率;
- Back‐off:approximate counts of unobserved N‐gram based on the proportion of back‐off events (e.g., N‐1 gram)。
这里我们主要介绍与使用Discounting中的good-turning平滑方法。
good-turning平滑
Good-Turing技术是在1953年由古德(I.J.Good)引用图灵(Turing)的方法而提出来的,其基本思想是:用观察计数较高的N元语法数重新估计概率量的大小,并把它指派给那些具有零计数或者较低计数的N元语法。涉及的符号含义为:
c:某个N元语法出现的频数。
Nc:出现次数为c的 N-gram 词组的个数,是频数的频数
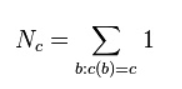
c*:Good-Turing平滑计数
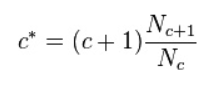
设N为测试元组集合中元组的数目,则有如下公式:
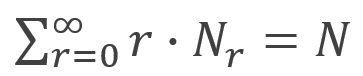
通过新频数可计算出经过good-turing平滑后的元组概率,公式如下:
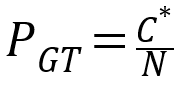
编程要求
根据提示,在右侧编辑器补充代码,编写平滑函数,计算句子的概率
测试说明
平台会对你编写的代码进行测试:
语料库:
研究生物很有意思。他大学时代是研究生物的。生物专业是他的首选目标。他是研究生。
测试输入:
他是研究物理的
预期输出:
5.6888888888888895e-05
import jieba
#语料句子
sentence_ori="研究生物很有意思。他大学时代是研究生物的。生物专业是他的首选目标。他是研究生。"
#测试句子
sentence_test=input()
#任务:编写平滑函数完成数据平滑,利用平滑数据完成对2-gram模型的建立,计算测试句子概率并输出结果
# ********** Begin *********#
def gt(N, c):if c+1 not in N:cx = c+1else:cx = (c+1) * N[c+1]/N[c]return cx
jieba.setLogLevel(jieba.logging.INFO)
sentence_ori = sentence_ori[:-1]
words = jieba.lcut(sentence_ori)
words.insert(0, "BOS")
words.append("EOS")
i = 0
lengh = len(words)
while i < lengh:if words[i] == "。":words[i] = "BOS"words.insert(i, "EOS")i += 1lengh += 1i += 1
phrases = []
for i in range(len(words)-1):phrases.append(words[i]+words[i+1])
phrasedict = {}
for phrase in phrases:if phrase not in phrasedict:phrasedict[phrase] = 1else:phrasedict[phrase] += 1
words_test = jieba.lcut(sentence_test)
words_test.insert(0, "BOS")
words_test.append("EOS")
phrases_test = []
for i in range(len(words_test)-1):phrases_test.append(words_test[i]+words_test[i+1])
pdict = {}
for phrase in phrases_test:if phrase not in phrasedict:pdict[phrase] = 0else:pdict[phrase] = phrasedict[phrase]
N = {}
for i in pdict:if pdict[i] not in N:N[pdict[i]] = 1else:N[pdict[i]] += 1
N[0] += 1
Nnum = 0
for i in N:Nnum += i*N[i]
p = 1
for phrase in phrases_test:c = pdict[phrase]cx = gt(N, c)p *= cx/Nnum
print(p)