素数判断:从O( n 2 n^2 n2)到O(n)学习之路
背景:每一个初学计算机的人肯定避免不了碰到素数,素数是什么,怎么判断?
素数的概念不难理解:素数即质数,指的是在大于1的自然数中,除了1和它本身不再有其他因数的自然数。
如何判断
刚进大学时,我最开始接触的就是最简单的那种,比较容易理解,但复杂度较高,容易超时
暴力写法
#include <iostream>
using namespace std;int primes[10000];
int main()
{int cnt = 0,n=1000;for (int i = 2; i < n; i++){int temp = 0;//假定是素数for (int j = 2; j < i; j++){if (i % j == 0) { temp = 1; break; }//只要i能整除j,那肯定不是质数,temp=1标记为合数}if (!temp)primes[cnt++] = i;}for (int i = 0; i < 20; i++)cout << primes[i] << " ";
}
时间复杂度:O( n 2 n^2 n2)
之后有看了网上的一些写法,学了些优化的方法
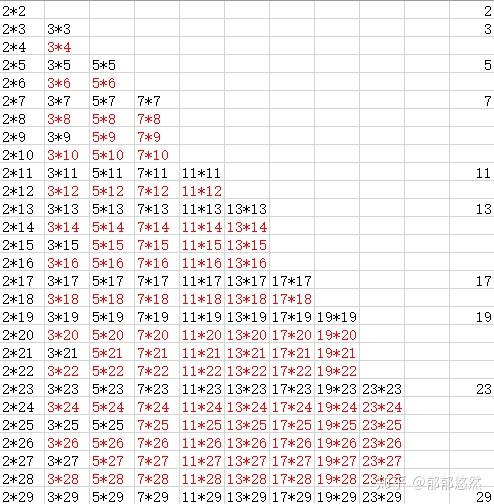
比如,我们判断到 n \sqrt n n 就可以结束了,为什么可以这样呢?
下面的这个图或许可以说明这一点

#include <iostream>
using namespace std;int primes[10000];
int main()
{int cnt = 0, n = 1000;for (int i = 2; i <n; i++){int temp = 0;//假定是素数if (i > 2 && i % 2 == 0)continue;//大于2的偶数肯定不是素数for (int j = 2; j*j<=i; j++)//这个地方可以写成j<=sqrt(i);但调用函数会慢一点//其次,写成乘法,而尽量不写j<=i/j;,乘法比除法更快{if (i % j == 0) { temp = 1; break; }//只要i能整除j,那肯定不是质数,temp=1标记为合数}if (!temp)primes[cnt++] = i;}for (int i = 0; i < 20; i++)cout << primes[i] << " ";
}
终极大法:欧拉线性筛
时间复杂度:O( n n n)
关于这方面的解释,我找了下知乎大佬的解释,我自己大概明白了基本原理,但并不能很好的阐述它
废话不多说,上图!!!




const int N=100000;
int primes[N];//质数表,是质数的加入其中
bool st[N];//false表示素数,true为非素数
void get_primes(int N)//利用线性筛找到2~n中的质数
{int cnt=0;st[0]=true;st[1]=true;//0和1为非素数for(int i=0;i<=N;i++){if(!st[i])primes[cnt++]=i;//如果没被筛掉,是质数,假如质数表for(int j=0;i*primes[j]<=N;j++){st[i*primes[j]]=true;//用最小质因子去筛素数if(i%primes[j]==0)break;}}
}
OK,让我们来道题试试吧
X的因子链
输入正整数$ X$,求 X X X 的大于 11 的因子组成的满足任意前一项都能整除后一项的严格递增序列的最大长度,以及满足最大长度的序列的个数。
输入格式
输入包含多组数据,每组数据占一行,包含一个正整数表示 X X X。
输出格式
对于每组数据,输出序列的最大长度以及满足最大长度的序列的个数。
每个结果占一行。
数据范围
1 ≤ X ≤ 2 20 1≤X≤2^{20} 1≤X≤220
输入样例:
2
3
4
10
100
输出样例:
1 1
1 1
2 1
2 2
4 6
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=(1<<20)+5;
int primes[N];bool st[N];
int minp[N];
void get_primes()//线性筛质数
{int cnt=0;for(int i=2;i<=N;i++){if(!st[i]){primes[cnt++]=i;minp[i]=i;}//记录最小质因数for(int j=0;primes[j]*i<=N;j++){st[primes[j]*i]=true;minp[primes[j]*i]=primes[j];//最小质因数if(i%primes[j]==0)break;}}
}
int main()
{ int x;get_primes();while(scanf("%d",&x)!=EOF){int k=0;int total=0;int sum[10]={0};//初始化数组while(x>1)//数的分解,用最小质因数去分解{ int t=minp[x];sum[k]=0;//我要用到的时候再重置为0,没用到的数据不为0没关系,因为遍历时数组只会遍历到k//而这k个数据在这里已经被重置后进行运算while(x%t==0){sum[k]++;total++;x/=t;}k++;}ll res=1;for(int i=2;i<=total;i++)res*=i;//总的阶乘for(int j=0;j<k;j++)for(int i=1;i<=sum[j];i++)res/=i;printf("%d %lld\n",total,res);memset(sum,0,sizeof(sum));//注意,这里开了memset会超时的,10^6的长度数组有100组数据就会运算10^8次了,容易超时} //当然,我们数组开到10然后重置是不会超时的,return 0;
}






![[Qt网络编程]之UDP通讯的简单编程实现](https://img-blog.csdnimg.cn/direct/83cc742e09474071862b6b8db63aa3b6.png)