2023牛客暑期多校训练营8-I Make It Square
https://ac.nowcoder.com/acm/contest/57362/I
文章目录
- 2023牛客暑期多校训练营8-I Make It Square
- 题意
- 解题思路
- 代码实现
题意

解题思路
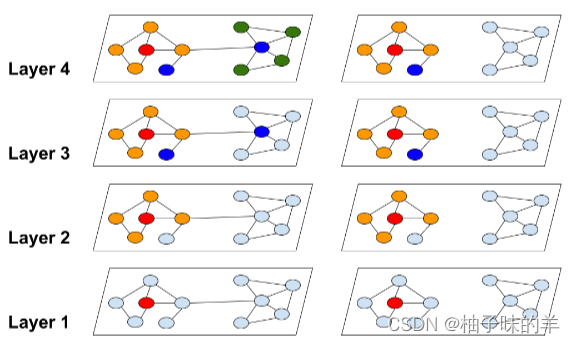
这里有两种情况,即 ∣ s ∣ > ∣ t ∣ |s|>|t| ∣s∣>∣t∣和 ∣ s ∣ < ∣ t ∣ |s|<|t| ∣s∣<∣t∣,首先考虑 ∣ s ∣ > ∣ t ∣ |s|>|t| ∣s∣>∣t∣的情况,对于不同的 m m m,有两种情况,用图画来表示下面两种情况:

显然对于每一种情况都要判断 t t t是否与 s 1 s_1 s1的后缀相同。否则答案必为 0 0 0。
如图,对于第一种情况,即 p p p与 q q q有重叠,设重叠部分有 k k k个元素,其答案显然为 2 6 k 26^k 26k;
对于第二种情况,还需要判断 s 2 s_2 s2与 s 1 s_1 s1的重叠部分是否相同。
判断 s 2 s_2 s2与 s 1 s_1 s1的重叠部分相同不需要一一枚举,可以发现,重叠部分即是 s s s的相同的前缀与后缀,可以用 k m p kmp kmp算法中的求 n e x t next next数组的方法来求。
而对于 ∣ s ∣ < ∣ t ∣ |s|<|t| ∣s∣<∣t∣,可以发现若交换 t t t与 s s s,不会影响最终答案,如下图:

左图中,上下 s s s对应的 t t t的区域距 t t t尾部都是 p / q p/q p/q,右图中,上下 s s s对应的 t t t的区域距 t t t头部都是 t 1 − t 2 / q 1 t_1-t_2/q_1 t1−t2/q1,显然 t 2 = q 2 t_2=q_2 t2=q2所以 s s s所对的区域都相同, s s s显然相同,所以交换后 1 1 1还是 1 1 1, 0 0 0还是 0 0 0, 2 6 k 26^k 26k还是 2 6 k 26^k 26k。
代码实现
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5,mod=998244353;
int m,nx[N];
long long ans[N];
char a[N],b[N];
int main(){cin>>m;scanf("%s %s",a+1,b+1);int A=strlen(a+1),B=strlen(b+1);if((A+B)%2){for(int i=1;i<=m;i++)cout<<0<<' ';return 0;}if(A<B)swap(a,b),swap(A,B);int k=0,f=0;nx[1]=0;for(int i=2;i<=A;i++){while(k>0&&a[k+1]!=a[i])k=nx[k];if(a[k+1]==a[i])k++;nx[i]=k;}int d=(A+B)/2,r=A-d;for(int i=1;i<=B;i++){if(b[i]!=a[d-B+i]){for(int i=1;i<=m;i++)cout<<0<<' ';return 0;}}f=nx[A];while(f>0){if(f<r)ans[r-f]=1;f=nx[f];}ans[r]=1;for(int i=r+1;i<=m;i++)ans[i]=ans[i-1]*26%mod;for(int i=1;i<=m;i++)cout<<ans[i]<<' ';
}