1.1 概述

二进制的优点


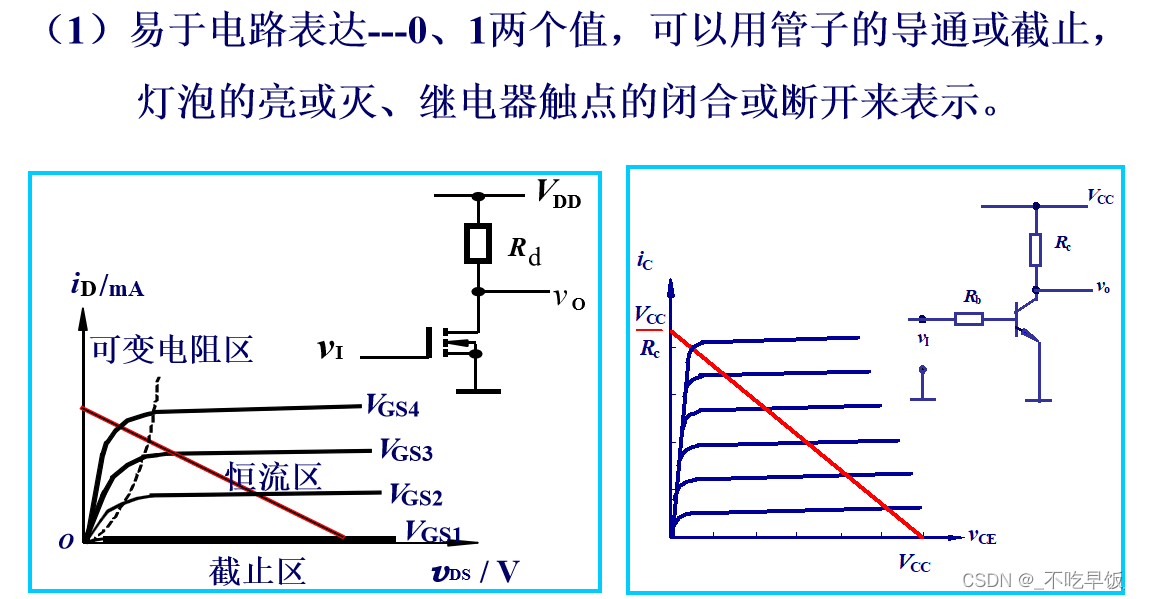
二进制的缺点

1.2 几种常用的数制

1.2.1 十进制（Decimal）

1.2.2 二进制（Binary）

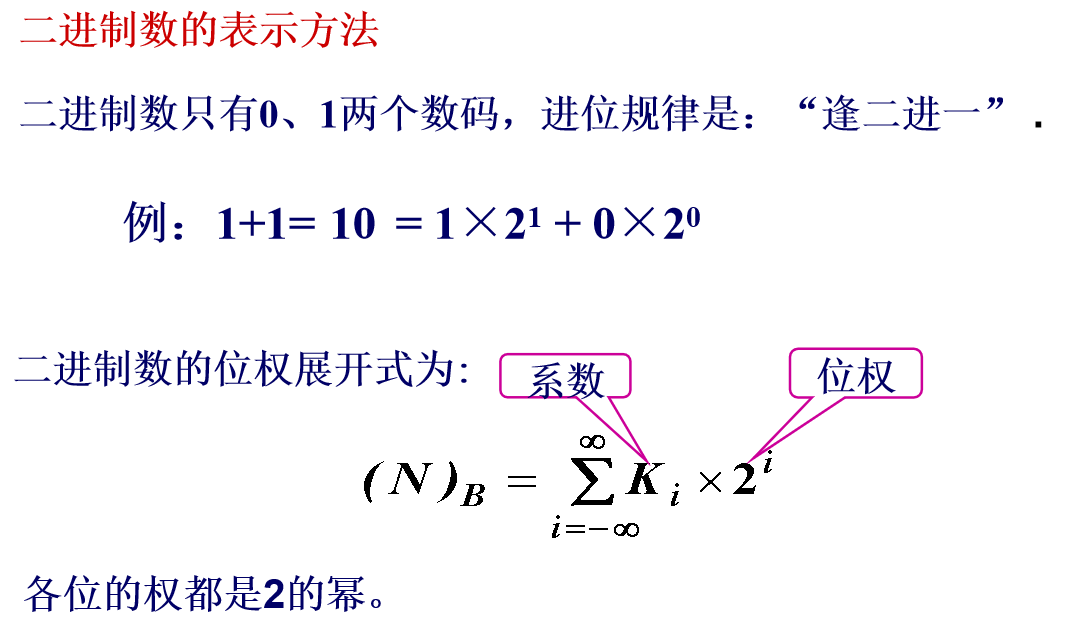
1.2.3 二-十进制之间的转换

1.2.4 十六进制和八进制

1. 十六进制（Hexadecimal）

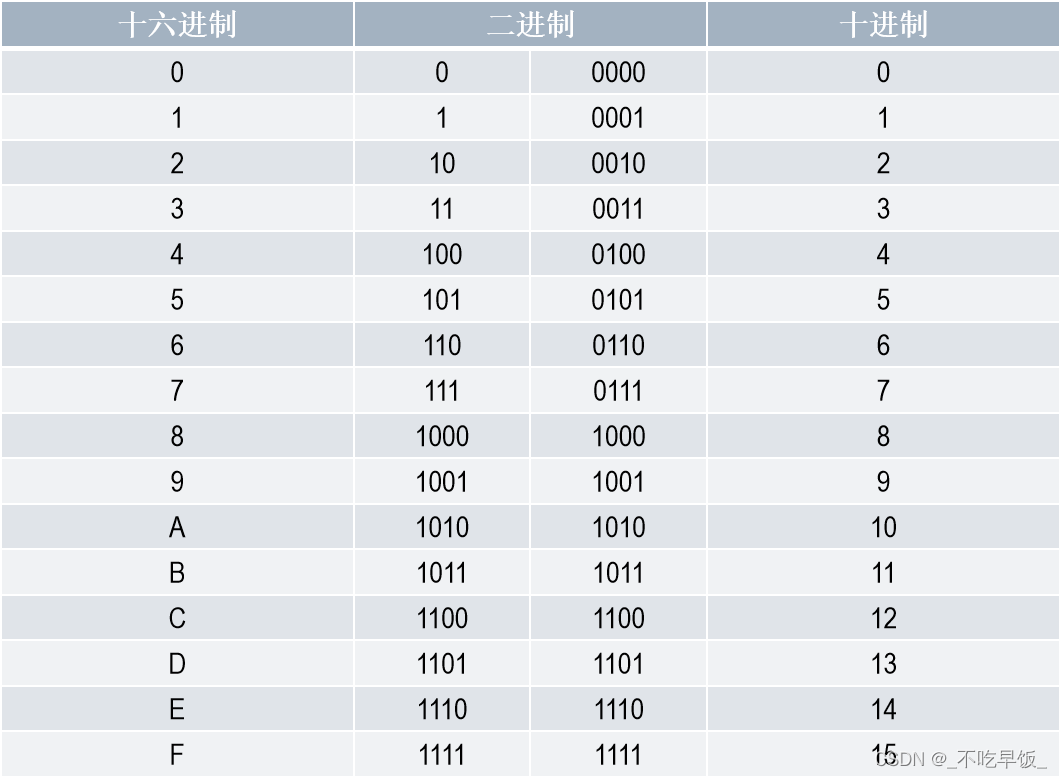
2. 八进制（Octal）

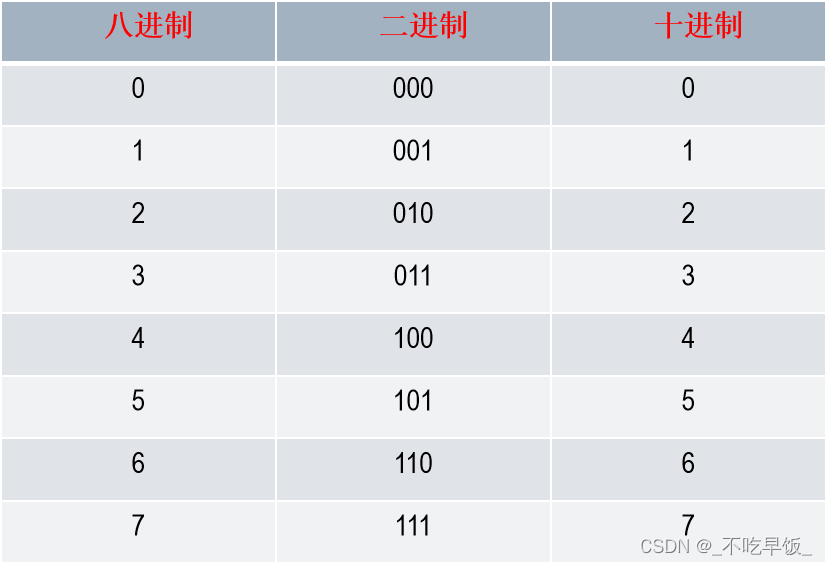
1.2.5 任意进制之间的转换

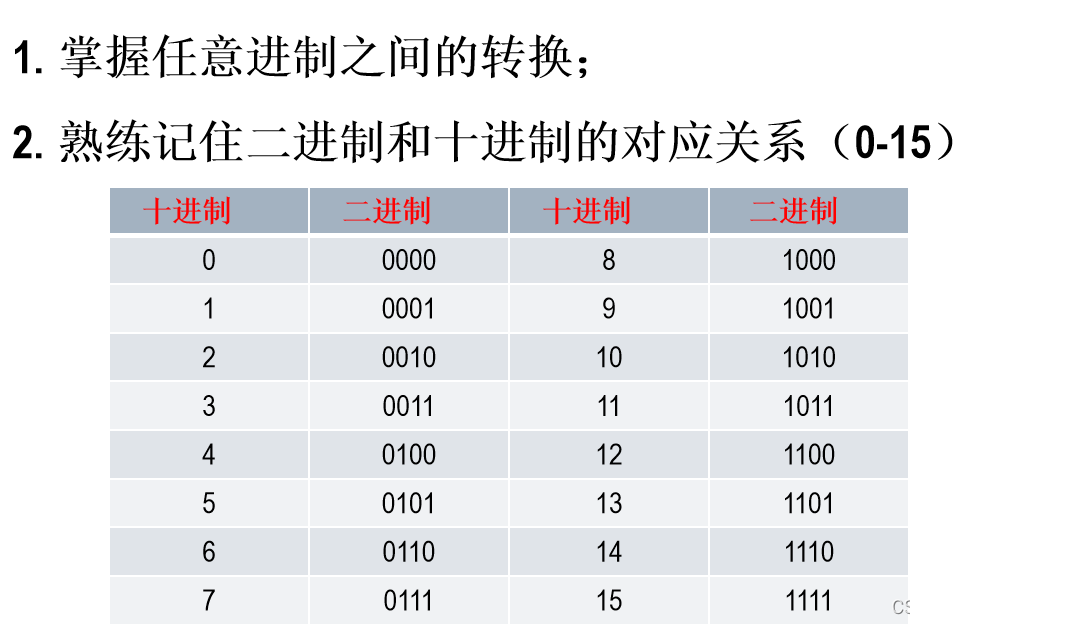
1.3 二进制代码

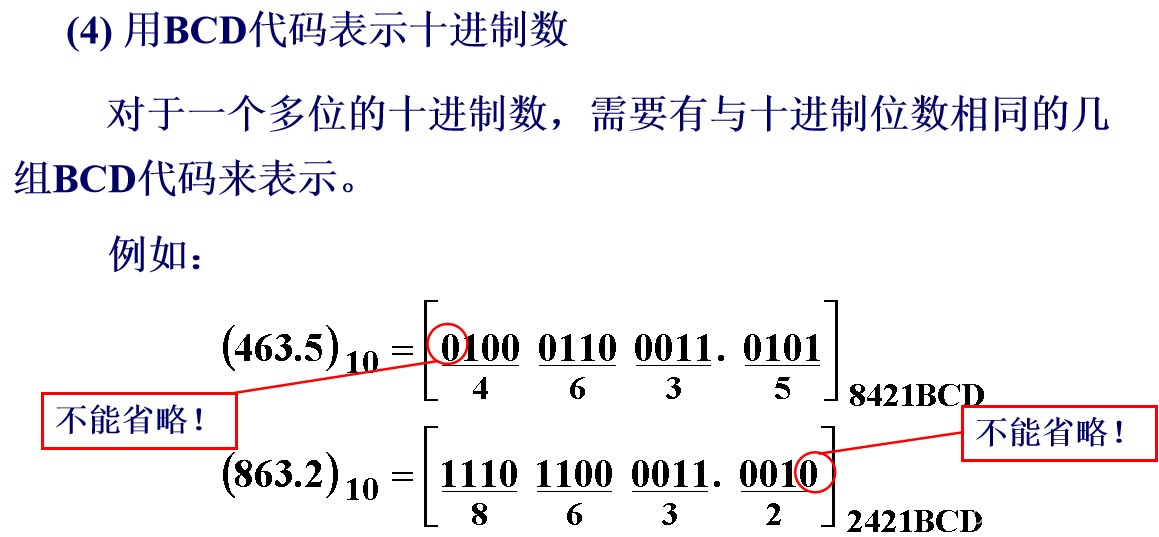
1.3.1 二-十进制码(BCD Binary Coded Decimal)

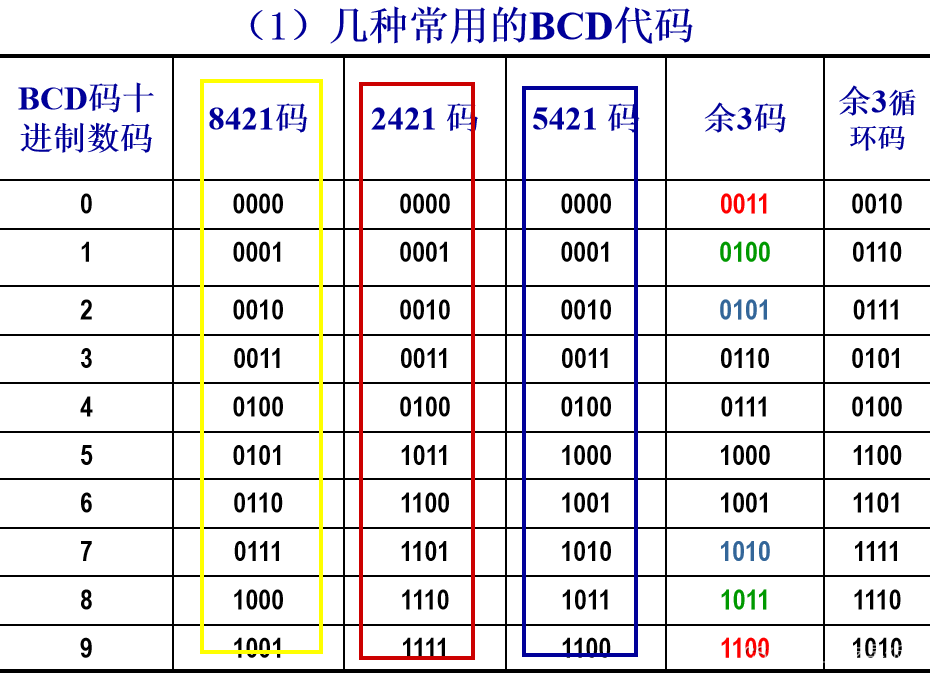
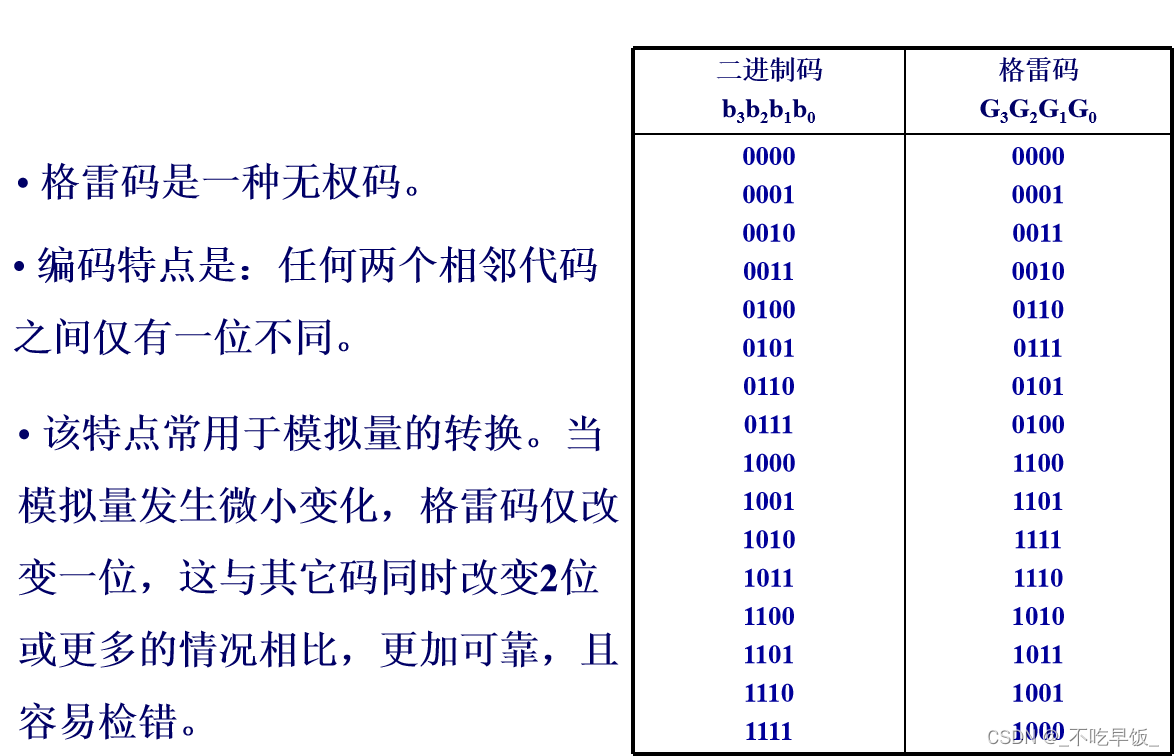
1.3.2 格雷码

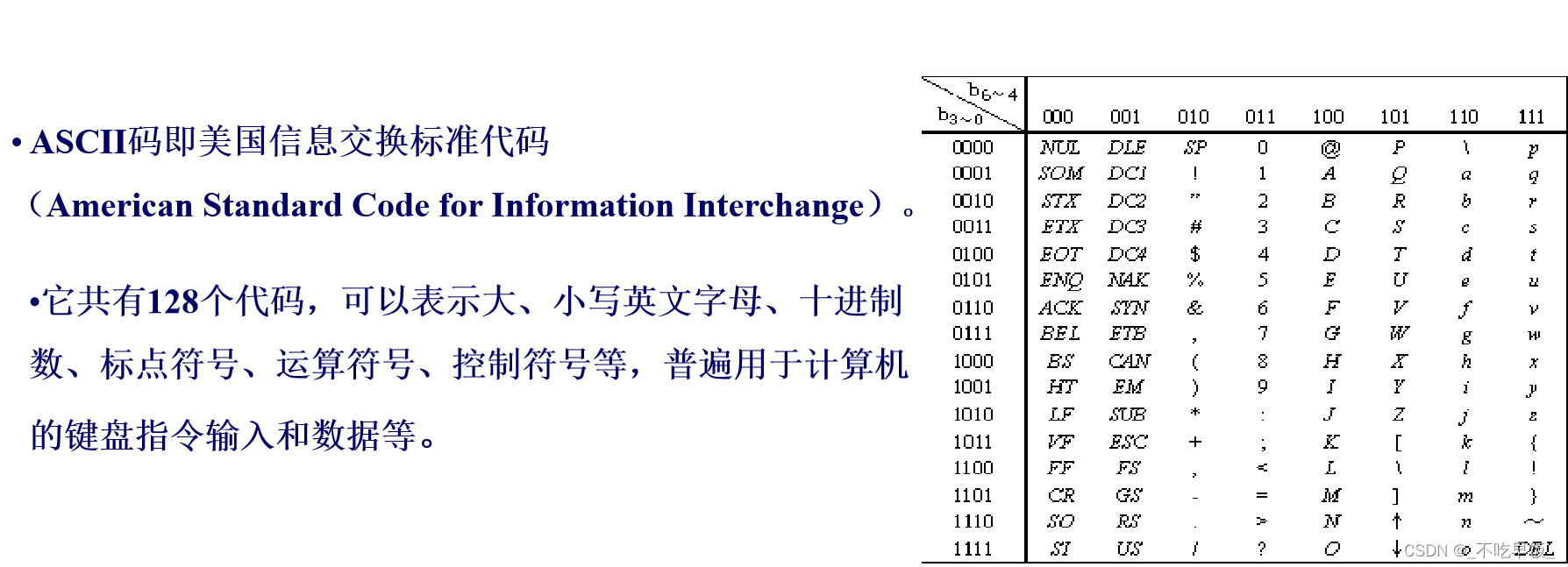
1.3.3 ASCII码

1.4 二进制数的算术运算

1.4.1 实现方法

运算规则：
1. 和十进制的运算规则类似
2. 逢二进一
指导思想：
1. 受限于元器件的状态和数量，尽量简化电路；
2. 充分利用二进制数的规律，发挥其优势。

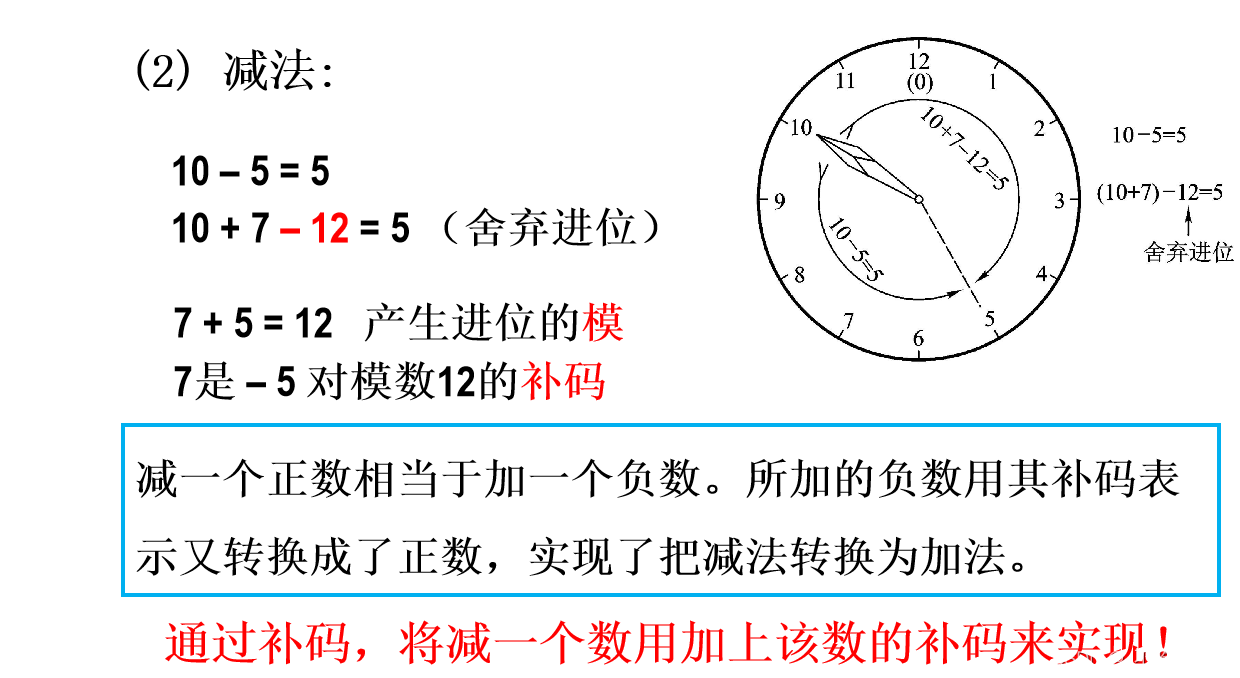
1.4.2 如何求补码

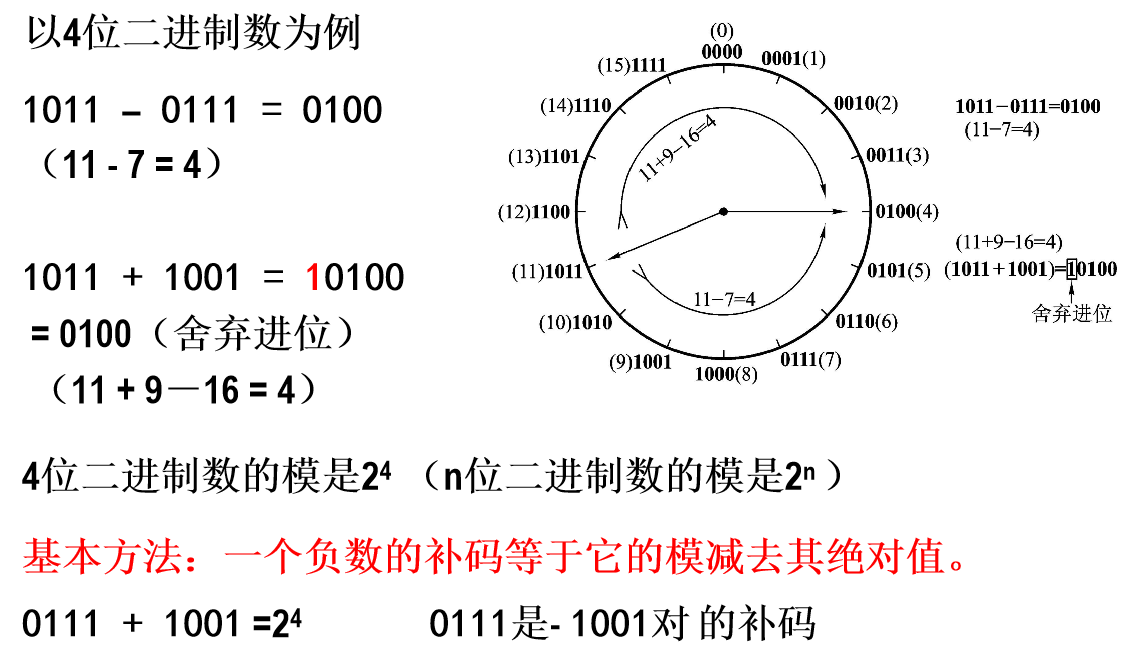
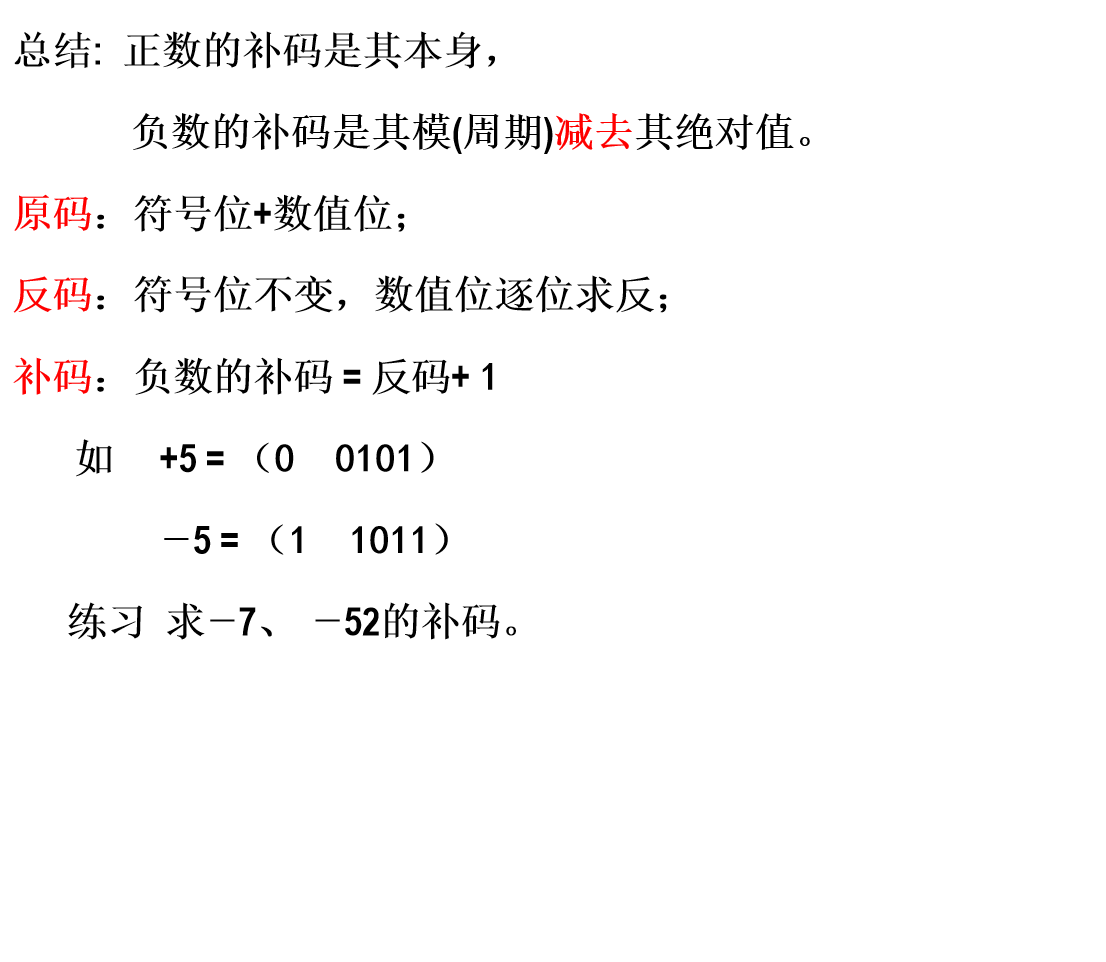
1.4.3 二进制数加减运算规则