刷题训练之二分查找

> 作者：დ旧言~
> 座右铭：松树千年终是朽，槿花一日自为荣。

> 目标：熟练掌握二分查找算法

> 毒鸡汤：学习，学习，再学习 ! 学，然后知不足。

> 专栏选自：刷题训练营

> 望小伙伴们点赞👍收藏✨加关注哟💕💕 

🌟前言分析

        最早博主续写了牛客网130道题，这块的刷题是让同学们快速进入C语言，而我们学习c++已经有一段时间了，知识储备已经足够了但缺少了实战，面对这块短板博主续写刷题训练，针对性学习，把相似的题目归类，系统的刷题，而我们刷题的官网可以参考：​​​​​​

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

而今天我们的板块是二分查找。

⭐知识讲解

很多小伙伴们在想二分查找嘛，只有升序或者是降序的数字里面查找，有这个想法的是大错特错的，在一些题目中有些无序也可以使用二分查找，所以说二分查找的知识点没有我们想的那么简单，在二分查找中我们会总结一些模板，这些模板要死记硬背要理解哦，题目选取的很多，大家不要跳过一些题目，有些题目是为后面的题目做铺垫的，望大家可以从头看到尾，这里就简单的总结一些二分查找的知识点：

  • 二分查找的时间复杂度：log(N)
  • 二分查找的范围：有序的数组或者无序

⭐经典题型

 🌙topic-->1

题目链接：1. 二分查找 - 力扣（LeetCode）

 

题目分析：

 在一个有序的数组中查找一个数字  target  ，如果存在就返回数组的下标，没有的话就返回-1

算法原理：

  • 解法一：

暴力遍历数组，时间复杂度为O(n)。

  • 解法二：

采用二分查找，二分算法原理博客，这里如果不会二分查找的小伙伴们大家可以看看这篇博客，这里我们再讲解一下解法二的算法原理。

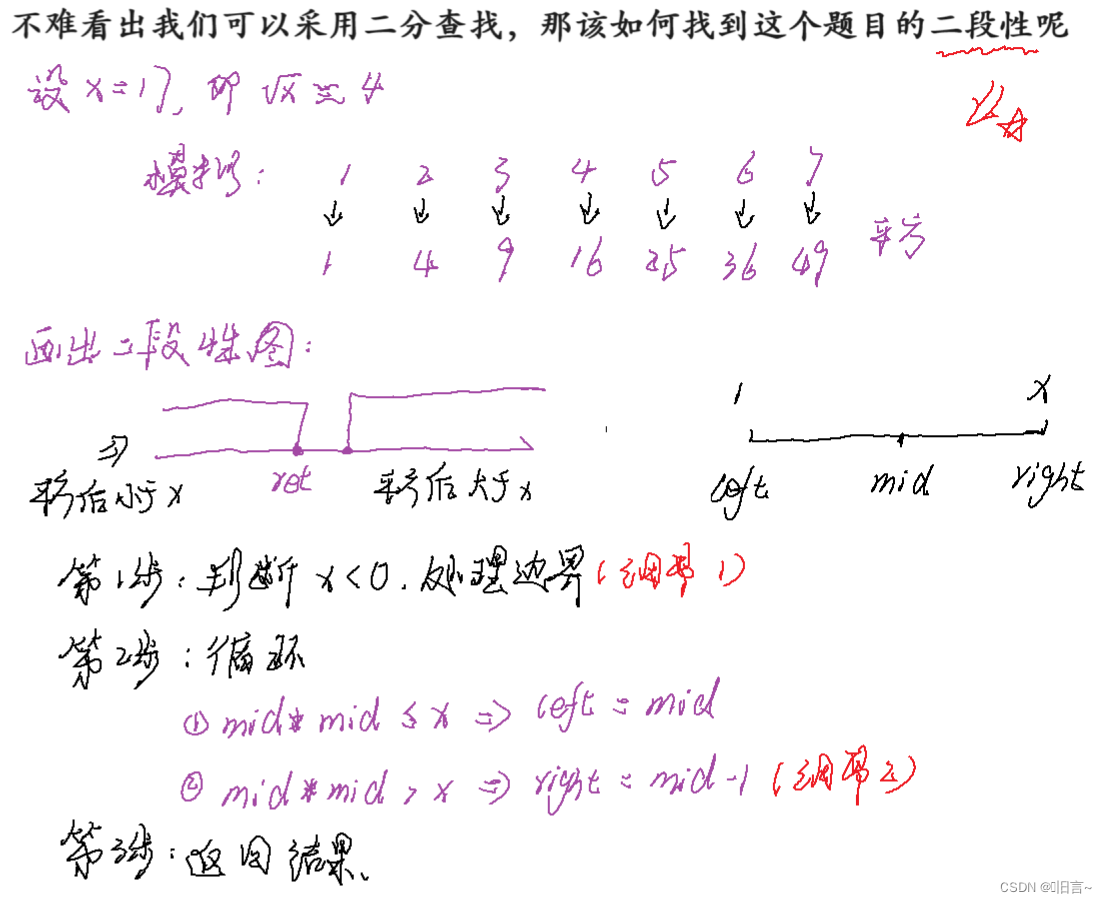
图解：

细节：

  1. 防止 mid 超过整形最大值
  2. 循环的条件是 left <= right

代码演示：

class Solution {
public:int search(vector<int>& nums, int target) {// 定义左右指针int left = 0,right = nums.size() - 1;// 循环while(left <= right) // 细节二{int mid = left + (right - left) / 2;// 细节一if(nums[mid] < target)left = mid + 1;else if(nums[mid] > target)right = mid - 1;elsereturn mid;}// 没有返回-1return -1;}
};

 模板总结：

// 定义左右指针int left = 0,right = nums.size() - 1;// 循环while(left <= right) // 细节二{// int mid = left + (right - left + 1) / 2 等价int mid = left + (right - left) / 2;// 细节一if(....)left = mid + 1;else if(....)right = mid - 1;elsereturn ...;}

🌙topic-->2

题目链接：2.二分查找力扣（LeetCode）

题目分析：

在一个非递归中找一个等于 target 下标，如果没有就返回 {-1，-1}

算法原理：

  • 解法一：

暴力遍历数组，时间复杂度为O(n)。

  • 解法二：

采用二分查找，二分算法原理博客，这里如果不会二分查找的小伙伴们大家可以看看这篇博客，这里我们再讲解一下解法二的算法原理。

代码演示：

class Solution
{
public:vector<int> searchRange(vector<int>& nums, int target){// 定义左右指针int left = 0,right = nums.size() - 1;// 处理空数组if(nums.size() == 0)return {-1,-1};int begin = 0;// 定义左边界// 去除左边界的元素while(left < right) // 细节一{int mid = left + (right - left) / 2;if(nums[mid] < target)left = mid + 1;// 细节二elseright = mid; }// 判断是否有值if(nums[left] != target)return {-1,-1};else begin = left;//标记左边界// 去除右边界left = 0,right = nums.size() - 1;while(left < right){int mid = left + (right - left + 1) / 2; // 细节if(nums[mid] <= target)left = mid;// 细节三elseright = mid - 1;// 细节四 }// 返回return {begin,right};}};

 模板总结：

while(left < right)
{int mid = left + (right - left) / 2;if(...) left = mid + 1;else right = mid;
}while(left < right)
{int mid = left + (right - left + 1) / 2;if(...) left = mid;else right = mid - 1;
}// 下面出现 -1 的时候，上面就加 +1

🌙topic-->3

这道题目就不再讲解的这么细了，具体还得琢磨第二道题目：

题目链接：3.二分查找  - 力扣（LeetCode）

题目分析：

给定一个排序数组（升序）和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

算法原理：

  • 解法一：

暴力遍历数组，时间复杂度为O(n)。

  • 解法二：

采用二分查找，二分算法原理博客，这里如果不会二分查找的小伙伴们大家可以看看这篇博客，这里我们再讲解一下解法二的算法原理。

代码演示：

class Solution {
public:int searchInsert(vector<int>& nums, int target) {// 定两个指针int left = 0,right = nums.size() - 1;// 循环while(left < right){int mid = left + (right - left) / 2;if(nums[mid] < target) left = mid + 1;else right = mid;}// 判断if(nums[left] < target)return right + 1;return right;}
};

 🌙topic-->4

这道题目就不再讲解的这么细了，具体还得琢磨第二道题目：

题目链接：4.二分查找  - 力扣（LeetCode）

 

题目分析：

求 X 的算数平方根，结果保留整数。

算法原理：

  • 解法一：

暴力举例1 2 3 .... x，时间复杂度为O(n)。

  • 解法二：

采用二分查找，二分算法原理博客，这里如果不会二分查找的小伙伴们大家可以看看这篇博客，这里我们再讲解一下解法二的算法原理。

代码演示：

class Solution {
public:int mySqrt(int x) {// 处理if(x < 1) return 0;// 定义两个指针int left = 1,right = x;// 循环while(left <right){// 防止溢出long long mid = left + (right - left +1) /2;if(mid * mid <= x) left = mid;else right = mid -1;}return left;}
};

  🌙topic-->5

这道题目就不再讲解的这么细了，具体还得琢磨第二道题目：

题目链接：5.二分查找  - 力扣（LeetCode）

  

题目分析：

有一个山峰数组（数组有递增和递减），返回数组中峰顶的下标。

算法原理：

  • 解法一：

暴力遍历数组就可以了，时间复杂度为O(n)。

  • 解法二：

采用二分查找，二分算法原理博客，这里如果不会二分查找的小伙伴们大家可以看看这篇博客，这里我们再讲解一下解法二的算法原理。

代码演示：

class Solution {
public:int peakIndexInMountainArray(vector<int>& arr) {// 定义两个指针int left = 1,right = arr.size() - 2;// 循环while(left < right){int mid = left + (right - left + 1) / 2;if(arr[mid] > arr[mid - 1]) left = mid;else right = mid - 1;}return left;}
};

   🌙topic-->6

这道题目就不再讲解的这么细了，这里和第五道题目几乎一样：

题目链接：6.二分查找  - 力扣（LeetCode）

  

题目分析：

有一个山峰数组，这个山峰数组有多个山峰，只要返回其中一峰顶就行（返回数组中峰顶的下标）

算法原理：

  • 解法一：

暴力遍历数组就可以了，时间复杂度为O(n)。

  • 解法二：

采用二分查找，二分算法原理博客，这里如果不会二分查找的小伙伴们大家可以看看这篇博客，这里我们再讲解一下解法二的算法原理。

代码演示：

class Solution {
public:int findPeakElement(vector<int>& nums) {// 定义两个指针int left = 0,right = nums.size() - 1;// 循环while(left < right){int mid = left + (right - left) / 2;if(nums[mid] < nums[mid + 1]) left = mid + 1;else right = mid;}return left;}
};

   🌙topic-->7

这道题目就不再讲解的这么细了，具体还得琢磨第二道题目：

题目链接：7. 二分查找- 力扣（LeetCode）

  

题目分析：

在一个数组中找最小值。

算法原理：

  • 解法一：

暴力遍历数组就可以了，时间复杂度为O(n)。

  • 解法二：

采用二分查找，二分算法原理博客，这里如果不会二分查找的小伙伴们大家可以看看这篇博客，这里我们再讲解一下解法二的算法原理。

代码演示：

class Solution
{
public:int findMin(vector<int>& nums){int left = 0, right = nums.size() - 1;int x = nums[right]; // 标记⼀下最后⼀个位置的值while (left < right){int mid = left + (right - left) / 2;if (nums[mid] > x) left = mid + 1;else right = mid;}return nums[left];}
};

 🌙topic-->8

这道题目就不再讲解的这么细了，具体还得琢磨第二道题目：

题目链接：8.二分查找  - 力扣（LeetCode）

  

题目分析：

在一个  0 ~  n-1  数组中找缺少的数字。

算法原理：

  • 解法一：

暴力遍历数组就可以了，时间复杂度为O(n)。

  • 解法二：

采用二分查找，二分算法原理博客，这里如果不会二分查找的小伙伴们大家可以看看这篇博客，这里我们再讲解一下解法二的算法原理。

代码演示：

class Solution {
public:int takeAttendance(vector<int>& records) {int missingNumber(vector<int>&nums){int left = 0, right = nums.size() - 1;while (left < right){int mid = left + (right - left) / 2;if (nums[mid] == mid) left = mid + 1;else right = mid;}return left == nums[left] ? left + 1 : left;}}
};

 🌟结束语

       今天内容就到这里啦，时间过得很快，大家沉下心来好好学习，会有一定的收获的，大家多多坚持，嘻嘻，成功路上注定孤独，因为坚持的人不多。那请大家举起自己的小手给博主一键三连，有你们的支持是我最大的动力💞💞💞，回见。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/642077.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

MLLM | Mini-Gemini: 挖掘多模态视觉语言大模型的潜力

MLLM | Mini-Gemini: 挖掘多模态视觉语言大模型的潜力

香港中文、SmartMore 论文标题&#xff1a;Mini-Gemini: Mining the Potential of Multi-modality Vision Language Models Code and models are available at https://github.com/dvlab-research/MiniGemini 一、问题提出 通过更高分辨率的图像增加视觉标记的数量可以丰富…
阅读更多...
Rust 认识所有权

Rust 认识所有权

目录 什么是所有权？ 栈（Stack）与堆（Heap）所有权规则变量作用域String 类型内存与分配 变量与数据交互的方式（一）：移动变量与数据交互的方式（二）：克隆只在栈上的数据：拷贝所有权与函数返回值与作用域引用与借用 可变引用悬垂引用（Dangling References）引用的规则S…
阅读更多...
众筹商城源码 众筹商品平台 商城加共识元富之路 网上商城众筹，附带系统搭建教程

众筹商城源码 众筹商品平台 商城加共识元富之路 网上商城众筹，附带系统搭建教程

前端是编译后的&#xff0c;后端PHP&#xff0c;带商城 全局替换http://dami.5288tj.com为你的域名 /MbedAdminentersdfsdrwe.php/index/login 账号&#xff1a;admin 密码;admin888 源码免费下载地址抄笔记 (chaobiji.cn)https://chaobiji.cn/
阅读更多...
谷歌（语法）搜索基本指令分享

谷歌（语法）搜索基本指令分享

1.site指令 *查询网站被搜索引擎的收录量 "限走搜索的范围是在某个特定的网站或域名下 *限走网站的类型&#xff0c;eg:.com/.us/.fr/.cn/.gov 1.site域名&#xff0c;eg:site:123456.com(主域名&#xff0c;一级域名)&#xff0c;eg:site:123456.com(二级域名)级域名网页…
阅读更多...
B203-若依框架应用

B203-若依框架应用

目录 简介版本RuoYi-fast项目准备新增模块/代码生成 简介 基于SpringBoot的权限管理系统&#xff0c;基于SpringBoot开发的轻量级Java快速开发框架 版本 前后端未分离单应用版本&#xff1a;RuoYi-fast&#xff0c;前后端未分离多模块版本&#xff1a;RuoYi 前后端分离单应用…
阅读更多...
3D视觉技术引领活塞杆抓取新革命

3D视觉技术引领活塞杆抓取新革命

随着工业自动化的快速发展&#xff0c;对高精度、高效率的抓取技术需求日益增长。活塞杆作为重要的机械零部件&#xff0c;其抓取过程的精确性直接关系到产品质量和生产效率。近年来&#xff0c;3D视觉技术以其独特的优势&#xff0c;在活塞杆抓取领域展现出巨大的应用潜力。 …
阅读更多...
【行为型模式】中介者模式

【行为型模式】中介者模式

一、中介者模式概述 中介者模式定义&#xff1a;用一个中介对象来封装一系列的对象交互&#xff0c;中介者使各对象不需要显式地相互引用&#xff0c;从而使其耦合松散&#xff0c;而且可以独立地改变它们之间的交互。中介者模式又称为调停者模式。(对象行为型模式) 中介者模式…
阅读更多...
STM32F407,429参考手册（中文）

STM32F407,429参考手册（中文）

发布一个适用STM32F405XX、STM32F407XX、STM32F415XX、STM32F417XX、STM32F427XX、STM32F437XX的中文数据手册&#xff0c;具体内容见下图&#xff1a; 点击下载&#xff08;提取码&#xff1a;spnn&#xff09; 链接: https://pan.baidu.com/s/1zqjKFdSV8PnHAHWLYPGyUA 提取码…
阅读更多...
ICC2：自动摆port的命令

ICC2：自动摆port的命令

我正在「拾陆楼」和朋友们讨论有趣的话题&#xff0c;你⼀起来吧&#xff1f; 拾陆楼知识星球入口 ICC2中可以通过命令去实现自动摆port&#xff0c;示例如下: set_individual_pin_constraints -ports $ports -allowed_layers M6 -sides 1 -pin_spacing_distance 1 这里需要…
阅读更多...
win11不能新建.txt文件？试试这个方法。

win11不能新建.txt文件？试试这个方法。

检查你的系统是否有notepad程序。 查看“开始”菜单中是否有“记事本”这个程序。如果没有&#xff0c;就去“Microsoft store”中下载一个“windows notepad”安装上。 如果有notepad&#xff0c;还是无法新建.txt文件&#xff0c;就需要设置注册表了。 键盘输入“winR”&…
阅读更多...
windows服务器被限制ping解除方式（防火墙被打开的情况）

windows服务器被限制ping解除方式（防火墙被打开的情况）

启用红框中的回显规则即可&#xff1a;
阅读更多...
STM32 ADC转换器

STM32 ADC转换器

一、ADC简介 ADC&#xff08;Analog-Digital Converter&#xff0c;模拟-数字转换器&#xff09;&#xff0c;可以将引脚上连续变化的模拟量转换为内存中存储的数字量&#xff0c;建立模拟电路到数字电路的桥梁 模拟量&#xff1a;时间和幅值均连续的信号&#xff0c;例如&…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023