分清楚三个量的含义和计算方法。
梯度
表征的是一个列向量,是相对于某个方向而言的,但是某个方向上可能有多个变量,所以梯度不是简单的直接求偏导,并且说了,它是一个列向量,所以,
我们设 f : F f:F f:F是 R n R^n Rn-> R R R的一阶连续可微函数,则 f f f在 x x x处的一阶偏导数:
∇ \nabla ∇ f ( x ) f(x) f(x)=( ∂ f ( x ) ∂ x 1 \frac{\partial f(x)}{\partial x_1} ∂x1∂f(x), ∂ f ( x ) ∂ x 1 \frac{\partial f(x)}{\partial x_1} ∂x1∂f(x), ⋯ \cdots ⋯, ∂ f ( x ) ∂ x n \frac{\partial f(x)}{\partial x_n} ∂xn∂f(x)) T ^T T
即:
∇ f ( x ) = ( ∂ f ( x ) ∂ x 1 ∂ f ( x ) ∂ x 2 ⋮ ∂ f ( x ) ∂ x n ) \nabla{f(x)}=\left(\begin{matrix}\frac{\partial f(x)}{\partial x_1} \\ \frac{\partial f(x)}{\partial x_2} \\ \vdots \\ \frac{\partial f(x)}{\partial x_n} \end{matrix} \right) ∇f(x)= ∂x1∂f(x)∂x2∂f(x)⋮∂xn∂f(x)
所以说是一个 R n − > R R_n->R Rn−>R的变换
hesse阵
在梯度的基础上就是二阶偏导就是hesse阵,注意由于是二阶偏导,所以不止是平方,还有混合偏导数的存在。
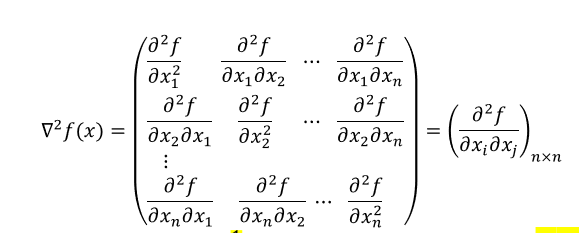
∇ 2 f ( x ) \nabla^2{f(x)} ∇2f(x)=( ∂ 2 f ∂ x i ∂ x j ) n × n \frac{\partial^2{f}}{\partial{x_i}\partial{x_j}})_{n\times n} ∂xi∂xj∂2f)n×n
∇ 2 f ( x ) = ( ∂ 2 f ∂ x 1 2 ∂ 2 f ∂ x 1 ∂ x 2 ⋯ ∂ 2 f ∂ x 1 ∂ x n ∂ 2 f ∂ x 2 ∂ x 1 ∂ 2 f ∂ x 2 2 ⋯ ∂ 2 f ∂ x 2 ∂ x n ⋮ ∂ 2 f ∂ x n ∂ x 1 ∂ 2 f ∂ x n ∂ x 2 ⋯ ∂ 2 f ∂ x n 2 ) \nabla^2f(x)=\left(\begin{matrix} \frac{\partial^2f}{\partial x_1^2} \frac {\partial^2f}{\partial x_1\partial x_2} \cdots \frac{\partial^2f}{\partial x_1\partial x_n} \\ \frac{\partial^2f}{\partial x_2 \partial x_1} \frac{\partial^2f}{\partial x_2^2} \cdots \frac{\partial^2f}{\partial x_2 \partial x_n} \\ \vdots \\ \frac{\partial^2f}{\partial x_n \partial x_1} \frac{\partial^2f}{\partial x_n \partial x_2} \cdots \frac{\partial^2f}{\partial x_n^2} \end{matrix} \right) ∇2f(x)= ∂x12∂2f∂x1∂x2∂2f⋯∂x1∂xn∂2f∂x2∂x1∂2f∂x22∂2f⋯∂x2∂xn∂2f⋮∂xn∂x1∂2f∂xn∂x2∂2f⋯∂xn2∂2f
每一行都已 x i x_i xi开始,然后求二阶继续从 x i x_i xi到 x n x_n xn求出
雅可比
其实是一种维度拓宽的梯度的表示方法,也就是 f f f是 F ⊆ R n → R m F\subseteq{R^n}\rightarrow{R^m} F⊆Rn→Rm, x x x在F上连续可微,则一阶导数为:
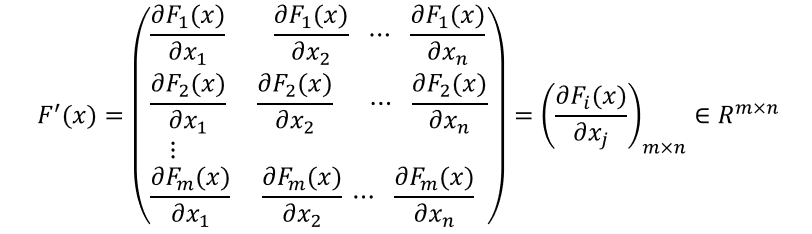
F ′ ( x ) = ( ∂ F i ( x ) ∂ x j ) m × n ∈ R m × n F'(x)=(\frac{\partial{F_i(x)}}{\partial{x_j}})_{m\times n}\in{R^{m\times n}} F′(x)=(∂xj∂Fi(x))m×n∈Rm×n
也就是说,向量值函数的导数就是雅可比矩阵,向量中的每一项分别求梯度再组合起来。
比如:对于 f : R n → R f:R^n \rightarrow R f:Rn→R
我们可以和梯度以及hesse阵联系起来看Jacobi矩阵,
H ( x ) = J ( ∇ f ( x ) ) H(x)=J(\nabla f(x)) H(x)=J(∇f(x))
H ( x ) = ∇ 2 f ( x ) H(x)=\nabla^2f(x) H(x)=∇2f(x)
梯度的Jacobi矩阵就是hesse阵。
举个例子说明一下:
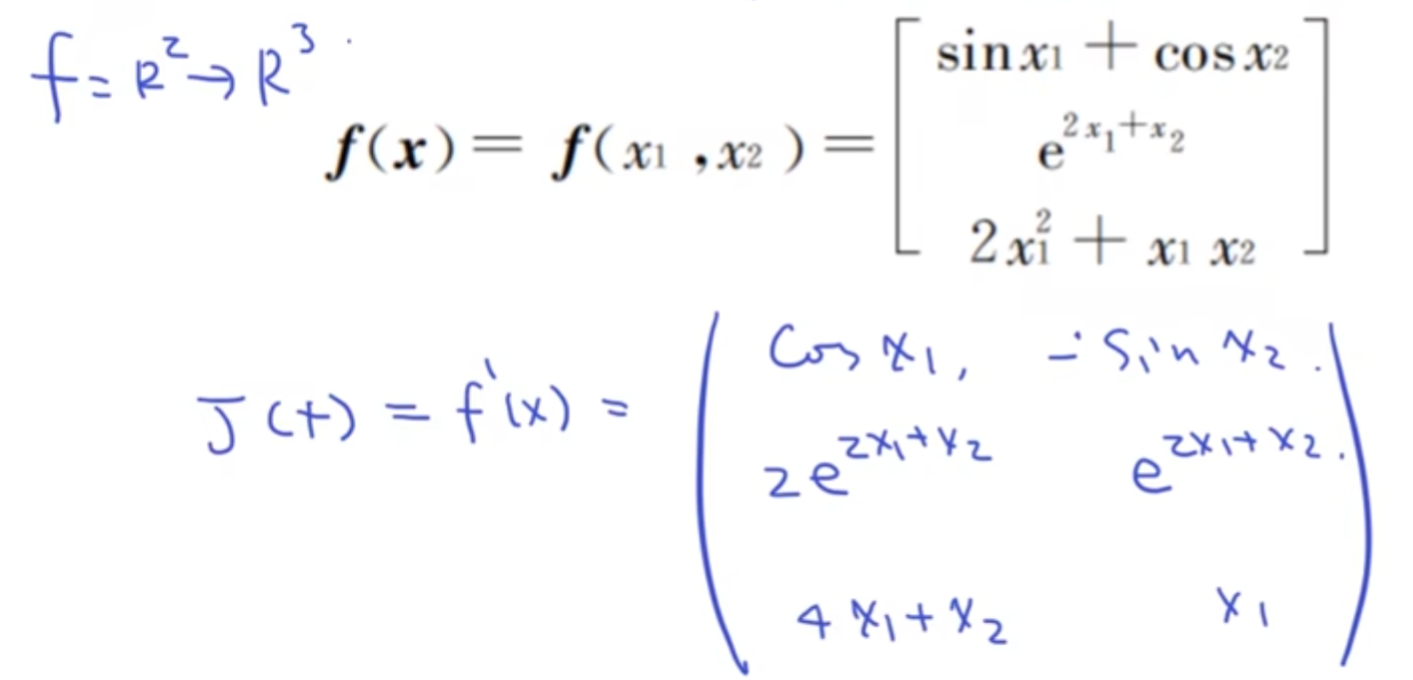
以上用到的markdown语法
分数 x y \frac{x}{y} yx \frac{x}{y}
偏导数 ∂ f ( x ) \partial{f(x)} ∂f(x) \partial{f(x)}
梯度 ∇ f ( x ) \nabla{f(x)} ∇f(x) \nabla{f(x)}
表示x_1^2的: x i j x_i^j xij
×:\times
vdots
cdots
\leftarrow
\rightarrow
\in 属于
⊆ \subseteq ⊆ 包含 \subseteq