Crocoddyl 使用教程（二）-编程知识

系列文章目录

前言

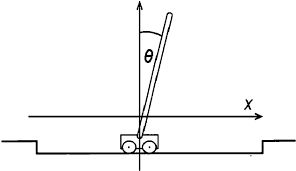
小车摆杆是另一个经典的控制实例。在这个系统中，一根欠驱动的杆子被固定在一辆一维驱动的小车顶部。游戏的目的是将杆子升到站立位置。

模型如下： https://en.wikipedia.org/wiki/Inverted_pendulum

我们用 $m_1$ 表示小车质量、 $m_2$ 表示摆杆质量 ( $m=m_1+m_2$ )、 $l$ 表示摆杆长度、 $\theta$ 表示摆杆相对于垂直轴的角度、 $p$ 表示小车位置、 $g=9.81$ 表示重力。

系统加速度可重写为

$\ddot{\theta}=\dfrac1{\mu(\theta)}\big(\dfrac{\cos\theta}lf+\dfrac{mg}l\sin(\theta)-m_2\cos(\theta)\sin(\theta)\dot{\theta}^2\big),\\\ddot{p}=\dfrac1{\mu(\theta)}\big(f+m_2\cos(\theta)\sin(\theta)g-m_2l\sin(\theta)\dot{\theta}\big),$

其中，

$\mu(\theta)=m_1+m_2\sin(\theta)^2,$

其中， $f$ 代表输入指令（即 $f=u$ ）， $m=m_1+m_2$ 代表总质量。

一、微分动作模型

微分动作模型（DAM）描述的是连续时间内的动作（控制/动力学）。在本练习中，我们要求您编写小车摆杆的运动方程。

更多详情，请参阅 DifferentialActionModelCartpole 类中的说明。

import crocoddyl
import pinocchio
import numpy as np
from IPython.display import HTML
from cartpole_utils import animateCartpoleclass DifferentialActionModelCartpole(crocoddyl.DifferentialActionModelAbstract):def __init__(self):crocoddyl.DifferentialActionModelAbstract.__init__(self, crocoddyl.StateVector(4), 1, 6)  # nu = 1; nr = 6self.unone = np.zeros(self.nu)self.m1 = 1.0self.m2 = 0.1self.l = 0.5self.g = 9.81self.costWeights = [1.0,1.0,0.1,0.001,0.001,1.0,]  # sin, 1-cos, x, xdot, thdot, fdef calc(self, data, x, u=None):if u is None:u = model.unone# Getting the state and control variablesy, th, ydot, thdot = x[0].item(), x[1].item(), x[2].item(), x[3].item()f = u[0].item()# Shortname for system parametersm1, m2, l, g = self.m1, self.m2, self.l, self.gs, c = np.sin(th), np.cos(th)####################################################################################### TODO: Write the dynamics equation of your system ######################################################################################### Hint:# You don't need to implement integration rules for your dynamic system.# Remember that DAM implemented action models in continuous-time.m = m1 + m2mu = m1 + m2 * s**2xddot, thddot = cartpole_dynamics(self, data, x, u)  # Write the cartpole dynamics heredata.xout = np.matrix([xddot, thddot]).T# Computing the cost residual and valuedata.r = np.matrix(self.costWeights * np.array([s, 1 - c, y, ydot, thdot, f])).Tdata.cost = 0.5 * sum(np.asarray(data.r) ** 2).item()def calcDiff(model, data, x, u=None):# Advance user might implement the derivatives in cartpole_analytical_derivativescartpole_analytical_derivatives(model, data, x, u)

取消下面一行的注释，就能得到小车摆杆动力学的解：

# %load solutions/cartpole_dyn.py

您可能需要检查一下您的计算结果。以下是创建模型和运行计算方法的方法。

cartpoleDAM = DifferentialActionModelCartpole()
cartpoleData = cartpoleDAM.createData()
x = cartpoleDAM.state.rand()
u = np.zeros(1)
cartpoleDAM.calc(cartpoleData, x, u)

二、使用 DAMNumDiff 写导数

在前面的练习中，我们没有定义 cartpole 系统的导数。在 crocoddyl 中，我们可以利用 DifferentialActionModelNumDiff 类来计算导数，而无需任何额外代码。该类通过数值微分计算导数。

在下面的单元格中，您需要创建一个使用 NumDiff 计算导数的 cartpole DAM。

# Creating the carpole DAM using NumDiff for computing the derivatives.
# We specify the withGaussApprox=True to have approximation of the
# Hessian based on the Jacobian of the cost residuals.
cartpoleND = crocoddyl.DifferentialActionModelNumDiff(cartpoleDAM, True)

使用 NumDiff 创建 cartpole DAM 后。我们希望您能回答以下问题：

Fx 的 2 列为空。是 Wich 列吗？为什么？
能否仔细检查一下 Fu 的值？

# %load solutions/cartpole_fxfu.py

三、积分模型

为 cartpole 系统创建 DAM 后。我们需要创建一个积分动模型（IAM）。请注意，IAM 将连续时间动作模型转换为离散时间动作模型。在本练习中，我们将使用简单欧拉积分器。

# %load solutions/cartpole_integration.py
###########################################################################
################## TODO: Create an IAM with from the DAM ##################
###########################################################################
# Hint:
# Use IntegratedActionModelEuler

四、编写问题，创建求解器

首先，您需要描述射击问题。为此，您必须说明步的数量及其时间步长。在本练习中，我们希望使用 50 步和 5e-2。

下面是我们创建问题的方法。

# Fill the number of knots (T) and the time step (dt)
x0 = np.array([0.0, 3.14, 0.0, 0.0])
T = 50
problem = crocoddyl.ShootingProblem(x0, [cartpoleIAM] * T, cartpoleIAM)

问题不能解决，只能积分：

us = [np.zeros(cartpoleIAM.differential.nu)] * T
xs = problem.rollout(us)

在 cartpole_utils 中，我们提供了 plotCartpole 和 animateCartpole 方法。让我们展示一下这个滚动条！

请注意，to_jshtml 会生成视频控制命令。

HTML(animateCartpole(xs).to_jshtml())

# %load solutions/cartpole_ddp.py
# #########################################################################
# ################# TODO: Create the DDP solver and run it ###############
# ##########################################################################

HTML(animateCartpole(ddp.xs.tolist()).to_jshtml())

五、调整问题，解决问题

指出解决问题的方法。

没有终端模型，我们可以看到一些波动，但无法稳定下来。怎么办？
最重要的是达到站立位置。我们还能使速度失效吗？
增加所有权重是行不通的。如何慢慢增加惩罚？

# %load solutions/cartpole_tuning.py
# ##########################################################################
# ################# TODO: Tune the weights for each cost ###################
# ##########################################################################
terminalCartpole = DifferentialActionModelCartpole()
terminalCartpoleDAM = crocoddyl.DifferentialActionModelNumDiff(terminalCartpole, True)
terminalCartpoleIAM = crocoddyl.IntegratedActionModelEuler(terminalCartpoleDAM)terminalCartpole.costWeights[0] = 0  # fix me :)
terminalCartpole.costWeights[1] = 0  # fix me :)
terminalCartpole.costWeights[2] = 0  # fix me :)
terminalCartpole.costWeights[3] = 0  # fix me :)
terminalCartpole.costWeights[4] = 0  # fix me :)
terminalCartpole.costWeights[5] = 0  # fix me :)
problem = crocoddyl.ShootingProblem(x0, [cartpoleIAM] * T, terminalCartpoleIAM)

# Creating the DDP solver
ddp = crocoddyl.SolverDDP(problem)
ddp.setCallbacks([crocoddyl.CallbackVerbose()])# Solving this problem
done = ddp.solve([], [], 300)
print(done)

HTML(animateCartpole(ddp.xs.tolist()).to_jshtml())

六、使用分析导数

取消下面一行的注释，就能得到分析导数的解：

# %load solutions/cartpole_analytical_derivatives.py
def cartpole_analytical_derivatives(model, data, x, u=None):pass

在定义了分析导数后，我们就不需要使用 DAMNumDiff 对导数进行数值逼近了。

timeStep = 5e-2
cartpoleIAM = crocoddyl.IntegratedActionModelEuler(cartpoleDAM, timeStep)

现在您可以再次运行 "IV. 编写问题，创建求解器 "中的所有模块，因为 cartpoleIAM 已被重新定义为直接使用解析导数。