FollowUp
1.插入排序
(1).直接插入排序
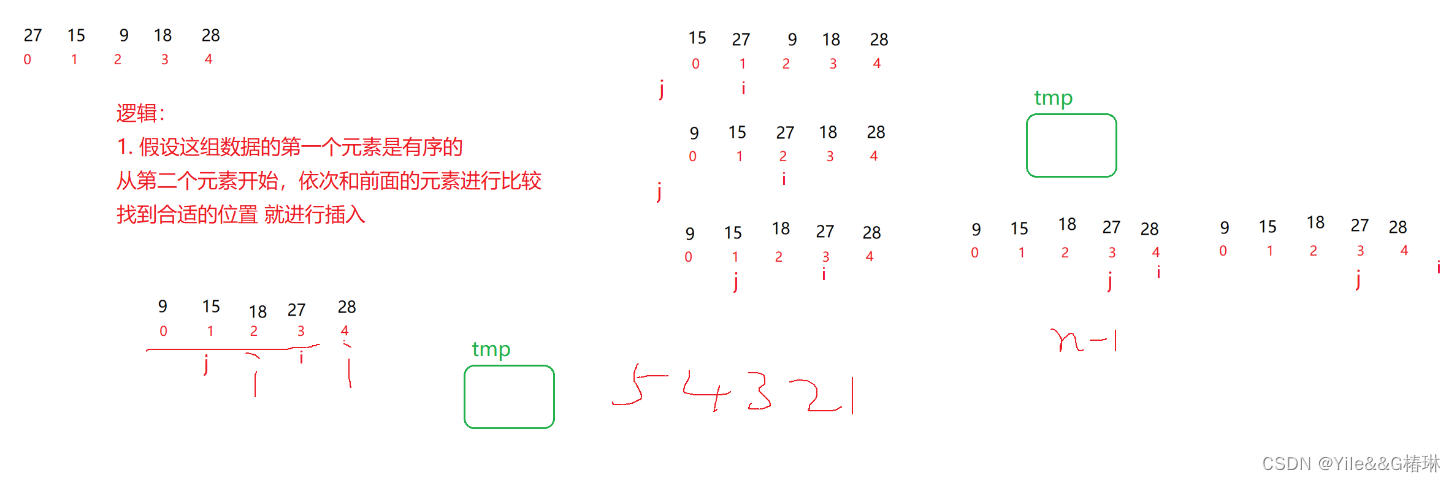
时间复杂度:
最坏情况下:0(n^2)
最好情况下:0(n)当数据越有序 排序越快适用于: 待排序序列 已经基本上趋于有序了!
空间复杂度:0(1)
稳定性:稳定的public static void insertSort(int[] array){for (int i = 1; i < array.length; i++) {int tmp = array[i];int j = i - 1;for (; j >= 0 ; j--) {//这里加不加等号 和稳定有关系// 但是:本身就是一个稳定的排序 可以实现为不稳定的排序// 但是 本身就是一个不稳定的排序 是不可能变成一个稳定的排序的if(array[j] > tmp){array[j + 1] = array[j];}else {break;}}array[j+1] = tmp;}}
(2).希尔排序(缩小增量排序)

 重点是最后还是会把整体作一组来直接插入排序
重点是最后还是会把整体作一组来直接插入排序

public static void shellSort(int[] array){int gap = array.length;while(gap > 1){shell(array,gap);gap /= 2;}}public static void shell(int[] array, int gap){for (int i = gap; i < array.length; i++) {int tmp = array[i];int j = i - gap;for (;j >= 0; j -= gap) {if(array[j] > tmp){array[j+gap] = array[j];}else {break;}}array[j+gap] = tmp;}}2.选择排序
(1).直接选择排序
在元素集合array[i]--array[n-1]中选择关键码最大(小)的数据元素
若它不是这组元素中的最后一个(第一个)元素,则将它与这组元素中的最后一个(第一个)元素交换
在剩余的array[i]--array[n-2](array[i+1]--array[n-1])集合中,重复上述步骤,直到集合剩余1个元素
public static void selectSort(int[] array){for (int i = 0; i < array.length; i++) {int mixIndex = i;for (int j = i+1; j < array.length; j++) {if(array[mixIndex] > array[j]){mixIndex = j;}}int tmp = array[i];array[i] = array[mixIndex];array[mixIndex] = tmp;}}【直接选择排序的特性总结】
1. 直接选择排序思考非常好理解,但是效率不是很好。实际中很少使用
2. 时间复杂度:O(N^2)
3. 空间复杂度:O(1)
4. 稳定性:不稳定
(2.)双向选择排序:
public static void selectSort2(int[] array){int left = 0;int right = array.length-1;while(left < right){int minIndex = left;int maxIndex = left;for (int i = left+1; i < right; i++) {if(array[i] > array[maxIndex]){maxIndex = i;}if(array[i] < array[minIndex]){minIndex = i;}swap(array,left,minIndex);//防止最大的是在第一个的时候if(maxIndex == left){maxIndex = minIndex;}swap(array,right,maxIndex);left++;right--;}}}
(3).堆排序
具体的思路在PriorityQueue(一)——用堆实现优先级队列
public static void heapSort(int[] array){creatHeap(array);int end = array.length-1;while(end > 0){swap(array,0,end);siftDown(array,0,end);end--;}}private static void creatHeap(int[] array) {for (int parent = (array.length-1-1)/2; parent >= 0 ; parent--) {siftDown(array,parent,array.length);}}private static void siftDown(int[] array,int parent,int len) {int child = 2*parent + 1;while(child < len){if(child +1 < len && array[child] < array[child+1]){child++;}if(array[child] > array[parent]){swap(array,child,parent);parent = child;child = 2*parent + 1;}else {break;}}} public static void swap(int[] array, int i, int j){int tmp = array[i];array[i] = array[j];array[j] = tmp;}
3.交换排序
(1).冒泡排序
优化:
时间复杂度:0(N^2)
如果加了优化:最好情况下 可以达到0(n)空间复杂度:0(1)
稳定性:稳定的排序
优化:每一趟都需要判断 上一趟 有没有交换public static void bubbleSort(int[] array){for (int i = 0; i < array.length-1; i++) {boolean flg = false;for (int j = 0; j < array.length -1 - i ; j++) {if(array[j] > array[j+1]){swap(array,j,j+1);flg =true;}}//说明上一趟没有交换,也就是有序了if(!flg){break;}}}public static void swap(int[] array, int i, int j){int tmp = array[i];array[i] = array[j];array[j] = tmp;}
(2).快速排序
时间复杂度
最好的情况下:0(N*logN) 最坏情况下:0(N^2)逆宇|有序空间复杂度:
最好的情况下:0(logN) 最坏情况下:0(N)逆序/有序
稳定性:不稳定
快排最好和最坏情况分析

Hoare法
记录下key L和R相向出发,R找比Key小的值,L找比Key大的值,R先找找到后,L再找,两个找到交换;直到L和R相遇,相遇的位置为最后L找到的小于Key的值(让R先找的原因),此时的L就是pivot ,将Key和L交换
然后以pivot为中点,将它左右两边的循环以上操作也就是递归直到传入的L和R为相同的,那么任何一个以pivot为中点的数组都变成有序的了
pivot指的是l和r相遇的位置

public static void quickSort(int[] array){quick(array,0, array.length-1);}private static void quick(int[] array,int start,int end) {if(start >= end){return;}int pivot = partitionHoare(array,start,end);quick(array,start,pivot-1);quick(array,pivot+1,end);}private static int partitionHoare(int[] array, int left, int right) {int tmp = array[left];int i = left;while(left < right){while(left < right && array[right] >= tmp){right--;}while (left < right && array[left] <= tmp){left++;}swap(array,left,right);}swap(array,i,left);return left;}总结:
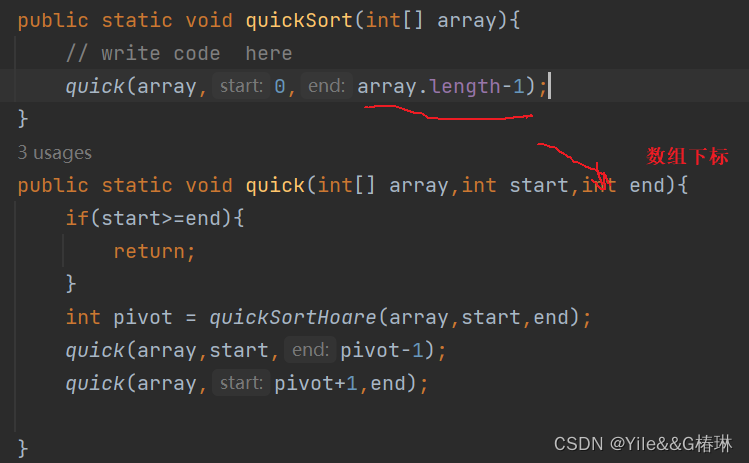
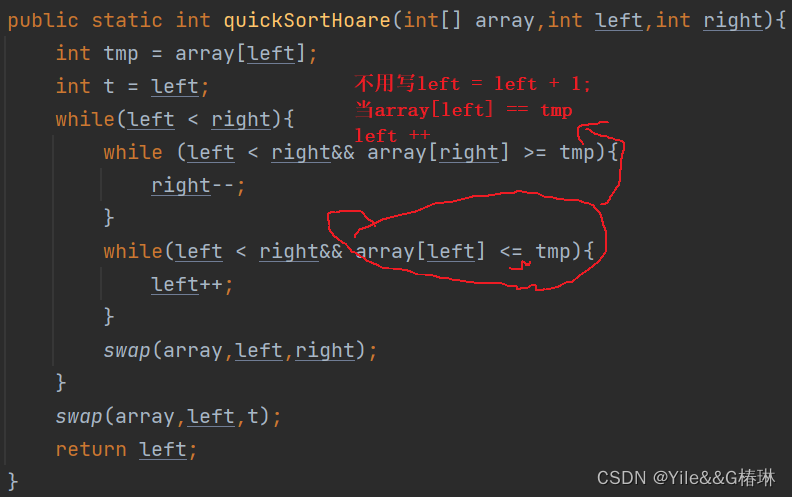
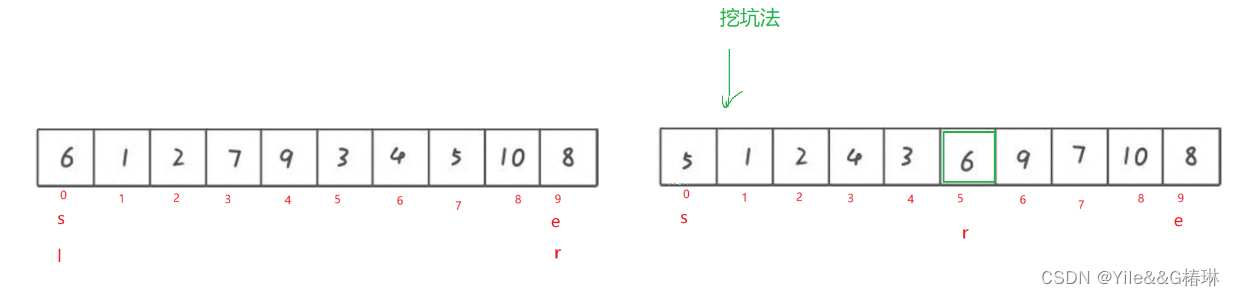
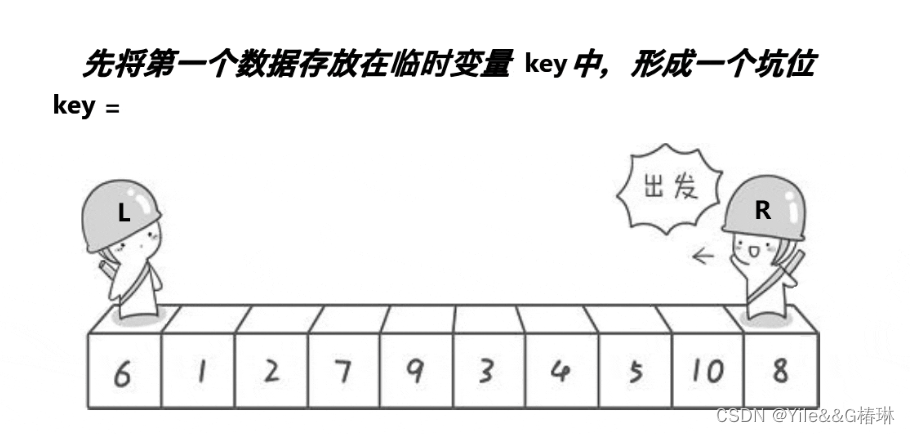
挖坑法
向将L的第一个位置为key,也就是坑位置,然后还是R先走找到比key小的就将R下标的值给坑位,此时R为坑位,L再走,找到比L大的值,放到坑位,L此时变为坑位,直到R和L相遇,还是保证L和R相遇的时候,是R找的比Key小的放到坑位里,然后将相遇的坑位放入Key
public static void quickSort(int[] array){quick(array,0, array.length-1);}private static void quick(int[] array,int start,int end) {if(start >= end){return;}int pivot = partitionHole(array,start,end);quick(array,start,pivot-1);quick(array,pivot+1,end);}private static int partitionHole(int[] array, int left, int right) {int tmp = array[left];int t = left;while(left < right){while(left < right && array[right] >= tmp){right--;}array[left] = array[right];while (left < right && array[left] <= tmp){left++;}array[right] = array[left];}array[left] = tmp;return left;}总结:

前后指针法
cur指向left加1的位置,prev指向left的位置,cur往前走,当遇到一个小于left下标值,并且此时cur和prev指向的不是同一个位置,那么cur和prev下标的值互换,直到cur超过right此时将prev和left下标的值互换,并返回prev,即是相对的中间位置
public static void quickSort(int[] array) {quick(array, 0, array.length - 1);}
public static int partition(int[] array, int left, int right){int prev = left;int cur = left + 1;while (cur <= right){if(array[cur] < array[left] && array[++prev] != array[cur]){swap(array,prev,cur);}cur++;}swap(array,left,prev);return prev;}private static void quick(int[] array,int start,int end) {if(start >= end){return;}if(end - start + 1 <= 15){insertSort(array,start,end);return;}int index = middleNume(array,start,end);swap(array,start,index);int pivot = partition(array,start,end);quick(array,start,pivot-1);quick(array,pivot+1,end);}
优化


public static void quickSort(int[] array){quick(array,0, array.length-1);}
private static void quick(int[] array,int start,int end) {if(start >= end){return;}if(end - start + 1 <= 15){insertSort(array,start,end);return;}int index = middleNume(array,start,end);swap(array,start,index);int pivot = partitionHoare(array,start,end);quick(array,start,pivot-1);quick(array,pivot+1,end);}private static int middleNume(int[] array, int left, int right) {int mid = (left + right)/2;if(array[left] < array[right] ){if(array[mid] < array[left]){return left;}else if(array[mid] > array[right]){return right;}else {return mid;}}else {if(array[mid] < array[right]){return right;}else if(array[mid] > array[left]){return left;}else {return mid;}}}public static void insertSort(int[] array,int left,int right){for (int i = left+1; i <= right; i++) {int tmp = array[i];int j = i - 1;for (; j >= left ; j--) {if(array[j] > tmp){array[j + 1] = array[j];}else {break;}}array[j+1] = tmp;}}非递归的方法

public static void quickSortNor(int[] array){int start = 0;int end = array.length -1;Stack<Integer> stack =new Stack<>();int pivot = partitionHoare(array,start,end);if(pivot - 1 > start){stack.push(start);stack.push(pivot-1);}if(pivot+1 < end){stack.push(pivot+1);stack.push(end);}while(!stack.empty()){end =stack.pop();start = stack.pop();pivot = partitionHoare(array,start,end);if(pivot - 1 > start){stack.push(start);stack.push(pivot-1);}if(pivot+1 < end){stack.push(pivot+1);stack.push(end);}}}private static int partitionHoare(int[] array, int left, int right) {int tmp = array[left];int i = left;while(left < right){while(left < right && array[right] >= tmp){right--;}while (left < right && array[left] <= tmp){left++;}swap(array,left,right);}swap(array,i,left);return left;}4. 归并排序
时间复杂度:0(N*logN)
空间复杂度:0(logN)
稳定性:稳定的
排序目前为止3个稳定的排序:直接插入排序、冒泡排序、归并排序
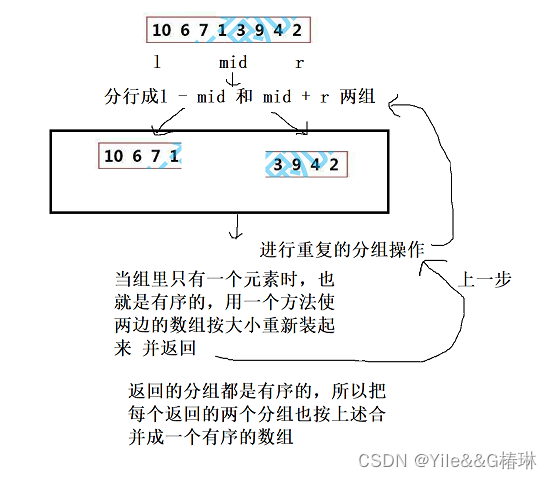

public static void mergeSort(int[] array){mergeSortFun(array,0,array.length-1);}public static void mergeSortFun(int[] array,int start,int end){if(start >= end){return;}int mid = (start + end)/2;mergeSortFun(array,start,mid);mergeSortFun(array,mid+1,end);//左右两边数组合并merge(array,start,mid,end);}public static void merge(int[] array,int left,int mid, int right){int s1 = left;int e1 = mid;int s2 = mid+1;int e2 = right;//两边的数组合并数组的长度int[] tmpArray = new int[right - left +1];int k = 0;while (s1 <= e1 && s2 <= e2){if(array[s1] < array[s2]){tmpArray[k++] = array[s1++];}else {tmpArray[k++] = array[s2++];}}while (s1 <= e1){tmpArray[k++] = array[s1++];}while (s2 <= e2){tmpArray[k++] = array[s2++];}for (int i = 0; i < tmpArray.length; i++) {array[left+i] = tmpArray[i];}}
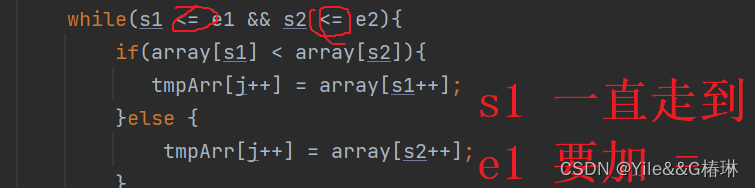
非递归

public static void merge(int[] array,int left,int mid, int right){int s1 = left;int e1 = mid;int s2 = mid+1;int e2 = right;//两边的数组合并数组的长度int[] tmpArray = new int[right - left +1];int k = 0;while (s1 <= e1 && s2 <= e2){if(array[s1] < array[s2]){tmpArray[k++] = array[s1++];}else {tmpArray[k++] = array[s2++];}}while (s1 <= e1){tmpArray[k++] = array[s1++];}while (s2 <= e2){tmpArray[k++] = array[s2++];}for (int i = 0; i < tmpArray.length; i++) {array[left+i] = tmpArray[i];}}public static void mergeSortNor(int[] array) {//每组几个数据int gap = 1;while(gap < array.length){for (int i = 0; i < array.length; i = i + gap*2) {int left = i;int mid = left + gap -1;int right = mid + gap;if(mid >= array.length){mid = array.length - 1;}if(right >= array.length){right = array.length - 1;}merge(array,left,mid,right);}gap = gap*2;}}5.非比较排序
 使用场景是给定一个指定的待排序的序列
使用场景是给定一个指定的待排序的序列
public static void countSort(int[] array){int minVal = array[0];int maxVal = array[0];for (int i = 0; i < array.length; i++){if(array[i] > maxVal){maxVal = array[i];}if(array[i] < minVal){minVal = array[i];}}int len = maxVal - minVal + 1;int[] count = new int[len];for (int i = 0; i < array.length; i++) {count[array[i]-minVal]++;}int index = 0;for (int i = 0; i < array.length; i++) {while(count[0] > 0){array[index] = i + minVal;index++;count[i]--;}}}海量数据的排序问题
外部排序:排序过程需要在磁盘等外部存储进行的排序
前提:内存只有 1G,需要排序的数据有 100G
因为内存中因为无法把所有数据全部放下,所以需要外部排序,而归并排序是最常用的外部排序
1. 先把文件切分成 200 份,每个 512 M
2. 分别对 512 M 排序,因为内存已经可以放的下,所以任意排序方式都可以
3. 进行 2路归并,同时对 200 份有序文件做归并过程,最终结果就有序了

记录当前电脑的时间
long startTime =System.currentTimeMillis();